Понятие неопределенного интеграла
Определение 2. Множество всех первообразных данной функции f (x) на интервале (a; b) называется неопределенным интегралом функции f(x) на этом интервале и обозначается символом:
В обозначении
Теорема 2. Если функция f (x) непрерывна на (a; b), то она имеет на (a; b) первообразную и неопределенный интеграл. Замечание. Операция нахождения неопределенного интеграла от данной функции f (x) на некотором промежутке носит название интегрирования функции f (x).
Свойства неопределенного интеграла. Из определений первообразной F (x) неопределенного интеграла от данной функции f (x) на некотором промежутке следуют свойства неопределенного интеграла: 1. 2. 3. 4. 5.
Замечание. Все вышеперечисленные свойства верны при условии. Что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.
Таблица основных неопределенных интегралов. Действие интегрирования является обратным действию дифференцирования, то есть по заданной производной f (x) надо восстановить начальную функцию F (x). Тогда из определения 2 и таблицы производных получается таблица основных интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. В формулах 1-16 С – произвольная постоянная. Замечание. Интеграл не от любой элементарной функции является элементарной функцией. Параметрами могут служить следующие интегралы, часто встречающиеся в задачах:
Указанные функции существуют, имеют важное прикладное значение. Для них составлены таблицы значений.
|


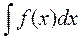 знак
знак  называется знаком интеграла,
называется знаком интеграла, 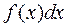 - подынтегральным выражением,
- подынтегральным выражением,  - подынтегральной функцией,
- подынтегральной функцией,  - переменной интегрирования.
- переменной интегрирования. .
.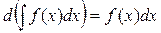 .
. , где С – произвольная постоянная.
, где С – произвольная постоянная. , где k = const.
, где k = const.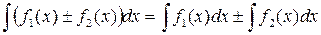
 .
. .
. .
. .
. .
. .
.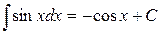 .
.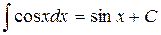 .
. .
. .
. .
.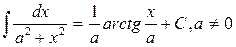 .
. .
. .
. .
. .
. - интеграл Пуассона,
- интеграл Пуассона, - интеграл Френеля,
- интеграл Френеля, - интегральный логарифм,
- интегральный логарифм,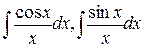
 - интегральный косинус и синус.
- интегральный косинус и синус.


