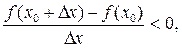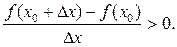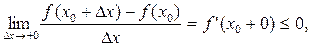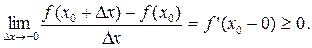Доказательство.

1) Для определенности рассмотрим случаи, когда функция y = f (x) в точке x ₀ имеет максимум и в этой точке существует производная. Тогда из определения максимума для любого x, принадлежащего окрестности точки x ₀ f (x ₀) > f (x).

Отсюда следует, что для любого D x # 0 справедливо неравенство: f (x ₀+D x) - f (x ₀) < 0. Разделим неравенство на D x. При этом получим:

при D x > 0:

при D x < 0:

 

Перейдем к пределам:

 

 

Так как f ”(x ₀) существует, то:

f ’(x ₀+0) = f ’(x ₀-0) = f (x ₀) = 0.

 

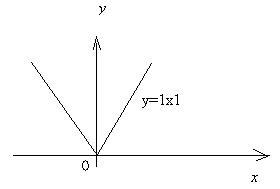
Аналогично рассматривается случай, когда x ₀ – точка минимума.

2) Если f ' (x ₀) не существует или равна ¥, то точка x ₀ может быть точкой экстремума функции.

Например, функция y = 1х1 имеет минимум при x = 0, хотя y ' (0) не существует (рис.9)

Рис. 9

 

Теорема доказана.

 

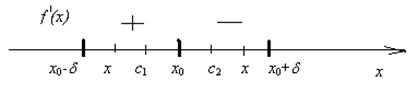
Теорема 4 (достаточное условие экстремума)

Если функция y = f (x) непрерывна в точке x ₀, дифференцируема в некоторой ее окрестности за исключением, может быть, самой этой точки, f ’(x ₀) = 0 или не существует и при переходе x через точку x ₀ f ’(x) изменяет знак, то точка x ₀ является точкой экстремума. Если при этом знак f ’(x) меняется.

с «+» на «-», то x ₀ - точка максимума,

с «-» на «+», то x ₀ - точка минимума.

Доказательство. Пусть f ’(x) при переходе x через точку x ₀ изменяет знак с «+» на «-», то есть f ’(x)>0 при x Î (x ₀-d; x ₀)

и f ’(x)<0 при x Î (x ₀; x ₀ +d), где d>0.

(рис.10).

Рис. 10

 

 

1) Пусть x Î (x ₀-d; x ₀). На отрезке [ x; x ₀] функция y = f (x) удовлетворяет теореме Лагранжа (по условию теоремы 4). Значит, на (x; x ₀) найдется хотя бы одна точка c₁, в которой выполняется равенство:

f (x) – f (x ₀) = f ’(c₁)×(x – x ₀), где c₁Î(x ₀-d; x ₀).

Так как f ’(c₁) > 0 и x - x ₀ < 0, то f(x) – f(x₀) < 0

 

2) Пусть x Î (x ₀; x ₀ +d). На отрезке [ x; x ₀] функция y = f (x) также удовлетворяет теореме Лагранжа. Значит на (x ₀; x) найдется хотя бы одна точка с₂, в которой выполняется равенство:

f (x) – f (x ₀) = f ’(c₂)×(x – x ₀), где c₂ Î (x ₀; x ₀+d).

Так как f ’(c₂) < 0 и x - x ₀ > 0, то f(x) – f(x₀) < 0

 

Следовательно, для любого x Î (x ₀-d; x ₀ +d) выполняется неравенство:

f (x ₀) > f (x).

Отсюда следует, что точка x ₀ является точкой максимума функции y = f (x).

Аналогично рассматривается случай, когда f ’(x) при переходе x через точку x ₀ изменяет знак с «+» на «-». При этом точка x ₀ является точкой минимума функции.

Теорема доказана.