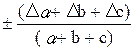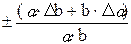Использование формул дифференцирования
Для определения абсолютных и относительных погрешностей искомой величины при косвенных измерениях можно воспользоваться формулами дифференцирования, потому что абсолютная ошибка функции равна абсолютной ошибке аргумента, умноженной на производную этой функции, то есть полному дифференциалу функции. Рассмотрим это более подробно. Допустим, что физическая величина А является функцией многих переменных: A = f (x, y, z...). Правило I. Вначале находят абсолютную погрешность величины А, а затем относительную погрешность. Для этого необходимо: 1) Найти полный дифференциал функции
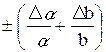
Применяя это правило к частным случаям, получим: - абсолютная погрешность суммы равна сумме абсолютных погрешностей слагаемых. Если X = a + b, то DX = Da + Db; - абсолютная погрешность разности равна сумме абсолютных погрешностей уменьшаемого и вычитаемого. Если X = a - b, то DX = Da + Db; - абсолютная погрешность произведения двух сомножителей равна сумме произведений среднего значения первого множителя (aCP) на абсолютную погрешность второго и среднего значения второго множителя (bCP) на абсолютную погрешность первого. Если X = а × b, то DX = aCP × Db + bCP × Dа. Если X = a n , то DX = n × аCPn-1 × Dа; - абсолютная погрешность дроби равна сумме произведения знаменателя на абсолютную погрешность числителя и числителя на абсолютную погрешность знаменателя, деленной на квадрат знаменателя. Если X = 3) По определению найдем относительную погрешность
Использование дифференциала натурального логарифма Во многих случаях, когда формула удобна для логарифмирования, оказывается более удобной другая последовательность действий: сначала находят относительную погрешность величины А, а затем абсолютную погрешность, поскольку относительная ошибка функции равна дифференциалу натурального логарифма этой функции. Действительно, относительная погрешность величины А есть ЕА = DA/Аср, но d(lnA) = DA/А и, следовательно, D(lnA) = DA/А. Правило II. 1) Логарифмируют функцию A = f (x, y, z,...). 2) Дифференцируют полученный логарифм по всем аргументам. 3) Заменяют бесконечно малые dx, dy, dz,... абсолютными ошибками соответствующих аргументов Dx, Dy, Dz, … (знаки "минус" в абсолютных ошибках аргументов заменяют знаками "плюс"). После вычислений получают относительную погрешность ЕА. 4) Абсолютную погрешность находят из формулы DA = ACP ×;EA.. Указания. 1. Если функция A = f (x, y, z,...) имеет вид, неудобный для логарифмирования, то для определения погрешностей пользуются правилом I. 2. Если функция A = f (x, y, z,...) имеет вид, удобный для логарифмирования, то для определения погрешностей пользуются правилом II. Рассмотрим следующие примеры: 1. В результате изучения равноускоренного движения некоторого тела получено выражение S = v0Чt + a Чt2/2, в котором v0 = (12 ± 1) м/с; a = (2.5 ± 0.4) м/с2; t = (30 ± 2) с; S = 12 × 30 + Для оценки абсолютной и относительной погрешностей при определении пути удобно пользоваться правилом I, так как функция неудобна для логарифмирования. Тогда
Так как DV0 = 1 м/с; Dt = 2 с; D a = 0.4 м/с2; V0 = I2 м/с; tСР = 30 с; a СР = 2,5 м/с2, то, подставив эти величины в формулу для DS, получим Полученный результат показывает, что при определении пути (1485) цифра 4 является сомнительной. Значит, S = 1500 м. Тогда ES = Окончательный результат будет иметь вид: S = (1500 2. При определении центростремительной силы, действующей на тело, вращающееся по окружности, пользуются формулой F = В результате измерений получено: m = (15.5 ± 0.2) кг; v = (3.45 ± 0.01) м/с; R= (150 ± 5) м; F = Для определения абсолютной и относительной ошибок при оценке центростремительной силы в данном случае удобно пользоваться правилом II, т.к. функция F = f (m,v,R) удобна для логарифмирования. Тогда ln F = ln m + 2 ln v - ln R. Продифференцировав это равенство, получим
Так как Dm = 0.2 кг; Dv = 0.01 м/с; DR = 5 м; mСР = 15.5 кг; vСР = 3.45 м/с; RСР = 150 м, то
DF = F × EF = 1.2299 Н ×0.052 = 0.06396 Н = 0.06 Н.
При определении центростремительной силы третья цифра слева является сомнительной и F =1.23 Н. Окончательный результат запишется в виде F = (1.23 ± 0.06) Н; EF = 5.2%. Используя первый или второй способы в расчете абсолютной и относительной ошибок измерений для часто встречающихся зависимостей, можно воспользоваться соответствующими формулами, которые сведены в таблицу 1. Таблица 1
|

 .
.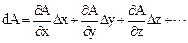 .
.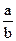 , то DX=
, то DX=  .
. .
. = 1485 м.
= 1485 м. .
. ×100% = 0.266 ×100% = 27%.
×100% = 0.266 ×100% = 27%. 400) м; ЕS = 27%.
400) м; ЕS = 27%. .
. = 1.2299 H.
= 1.2299 H. ;
;
 ; EF = 5.2%;
; EF = 5.2%;