Основные сведения из теории
Одной из особенностей нелинейных систем является возможность возникновения автоколебаний. Автоколебания – это собственные незатухающие периодические колебания, параметры которых определяются внутренними свойствами системы. Возможность возникновения автоколебаний в конкретной системе может зависеть в общем случае от вида и параметров нелинейностей, структуры линейной части и значений отдельных параметров динамических звеньев системы (коэффициентов передачи, постоянных времени), а также от начальных условий. Одним из наиболее широко распространенных методов исследования нелинейных систем является метод гармонической линеаризации. Он весьма удобен для определения условий возникновения автоколебаний и их параметров. В последнее время область его применения распространена на широкий класс задач исследований нелинейных систем (анализ вынужденных колебаний, определение показателей качества колебательных переходных процессов и др.). Для системы с одной нелинейностью и произвольной структурой линейной части основные положения метода гармонической линеаризации состоят в следующем. Пусть нелинейность выделена в отдельное звено со статической характеристикой y=F (x) и известна передаточная функция линейной части (рис.1):
Если на входе нелинейного звена действует гармонический сигнал x=a sin ω t, (2) выходной сигнал звена является периодической функцией сложной формы, которая может быть разложена в ряд Фурье:
Этот сигнал преобразуется линейной частью в соответствии с ее динамическими характеристиками. Если степень многочлена R (s) в числителе передаточной функции линейной части меньше степени многочлена Q (s) в знаменателе, то на высоких частотах значения амплитудно-частотной характеристики линейной части
Скорость уменьшения A л(ω) с увеличением частоты определяет наличие у линейной части свойства фильтра: A л(n ω)<< A л(ω), n= 2,3,… (4) При наличии такого свойства линейная часть (1) будет хорошо пропускать первую гармонику нелинейных колебаний (3) и ослаблять все высшие гармоники. Кроме того, в разложении Фурье, как правило, амплитуды гармоник с увеличением n также уменьшаются. Таким образом, ясно, что закон изменения сигнала x на входе нелинейного звена действительно окажется по форме близким к (2):
где наличие постоянной составляющей x 0 соответствует случаю несимметричных колебаний, обусловленных либо несимметричными нелинейностями, либо приложением внешнего воздействия. В этом случае задача расчета сводится к определению трех параметров: a*, ω*, x 0, а в случае симметричных колебаний – только a * и ω*. С учетом сказанного ясно, что для решения этой задачи в первом приближении достаточно исследовать прохождение по всей замкнутой цепи только первой гармоники сигнала y, то есть использовать следующее приближенное описание сигнала на выходе нелинейного звена:
Такое приближение в большинстве случаев обеспечивает удовлетворительную точность анализа процессов в нелинейных системах. Границы его применимости определяются наличием свойства фильтра у линейной части при ω=ω*. Соотношение (5) преобразуется следующим образом:
где F 0(x 0, a*) – постоянная составляющая сигнала на выходе нелинейного звена при несимметричных колебаниях, q (x 0, a*) и q' (x 0, a*) – коэффициенты гармонической линеаризации. Проведем раздельное исследование симметричных и несимметричных автоколебаний. А. Для случая симметричных колебаний (x 0=0, F 0(x 0, a*)=0) соотношения (6) упрощаются и вводится передаточная функция гармонически линеаризованного нелинейного звена:
Из (7) видно, что параметры и характеристики линеаризованного звена, в отличие от линейных звеньев, зависят не только от частоты, но и от амплитуды колебаний на входе. Выражения для коэффициентов гармонической линеаризации типовых нелинейностей приводятся в литературе [5,11]. Применение гармонической линеаризации нелинейной части САУ позволяет использовать для ее анализа результаты теории линейных систем. Из (1) и (7) получаем гармонически линеаризованное характеристическое уравнение замкнутой системы:
на основе которого определяется периодическое решение x*=a*sin ωt (симметричные автоколебания) из условия нахождения системы на колебательной границе устойчивости, получаемого по критерию Михайлова:
или
Если конечное решение уравнений (9) в области положительных вещественных чисел существует, соответствующие значения a* и ω* являются параметрами предельного цикла для данной нелинейной системы. Возможны несколько решений и соответственно несколько предельных циклов. Устойчивость предельного цикла может быть проверена по условию [5,11]
Если для найденной пары (a*,ω) условие (10) выполняется и все коэффициенты полинома, входящего в уравнение (8), положительны, в системе возможны автоколебания с частотой ω и амплитудой a* на входе нелинейного звена. В остальных случаях автоколебания в системе отсутствуют. Для системы выше четвертого порядка рассматриваются дополнительные условия [11]. Частотный способ определения автоколебаний основан на том, что в соответствии с критерием Найквиста колебательной границе устойчивости соответствует прохождение амплитудно-фазовой характеристики гармонически линеаризованной разомкнутой системы через точку (–1, j0). Следовательно, параметры возможных автоколебаний могут быть найдены решением уравнения
или
На комплексной плоскости строятся годограф W л(j ω) для Рассмотрим САУ, структурная схема которой представлена на рис. 3.
Передаточная функция линейной части системы имеет вид
Коэффициенты гармонической линеаризации нелинейности (рис. 4):
Из второго уравнения определим частоту периодического решения:
а из первого получаем
откуда можно определить амплитуду периодического решения. Проверку его устойчивости по критерию (10) предлагается провести самостоятельно. Отметим, что с учетом
При k л < k гр автоколебания в системе отсутствуют. Теперь рассмотрим нелинейную САУ, структурная схема которой показана на рис. 5. Для этой системы коэффициенты гармонической линеаризации имеют вид
Автоколебания будем определять частотным способом. Годограф данного нелинейного звена определяется функцией
Из рис. 6 в соответствии с частотным способом определения автоколебаний следует, что в рассматриваемой системе автоколебания невозможны при любых значениях параметров. Однако моделирование данной системы этот вывод не подтверждает. Отсюда заключаем, что в некоторых случаях применение метода гармонической линеаризации приводит к качественно неверным результатам.
Проверить наличие свойства фильтра у линейной части расчетным путем можно путем вычисления значений ее амплитудно-частотной характеристики для частот ω*, 2ω* 3ω*, найденных рассмотренным выше способом, или путем моделирования системы. Экспериментально наличие свойства фильтра может быть проверено путем подачи на вход линейной части разомкнутой системы гармонических сигналов с частотами ω*, 2ω*, 3ω* и измерения амплитуды выходного сигнала. Б. Перейдем к исследованию несимметричных колебаний, которые при симметричной нелинейности могут иметь место в статической системе при наличии постоянного внешнего воздействия. Пусть задана нелинейная САУ, динамика которой относительно входа
Если считать внешнее воздействие постоянным (
Как отмечалось выше, решение уравнения (14) ищется в форме
причем
Уравнение (15) разбивается на два следующих:
Параметры
или из эквивалентной системы нелинейных алгебраических уравнений:
Совместное решение системы уравнений (18) и уравнения (16) позволит найти искомые параметры автоколебаний
|


 . (1)
. (1) . (3)
. (3)
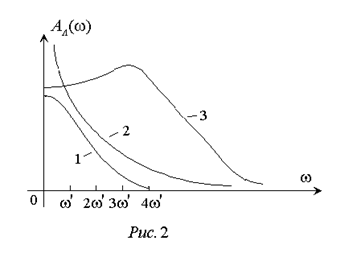 уменьшаются и при
уменьшаются и при  стремятся к нулю (рис.2).
стремятся к нулю (рис.2). или
или  ,
, . (5)
. (5)

 ,
, ,
, , (6)
, (6) ,
, . (7)
. (7) , (8)
, (8)
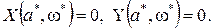 (9)
(9)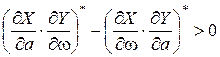 . (10)
. (10)
 . (11)
. (11) и годограф функции
и годограф функции  для
для 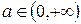 . Точки их пересечения дают параметры возможных автоколебаний, после чего применяются известные критерии устойчивости найденного периодического решения [5].
. Точки их пересечения дают параметры возможных автоколебаний, после чего применяются известные критерии устойчивости найденного периодического решения [5].
 .
.
 Уравнения (9) принимают вид
Уравнения (9) принимают вид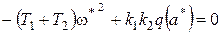 ,
, .
. ,
, , (12)
, (12) (рис. 4) уравнение (12) будет иметь решение только при
(рис. 4) уравнение (12) будет иметь решение только при .
.
 ,
,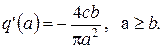
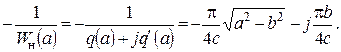
 Приведенный пример подтверждает, что метод гармонической линеаризации является приближенным в силу использования гипотезы о наличии у линейной части системы свойства фильтра. В частных случаях эта гипотеза может не подтвердиться даже при указанном выше соотношении степеней числителя и знаменателя передаточной функции линейной части. Поэтому после получения результатов на основе гармонической линеаризации целесообразна их расчетная или экспериментальная проверка.
Приведенный пример подтверждает, что метод гармонической линеаризации является приближенным в силу использования гипотезы о наличии у линейной части системы свойства фильтра. В частных случаях эта гипотеза может не подтвердиться даже при указанном выше соотношении степеней числителя и знаменателя передаточной функции линейной части. Поэтому после получения результатов на основе гармонической линеаризации целесообразна их расчетная или экспериментальная проверка. нелинейности описывается уравнением
нелинейности описывается уравнением . (13)
. (13)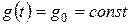 ), то для статических систем, у которых
), то для статических систем, у которых  , уравнение (13) упростится:
, уравнение (13) упростится: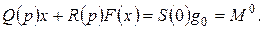 (14)
(14) ,
, являются искомыми параметрами автоколебаний. С учетом соотношений (6) уравнение (14) примет вид
являются искомыми параметрами автоколебаний. С учетом соотношений (6) уравнение (14) примет вид . (15)
. (15) (16)
(16) (17)
(17) гармонических колебаний находятся из характеристического уравнения, соответствующего уравнению (17):
гармонических колебаний находятся из характеристического уравнения, соответствующего уравнению (17):
 (18)
(18) при заданных параметрах системы.
при заданных параметрах системы.


