Основные сведения из теории. Частотный критерий В.М. Попова сформулирован для нелинейных систем с устойчивой линейной частью и позволяет исследовать устойчивость нулевого равновесного
Частотный критерий В.М. Попова сформулирован для нелинейных систем с устойчивой линейной частью и позволяет исследовать устойчивость нулевого равновесного состояния в целом, но не для одной фиксированной характеристики нелинейного элемента, а для некоторого семейства этих характеристик, принадлежащих к какому-либо классу [10,12. Определенное таким образом состояние равновесия называют абсолютно устойчивым. Наиболее часто для систем со структурной схемой, приведенной на рис.1, рассматривают нелинейные характеристики, заключенные в секторе [0,
При наличии одного нулевого полюса Пусть все полюсы
Кроме того, пусть нелинейная функция  определена следующим образом (рис. 2):
а вне этого отрезка лежит внутри заштрихованных секторов, то есть
причем выполнены условия:
Тогда, если найдется вещественное неотрицательное число
то при любых ограниченных начальных условиях процесс Частотное неравенство (3) совпадает с достаточным условием устойчивости, составляющим суть критерия В.М. Попова, и имеет ту же геометрическую интерпретацию с точностью до того, что допускается проведение прямой, проходящей через точку Как видно из приведенной формулировки, наклон прямой не должен быть отрицательным. Кроме того, условия (1) не допускают, чтобы Для того чтобы проверить выполнение критерия Гелига, следует построить годограф модифицированной частотной характеристики линейной части
где
и попытаться провести прямую, имеющую неотрицательный коэффициент наклона В лабораторной работе исследуется поведение следящей системы, в которой датчик рассогласования имеет зону нечувствительности, а усилитель –ограниченную зону линейности, то есть насыщение. Эти две нелинейности можно описать одной нелинейной зависимостью (рис.3). При
Из линейной теории следует, что пи соответствующем выборе параметров из условия
можно обеспечить заданные динамические свойства замкнутой линейной системы. Для нелинейной модели следящей системы достаточное условие устойчивости (3) можно записать в виде
или для случая ПФ линейной части (4) – в форме неравенства
где
Условию (5) можно дать специальную геометрическую интерпретацию. Если ввести условную частотную характеристику
|
]. Обратимся к структуре системы с нелинейностью, содержащей зону нечувствительности, и нейтрально устойчивой [5] линейной частью с передаточной функцией 
(рис. 1, 2).
положениями равновесия в системе являются любые точки внутри отрезка покоя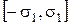 
. Для этого случая критерий В.М. Попова сохраняет силу при следующей модификации, предложенной А.Х. Гелигом [9,10].
.
(1)
(2)
такое, что 
не является полюсом 
выполнено частотное неравенство
(3)
остается огра-ниченным при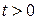 
, а при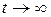 
и касающейся годографа модифицированной частотной характеристики [5,12].
,
проходящую через точку 
справа [5]. Если это удается, то отрезок покоя точечно устойчив в целом.
и 
приходим к линейной модели, если остальные элементы следящей системы описываются линейным соотношениями.
(4)
(5)
, 
– соответственно вещественная и мнимая части функции 
, причем
,
,
.
и построить ее годограф, то условие устойчивости (5) означает возможность провести прямую с неположительным коэффициентом наклона 
через точку 
так, чтобы годограф не заходил левее ее. По виду годографа 
можно определить предельное значение коэффициента передачи линейной части 
, превышение которого приводит к нарушению точечной устойчивости в целом рассматриваемого отрезка.
