Понятие лингвистической переменной и основные операции теории нечетких множеств.
Заде – ученый в 1979 разработавший ТНМ для отражения неопределенности предметной области. Лингвистической переменной называется кортеж элементов <N,T,M,C,S>, где N – наименование переменной T – множество значений или термов, представляющих собой наименование нечетких переменных, имеющих в качестве области определения множество из области принадлежности M. C – синтаксическая процедура, описывающая процесс образования из множества T новых осмысленных для данной задачи лингвистических переменных. S – семантическая процедура, позволяющая преписать новому элементу, образованному процедурой C некоторую семантику путем образования некоторого нечеткого множества. Обычно множество определяется характеристической функцией принадлежности элемента X множеству A.
Операции над нечеткими множествами Применимы все операции над множествами, но они претерпели некоторые изменения. 1. включение
2. равенство
3. пересечение множеств
4. объединение множеств Объединением называется наименьшее нечеткое множество, где мерой выбирается максимум
С помощью теории нечетких множеств вводятся нечеткие графы, где нечетко описываются вершины и дуги.
|
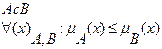
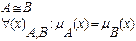
наибольшее нечеткое подмножество, содержащееся одновременно в А и в В
