Алгоритм обратного распространения ошибки
Данный алгоритм используется для полно связной сети. Суть алгоритма в распространении сигнала ошибки от входов сети последовательно через каждый скрытый слой на входе. Wij – связь, соединяющая i-ый нейрон предыдущего слоя с j-ым нейроном последующего слоя. Ошибка распространяется от выхода в сети к входам, т.е. направлении обратном функционированию сети в обычном режиме. Для минимизации ошибки используется функция отвеса yj,p - реальное состояние нейрона выходного слоя N при подаче на входы сети примера P d – желаемый выход нейрона для данного входного примера p. В процессе обучения выполняется минимизация ошибки E(W) методом градиентного спуска. Настройка весов осуществляется по правилу
Определяют общую производную функцию:
Для расчета величины
Для выходного слоя можно вычислить Теперь перепишем формулу (1) в раскрытом виде
Алгоритм состоит из следующих шагов: 1) на входы подается один из возможных примеров из множества P и рассчитываются потенциалы для всех слоев в режиме обычного функционирования сети
у каждого нейрона для получения выходного сигнала используется сигмоидальная функция активации. 2) по формуле (4) вычисляется - по формуле (3) вычисляется ошибка на предыдущем слое через последующий и по формуле (5) величина коррекции веса. Ошибки вычисляются для слов от N-1 до 1, т.е. n=N-1,…..,1 - корректируются все веса связей в нейронной сети - если общая ошибка E(W) больше заданной, то возвращаемся на шаг 1.
|
(0<i<1) (1)
вводится рекурсивная формула для расчета 
k – количество нейронов слоя (n+1)
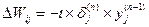
для выходного слоя.
