Загального положення
4. Частковим випадком плоско-паралельного переміщення є обертання фігури навколо осі, перпендикулярної до однієї з площин проекцій. При цьому усі точки фігури рухаються (переміщуються) по колах у площинах рівня, перпендикулярних до осі обертання. Центри кіл знаходяться у точках перетину осі із вказаними площинами. Якщо точка фігури знаходиться на осі обертання, то при обертанні системи ця точка вважається нерухомою. Таким чином, при обертанні навколо горизонтально-проецюючої осі, фронтальні проекції точок фігури переміщуються по прямих, перпендикулярних до ліній зв'язку, а горизонтальні – по дугах кіл. При обертанні навколо фронтально-проецюючої прямої горизонтальні проекції точок переміщуються по прямих, перпендикулярних до ліній зв'язку, а фронтальні – по дугах кіл. На рис. 5.5 показано обертання точки А навколо горизонтально-проецюючої прямої.
ί; – вісь обертання, пряма, навколо якої обертається точка, Вона обирається перпендикулярною до площин проекцій П1 або П2. S – площина обертання, тобто площину, в якій переміщується точка і яка перпендикулярна до осі обертання ί;. Якщо вісь обертання перпендикулярна до П1, то площина обертання буде горизонтальною; якщо до П2, то площина обертання буде фронтальною. т. О – центр обертання, точка перетину осі з площиною обертання
Приклад 1. Перетворити пряму загального положення в проецюючу пряму, визначити натуральну величину її відрізка АВ (рис. 5.6). При обертанні прямої навколо осі доводиться обертати дві її точки. Побудова спрощується, якщо вісь обертання провести через одну з кінцевих точок відрізка: вісь ί проводимо через точку А. ί ^ П2. Щоб визначити натуральну величину відрізка АВ, обертаємо його фронтальну проекцію до положення ІІ Х12. Таким чином відрізок АВ став горизонталлю, а горизонтальна проекція A1 ¢ B1 ¢ є його натуральною величиною. Для перетворення відрізка в проецююче положення здійснюємо обертання відрізка АВ навколо горизонтально-проецюючої осі q (q ^ П1), яку проводимо через точку В. Обертаємо горизонтальну проекцію до положення A1 ¢ B1 ¢ ^ Х12. Фронтальна проекція відрізка стане точкою: A2 º B2. Приклад 2. Визначити натуральну величину DАВС. DАВС – площина загального положення (рис. 5.7). Перетворення виконуємо послідовним подвійним обертанням. Спочатку перетворюємо площину загального положення в проецюючу площину. Для цього в площині DАВС проводимо одну із ліній рівня – h або f і обертаємо її до положення, коли вона стане перпендикулярною площині проекцій. При цьому лінія рівня спроецюється в точку, а площина – в лінію. Потім площину обертаємо навколо іншої проецюючої прямої до положення коли площина стане паралельною площині проекцій. На цю площину вона спроецюється в натуральну величину.
Рис. 5.7. 5. Обертання навколо горизонталі або фронталі застосовують, коли задану плоску фігуру потрібно сумістити з площиною рівня, паралельною площині проекцій. В такому положенні плоска фігура проецюється на відповідну площину проекцій в натуральну величину.
При обертанні навколо h точка А описує дугу кола у площині обертання S. Площина обертання S перпендикулярна до осі обертання: S ^ h. Таким чином, S є горизонтально-проецюючою площи-ною: S ^ П1. Центр обертання – точка О. О = S Ç h. Радіус обертання точки А (АО – відрізок прямої загального положення) знаходиться у площині S. Якщо радіус обертання точки А стане паралельним до П1, то він суміститься з площиною рівня, паралельною до П1, в якій знаходиться вісь обертання h. В цій самій площині рівня опиниться і точка А Î R. Таким чином, способом прямокутного трикутника визначаємо натуральну величину радіуса обертання точки А навколо h. Натуральну величину радіуса обертання відкладаємо від точки О1 на S1 (або за допомогою циркуля горизонтальну проекцію точки переміщуємо в нове положення А1), оскільки завжди R Ì S. В новому положенні точка А знаходиться з горизонталлю h в одній площині, яка паралельна П1. Друга проекція А¢2 в цьому випадку буде збігатися з проекцією h – h 2. Приклад 1: Визначити натуральну величину DАВС площини загального положення (рис. 5.9). Для визначення натуральної величини DАВС, через точки С і 1 проводимо горизонталь площини. Ці точки при обертанні будуть нерухомими, оскільки вони знаходяться на осі обертання h. Обертатись будуть лише точки А і В. Вони переміщуються по колах у площинах обертання, перпендикулярних до осі обертання h.
Радіус обертання точки А можна не знаходити, тому що точка А лежить на прямій 1-АВ, а положення двох точок цієї прямої ми визначили. В Î S; S ^ h; А Î L; L ^ h. Проекція А¢1В1С1 є натуральною величину DАВС, оскільки площина DАВС стала ІІ П1. Фронтальна проекція DАВС збігається з фронтальною проекцією h 2 горизонталі, тобто являє собою пряму лінію. 6. Спосіб допоміжного косокутнього проеціювання доцільно використовувати для розв’язання позиційних задач. Він полягає в тому, що напрям проеціювання вибирається таким чином, щоб пряма або площина, яка розглядається в задачі, займала проецююче положення.
Площину та пряму спроеційовано на поле П2 у напрямі горизонталі площини, при цьому площина спроеціюваласяя своїм фронтальним слідом, а пряма відрізком А¢2В¢2. Перетин цих двох прямих – точка D¢2, яку у зворотному напрямку проеціювання знаходимо на профільній прямій АВ. Приклад 2. Визначити лінію перетину двох площин загального положення заданих трикутними відсіками. Для визначення лінії перетину спроецюємо DАВС та DDFE на площину відповідності (бісекторну площину ІІ та ІV чверті простору). За напрямок проеціювання обираємо напрям сторона ВС, яка спроецюється в точку, а весь відсік DАВС – в лінію. Другий відсік DDFE спроецюється в трикутник DD4F4E4. В перетині отримаємо пряму M4N4, точки якої у зворотньому напрямі повертаємо на відповідні сторони DDFE. За допомогою конкуруючих точок 1, 2 та 3, 4 визначаємо видимість прямих на П1 та П2.
Рис. 5.11. Визначення лінії перетину двох площин способом допоміжного косокутного проеціювання Запитання для самоперевірки 1. Яке положення в системі 2. Як знайти довжину відрізка прямої лінії і кути цієї прямої з площинами П1 і П2, вводячи додаткові площини проекцій? 3. Скільки додаткових площин проекцій треба ввести в систему 4. Знайдіть способом плоско-паралельного переміщення натуральні величини відрізка прямої і трикутника, що лежать у фронтально-проецюючій площині. 5. Які основні елементи способу обертання? 6. У чому суть способу обертання навколо осей, перпендикулярних до площин проекцій? 7. Визначте способом обертання навколо проецюючих осей натуральні величини відрізка прямої і трикутника. 8. Як розміститься площина обертання точки, якщо її вісь обертання лише паралельна до площини П1 або до площини П2 але не перпендикулярна ні до П1 ні до П2? Чому при цьому доводиться визначати натуральну величину радіуса обертання? 9. Знайдіть способом суміщення натуральну величину трикутника, що лежить у горизонтально-проецюючій площині. 10. Що є ознакою досягнення горизонтального положення площини, заданої горизонталлю і точкою, при повороті навколо цієї горизонталі і де розміститься фронтальна проекція точки після повороту? ЛЕКЦІЯ 6.
|

 Рис.5.5. Обертання точки навколо горизонтально-проецюючої прямої
Рис.5.5. Обертання точки навколо горизонтально-проецюючої прямої
 Рис.5.6.
Рис.5.6.

 Рис.5.8.
Рис.5.8.
 Рис.5.9.
Рис.5.9.
 Рис.5.10.
Рис.5.10.

 займе площина П4, яка вводиться для утворення системи
займе площина П4, яка вводиться для утворення системи 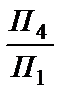 ?
?


