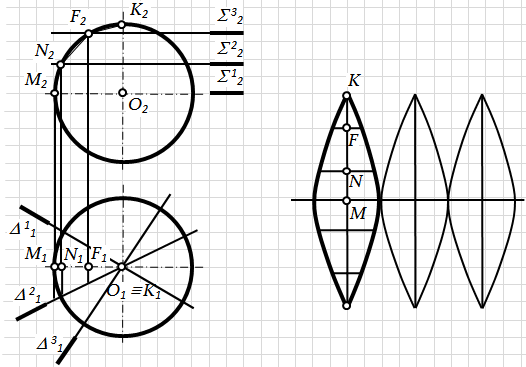РОЗГОРТКИ ПОВЕРХОНЬ.
План. 1. Переріз кривої поверхні площиною. 2. Види конічних перерізів. Переріз конуса площиною. 3. Перетин прямої лінії з поверхнею 4. Побудова лінії перетину поверхонь (загальний випадок). 5. Перетин многогранних поверхонь. 6. Перетин кривої поверхні з поверхнею многогранника. 7. Взаємний перетин кривих поверхонь. 8. Побудова лінії перетину поверхонь за допомогою січних сфер. 9. Розгортка поверхонь. Основні властивості розгортки. 10. Розгортка многогранних поверхонь. 11. Розгортка лінійчатих поверхонь.
1. При перерізах поверхонь площиною утворюється переріз, який обмежений плоскою кривою лінією, кожна точка якої є точкою перетину твірної з заданою січною площиною. Для побудови точок лінії перерізу застосовуються способи допоміжних січних площин або способи перетворення комплексного креслення. Допоміжні січні площини здебільшого вибираються площинами рівня або проецюючими, що дає можливість визначити множину точок перетину плоских ліній каркаса поверхні з заданою площиною. Способи перетворення проекцій дозволяють перевести площину в проецююче положення і цим спростити розв’язування задачі. При побудові лінії перетину необхідно в першу чергу визначити положення опорних (характерних) точок цієї лінії. До цих точок відносяться точки, які мінімально або максимально віддалені від площин проекцій, точки переходу видимої частини кривої в невидиму. Приклад 1. Побудувати проекції перерізу поверхні сфери проецюючою площиною S (рис. 7.1).
При перерізі поверхні сфери площи-ною утворюється коло. На горизонтальну пло-щину проекцій це коло спроецюється в еліпс. Характерні точки 1 і 2 визначаємо, як точки, що лежать на головному меридіані, а точки 3 і 3¢;, як точки, що лежать на екваторі сфери. Положення довільних точок 4 і 4¢;, 5 і 5¢; визначаємо за допомогою паралелей сфери, які проходять через ці точки.
Приклад 2. Побудувати проекції перерізу циліндра площиною загального положення S (h 0 ∩ f 0) (рис. 7.2). Внаслідок того, що бічна поверхня циліндра займає горизонтально-проецююче положення, горизонтальна проекція лінії перерізу відома – вона збігається з горизонтальним обрисом циліндра. А тому задача зводиться до визначення відсутньої фронтальної проекції лінії перерізу, виходячи з умови належності її точок січній площині S. Точки 1 і 2, в яких слід h 10 перетинає коло основи циліндра, будуть найнижчими точками кривої перерізу (еліпса).
Достатню кількість довільних точок лінії перерізу, а також точку 4, яка є межею видимості кривої у фронтальній проекції, визначаємо за допомогою фрон-тальних площин рівня. Ці площини перетинають задану січну площину по прямих лініях, а циліндр – по твірних. Точки перетину прямих з твірними, що належать відповідній фронтальній площині рівня, будуть шуканими точками лінії перерізу.
2. Залежно від положення січної площини в перерізі конуса можуть утворюватись (рис. 7.3): а) еліпс (повний або неповний), якщо січна площина перерізає всі прямолінійні твірні конічної поверхні; б) у частковому випадку – коли січна площина перпендикулярна до осі конічної поверхні – коло; в) парабола, якщо січна площина паралельна до однієї твірної конічної поверхні; г) гіпербола, якщо січна площина паралельна до двох твірних конічної поверхні; д) у частковому випадку – коли січна площина проходить через вершину конічної поверхні – гіпербола розпадається на дві пересічні прямі.
Рис.7.3. Види конічних перерізів
Приклад 1. Побудувати проекції перерізу поверхні прямого кругового конуса горизонтально-проецюючою площиною S (рис. 7.4). При перерізі конуса обертання горизонтально-проецюючою площиною S, яка паралельна до двох прямолінійних твірних конічної поверхні, в перерізі отримаємо гіперболу, горизонтальна проекція якої збігається зі слідом S1. Задача зводиться до побудови відсутньої фронтальної проекції цієї кривої. В перетині S1 з горизонтальною проекцією основи визначаються точки 11 і 21, а по них – проекції 12 і 22. Для визначення найвищої точки (вершини гіперболи) – 3 (31, 32), проведемо допоміжну горизонтально-проецюючу площину Δ; через вісь конуса перпендикулярно до сліду S1. Горизонтальну проекцію 31 шуканої точки 3 позначаємо в перетині S1 і Δ1. Визначивши фронтальну проекцію твірної SK, позначаємо на ній точку 32. Далі визначаємо точку 42, в якій фронтальна проекція гіперболи розділяється на видиму і невидиму частини. Ця точка знаходиться за допомогою твірної SN, яка є обрисною у фронтальній проекції. Для визначення інших точок гіперболи, можна провести декілька твірних в межах тієї частини поверхні конуса, яка позначена 154362, або декілька горизонтальних допоміжних січних площин. На рис. 7.4 за допомогою такої площини Φ; знайдені точки 6 і 7. Приклад 2. Побудувати проекції перерізу поверхні прямого кругового конуса площиною загального положення S (h 0 ∩ f 0) (рис. 7.5). Точки 1 і 2, в яких слід h 10 перетинає коло основи конуса, будуть найнижчими точками кривої перерізу (еліпса – січна площина перетинає всі прямолінійні твірні конічної поверхні).
Точку 4, в якій лінія перерізу у фронтальній проекції розділяється на дві частини – видиму і невидиму, визначаємо за допомогою допоміжної січної площини Δ;, яку проводимо через обрисні (контурні) твірні фронтальної проекції. Для визначення про-міжних точок лінії перерізу зручно скористатися горизон-тальними січними площинами, тому що вони перетинають поверхню конуса по колах, а 29 площину S – по горизонталях. Придатні для цих побудов лише ті площини, у яких фронтальні сліди знаходяться у межах між 1222 і 32, тому що у даному випадку вище точки 3 і нижче точок 1 і 2 не може бути точок, які належать лінії перерізу. На рис. 7.5 показано побудову точок 5 і 6 за допомогою площини Ф. Приклад 3. Побудувати проекції лінії перерізу поверхні конуса площиною загального положення S (f ∩ h) (рис. 7.6). Для спрощення розв'язання задачі здійснюємо заміну площини проекцій П2 на нову площину П4. Площину П4 вибираємо так, щоб по відношенню до неї січна площина S (f ∩ h) зайняла фронтально-проецююче положення. П4 ^ S. П4 ∩ П1 = Х14. Х14 ^ h 1. Спроецюємо на площину П4 конічну поверхню. Виконані перетворення дозволили звести розв'язання задачі до випадків, розглянутих вище (рис. 7.1 і 7.4), коли січна площина займає проецююче положення.
Рис.7.6. 3. Пряма перетинає поверхню другого порядку в двох точках, що називаються точками виходу і входу. Положення цих точок визначаємо за наступною схемою: 1. Через пряму проводимо допоміжну січну площину (найчастіше проецюючу). 2. Будуємо проекції перерізу поверхні січною площиною. 3. Оскільки переріз і пряма лежать в одній площині, то вони між собою перетинаються в двох точках, які є точками перетину прямої з поверхнею. Щоб отримати раціональне розв'язання цієї задачі, слід вибирати найбільш простий спосіб визначення лінії перерізу поверхні січною площиною. Цього можна досягти двома шляхами: 1) відповідним вибором положення січної площини; 2) переведенням прямої в особливе положення. Приклад 1. Побудувати проекції точок перетину поверхні сфери з прямою загального положення l (рис. 7.7).
2) Будуємо горизонтальну проекцію перерізу сфери площиною Σ; (див. рис. 7.1). 3) Визначаємо А1 і В1 – горизонтальні проекції точок зустрічі прямої зі сферою. Їх фронтальні проекції знаходимо за допомогою ліній зв'язку на фронтальній проекції l – l 2. Точка А знаходиться на верхній передній частині сфери, а тому є видимою на П1 і П2. Точка В знаходиться на нижній задній частині сфери і тому невидима на П1 і П2. Використання допоміжної проецюючої площини не завжди спрощує розв'язання, можливі випадки, коли в цій якості доцільно вибирати площину загального положення. Наприклад, при перетині конічної поверхні з прямою лінією такою є площина, яка проходить через вершину і тому перетинає цю поверхню по прямих лініях – твірних конічної поверхні. При перетині циліндричної поверхні з прямою лінією доцільно проводити допоміжну площину через задану пряму паралельно твірним цієї поверхні – така площина переріже циліндричну поверхню по прямих лініях – твірних циліндричної поверхні.
Точки перетину А і В будуємо за допомогою площини Σ;, яка визначається вершиною конуса і заданою прямою. Для визначення твірних, по яких площина Σ; перетинає конус, треба знайти ще по одній точці для кожної твірної, окрім точки S. Ці точки можуть бути знайдені в перетині горизонтального сліду площини Σ; – h S 0 – з колом основи конуса на П1. h S 0 знаходимо так: 1) будуємо горизон-тальний слід прямої l – точку 1; 2) у площині Σ про-водимо довільну пряму SK (точка К взята довільно на прямій l) і будуємо її горизонтальний слід – т. 2; 3) 1 Шукані твірні пройдуть через точки 3 і 4. Точки А і В є точками входу і виходу при перетині прямої l з поверхнею конуса.
4. При утворенні складних форм машинобудівних деталей чи інженерних конструкцій виникає потреба в побудові ліній перетину простих форм, що утворюють ці складні форми. Лінія, спільна для двох поверхонь, які перетинаються, називається лінією перетину. Для визначення проекцій лінії перетину необхідно знайти проекції точок, спільних для поверхонь, що розглядаються. Лінією перетину кривих поверхонь у загальному випадку є просторова замкнена крива лінія. Лінію перетину поверхонь, як і лінію перерізу поверхні площиною, будуємо за окремими точками. В першу чергу визначаємо характерні (опорні) точки. Це точки злому, екстремальні точки (крайні права і ліва, найближчі і найвіддаленіші, найвищі і найнижчі), точки розташовані на осях симетрії та інші, а також точки переходу видимої частини лінії перетину в невидиму (точки дотику проекції лінії перетину до контуру поверхні). Після цього визначаємо довільні точки лінії перетину. Кількість додаткових довільних точок і їх розташування визначається необхідною точністю побудови лінії перетину. Загальний метод побудови точок, які належать лінії перетину поверхонь, полягає в застосуванні поверхонь-посередників. За посередники слід вибирати поверхні, які перетинали б задані поверхні по найбільш простих для побудови лініях – прямих або колах. Тому найчастіше як поверхні-посередники використовують проецюючі площини, площини рівня, а також сфери. Важливо пам’ятати, що перш ніж вирішити питання, яку допоміжну січну поверхню-посередник вибрати для побудови лінії перетину поверхонь, слід з'ясувати, чи не займає одна з поверхонь, які перетинаються, проецююче положення, тому що в такому випадку розв'язання задачі значно спрощується, оскільки одна з проекцій лінії перетину буде збігатися зі слідом-проекцією проецюючої поверхні, яка входить в умову задачі. І тому розв'язання зводиться до визначення відсутньої проекції лінії, що належить поверхні, якщо відома одна її проекція і вказані проекції поверхні.
5. Лінія перетину двох многогранних поверхонь в загальному випадку являє собою замкнену просторову ламану лінію, побудову якої можна здійснювати двома способами, вибираючи серед них той, який дає найбільш простіші побудови: 1) Визначають точки, в яких ребра першої з поверхонь перетинають грані другої і ребра другої перетинають грані першої (задача на перетин прямої лінії з площиною). Через знайдені точки у певній послідовності проводять ламану лінію, яка являє собою лінію перетину заданих поверхонь. При цьому можна з'єднувати прямими проекції лише тих точок, які знаходяться в одній і тій самій грані. 2) Визначають відрізки прямих, по яких грані однієї поверхні, перетинають грані другої (задача на перетин двох площин між собою). Ці відрізки є частинами ламаної лінії, яка є лінією перетину многогранних поверхонь між собою. Якщо проекція ребра однієї з поверхонь не перетинає грані другої хоча б на одній з проекцій, то це ребро не перетинає цю грань. Водночас перетин проекцій ребра і грані ще не означає, що ці ребро і грань перетинаються у просторі. Приклад 1. Побудувати лінію перетину поверхонь: призми і піраміди (рис. 7.8).
Рис. 7.8. Перетин многогранних поверхонь
1. Проекції точок 1, 2, 3, 4 визначаємо з горизонтальної проекції (точки перетину ребер піраміди з гранями призми). 2. Проекції точок перетину ребра 2 призми з гранями піраміди визначаємо за допомогою допоміжної горизонтально проецюючої площини W (точки 5 і 6). 3. З’єднуємо точки між собою в такій послідовності: 1-3-5-4-2-6-1. Теоретичною основою цього питання є визначення точки перетину прямої з площиною. 6. Лінія перетину кривої поверхні з поверхнею многогранника складається з кількох частин, кожною з яких є плоска крива - лінія перетину кривої поверхні з гранню многогранника. Точки переходу однієї плоскої кривої в іншу (точки злому) є точками перетину ребер многогранника з кривою поверхнею. Таким чином, побудова лінії перетину кривої поверхні з поверхнею многогранника складається із задач: перетин прямої з поверхнею; побудова плоских перерізів. Приклад 1: Побудувати дві проекції лінії перетину прямого кругового конуса з наскрізним призматичним отвором (рис. 7.9).
Для цього на фронтальній проекції конуса (через відомі фронтальні проекції точок лінії перерізу) проводимо фронтальні проекції паралелей; знаходимо горизонтальні проекції цих паралелей; позначаємо точки (12≡1′2, 22≡2′2, 32≡3′2, 42≡4′2, 52≡5′2, 62≡6′2), в яких фронтальна проекція лінії перетину перетинає фронтальні проекції паралелей; знаходимо горизонтальні проекції точок 11, 1′1, 21, 2′1, 31, 3′1, 41, 4′1, 51, 5′1, 61, 6′1 на відповідних горизонтальних проекціях паралелей. З'єднавши їх плавними кривими, характер яких очевидний з умови задачі, отримаємо шукану горизонтальну проекцію лінії перерізу. 7. Приклад 1. Побудувати дві проекції лінії перетину напівсфери і прямого кругового конуса (рис. 7.10).
Для визначення положення точок 4, 4′, 5, 5′; використовуємо горизонтальні площини рівня. Наприклад, площина S З’єднавши отримані точки 2-5-4-1-4′-5′-3′; плавною кривою, одержуємо лінію перетину двох поверхонь Q і W. Важливо зазначити, що спільна площина симетрії не була паралельна П2, то необхідно було б виконати перетворення комплексного креслення так, щоб ця площина стала площиною рівня. 8. Для визначення лінії перетину двох довільних поверхонь обертання доцільно скористатися однією властивістю поверхонь обертання, яка полягає у тому, що дві будь-які співвісні поверхні обертання перетинаються по колах, які проходять через точки перетину меридіанів поверхонь. У частковому випадку, коли одна з поверхонь обертання – сфера, ця властивість може бути сформульована так: сфера з центром на осі поверхні обертання перетинає цю поверхню по колах, кількість яких дорівнює кількості точок перетину головних меридіанів поверхонь (рис. 7.11).
Поверхня сфери може перетинатися по колу не тільки з співвісною поверхнею обертання, але і з будь-якою іншою поверхнею, яка має кругові перерізи, наприклад, з конічною або циліндричною поверхнями другого порядку, що мають в основі коло, та ін. Побудувати лінії перетину поверхонь за допомогою допоміжних січних сфер можна двома способами: 1) способом концентричних сфер; 2) способом ексцентричних сфер. Особливості кожного з цих способів і умови їх застосування прослідкуємо на конкретних прикладах. Для двох поверхонь обертання, осі яких перетинаються, точка перетину осей може бути взята за центр концентричних сфер. Спосіб концентричних сфер застосовується при побудові лінії перетину поверхонь, осі яких паралельні до однієї з площин проекцій і перетинаються. Приклад 1. Побудувати лінію перетину циліндра обертання з фронтальною віссю і конуса обертання з фронтальною віссю. Осі поверхонь перетинаються в точці О (рис. 7.12).
Рис.7.12.
Спільна площина симетрії, яка проходить через осі поверхонь і паралельна до фронтальної площини проекцій, дає можливість визначити опорні (крайні) точки А і В, які знаходяться безпосередньо на перетині обрисних твірних конуса і циліндра на П2. Для визначення точок С2, С ¢ 2, D2, D ¢ 2 з центру О2 проведемо дві довільні сферичні поверхні. Сфери перетинаються з поверхнями по колах. Точки перетину двох кіл, що належать одній сфері, дають дві шукані точки С2 і С ¢ 2, які на фронтальній проекції збігаються в одну. Радіуси січних сфер вибирають довільно в межах від Rmin до Rmax. Rmax дорівнює відстані від фронтальної проекції точки О до найвіддаленішої проекції крайньої точки. Для визначення Rmin необхідно виявити, яка сфера найменшого радіусу перетинає одну з поверхонь і дотикається до іншої – як правило, це сфера, вписана в одну з поверхонь, які перетинаються. У даному прикладі мінімальний радіус сфери дорівнює радіусу сфери вписаної в конус, а максимальний – сфера, що проходить через крайню т. А. Спосіб ексцентричних сфер може бути використаний для побудови лінії перетину двох поверхонь, які мають спільну площину симетрії. При цьому кожна поверхня повинна мати кругові перерізи. Як і у способі концентричних сфер, площина симетрії повинна бути паралельною одній із площин проекцій, але центри січних сфер не збігаються в одній точці, а знаходяться на спільній прямій – осі однієї з поверхонь, що перетинаються. Приклад 2. Побудувати фронтальну проекцію лінії перетину конуса з частиною тора (рис. 7.13).
Рис.7.13.
Найвища та найнижча точки (А і В) – визначаються безпосередньо на перетині контурної твірної тора з контурними твірними конуса. Переріжемо поверхню кільця фронтально-проецюючою площиною Δ;, що проходить через вісь тора. Ця площина переріже поверхню тора по колу, фронтальна проекція якого – відрізок 1222. Це ж саме коло може бути отримане, якщо поверхню кільця перерізати ексцентричними сферами, центри яких розміщені на перпендикулярі, проведеному через центр кола 1-2 до площини Δ;. Для того, щоб допоміжна сфера перерізала по колу і поверхню конуса обертання, необхідно щоб її центр належав осі конуса. Тому за центр допоміжної сфери слід взяти точку перетину перпендикуляра з віссю конуса. У цьому випадку сфера, радіус якої дорівнює відстані від її центра до точки 1 (або 2) переріже обидві поверхні по колах. Коло 3-4, по якому ця сфера перетинає конус, є паралеллю конуса. Кола 1-2 і 3-4 перетинаються в точках D, D ¢ (D2, D ¢ 2), які є спільними для двох заданих поверхонь. Аналогічно, за допомогою серії фронтально-проецюючих площин (S і т.п.), що перетинають поверхню тора по колах і проводяться між крайніми точками А і В, будуємо достатню кількість довільних точок шуканої лінії перетину: С, С ¢ (С2, С ¢ 2) і т.п При взаємному перетині двох кривих поверхонь другого порядку можливі випадки, коли просторова крива четвертого порядку взаємного перетину двох поверхонь розпадається на дві плоскі криві другого. Теорема Монжа. Якщодві поверхні другого порядку описані навколо третьої поверхні другого порядку або вписані в неї, то лінія їх перетину розпадається на дві криві другого порядку, площини яких проходять через пряму, яка з'єднує точки перетину ліній дотику. Практичне використання теореми можливе у тому випадку, коли дві поверхні обертання другого порядку можуть бути описані навколо сфери або вписані в неї (рис. 7.14).
Рис.7.14. Рис. 7.15 дає уяву про те, як можна визначити лінії перетину двох конічних поверхонь D і Q, описаних навколо сфери W. Поверхня D дотикається до сфери W по колу, фронтальна проекція якого 1222, а поверхня Q – по колу, яке проецюється в 3242. Точки перетину цих кіл А і В є точками дотику поверхонь D і Q. Відповідно теоремі Монжа площини кривих l 1 і l 2 повинні проходити через пряму АВ. Оскільки АВ ^ П2, то площини T É l 1 і R É l 2 – фронтально-проецюючі, а криві l 1 і l 2 проецюються у відрізки С2D2 і E2F2. Наведені на рис. 7.15 конічні поверхні D і Q перетинаються по двох кривих, одна з яких l 1 – еліпс, а друга l 2 – парабола (див. рис. 7.3).
Рис. 7.15. 9. Розгорткою поверхні називається плоска фігура, що утворюється при суміщенні поверхні з площиною. Поверхні, які не можуть бути суміщені з площиною, відносяться до нерозгортних поверхонь. До групи розгортних поверхонь відносяться тільки лінійчаті поверхні і, зокрема ті з них, які мають пересічні суміжні твірні. Точка перетину може бути як власною (поверхні з ребром звороту і конічні), так і невласною (циліндричні поверхні). Деякі геометричні властивості елементів поверхонь не змінюються при розгортці. Оскільки розгортка поверхні являє собою плоску фігуру, утворену з поверхні без розривів і склеювання, то кожній точці (фігурі) на поверхні відповідає точка (фігура) на розгортці і навпаки. Звідси випливають основні властивості розгортки поверхонь: 1. Довжини двох відповідних ліній поверхні та її розгортки рівні між собою, наслідком чого є те, що замкнена лінія на поверхні і відповідна їй лінія на розгортці обмежують однакову площу. 2. Кут між лініями на поверхні дорівнює куту між відповідними їм лініями на розгортці. 3. Прямій на поверхні відповідає також пряма на розгортці (зворотне твердження не має змісту). 4. Паралельним прямим на поверхні відповідають також паралельні прямі на розгортці. В залежності від виду поверхонь їхні розгортки можуть бути: точними, наближеними і умовними. Точна розгортка може бути побудована лише для многогранників та відсіків розгортних поверхонь (циліндра, конуса, торса) – поверхню многогранника завжди можна сумістити з площиною, тому що вона складається з плоских відсіків. Побудова точної розгортки похилого конуса або циліндра пов’язана з обчисленням довжини кривої лінії, що само по собі ставить не просту задачу. Тому розгортку будують наближено, замінюючи поверхню конуса многогранною пірамідою, а поверхню циліндра поверхнею многогранної призми. При побудові розгортки нерозгортних поверхонь (сфера, тор) їх апроксимують відсіками розгортних поверхонь і будують розгортки цих відсіків. Сукупність розгорток відсіків розгортних поверхонь, якими замінюється нерозгортна поверхня, називається умовною наближеною розгорткою нерозгортної поверхні. Побудова розгорток має велике практичне значення, тому що дозволяє виготовляти різноманітні вироби з плоского (листового) матеріалу шляхом його згинання. 10. Розгорткою многогранної поверхні є плоска фігура, яка складається з граней цієї поверхні, суміщених з одною площиною. Для того, щоб при побудові розгортки многогранника його грані зобразились неспотворено, вони суміщаються з площиною, паралельною площині проекцій. Існує три способи побудови розгортки многогранних поверхонь: 1) спосіб трикутників (тріангуляції); 2) спосіб нормального перерізу; 3) спосіб розкочування. Розглянемо на прикладах кожен з наведених способів. Приклад 1. Побудувати розгортку бічної поверхні піраміди SАВС (рис. 7.16).
Рис. 7.16. Розгортка поверхні методом тріангуляції
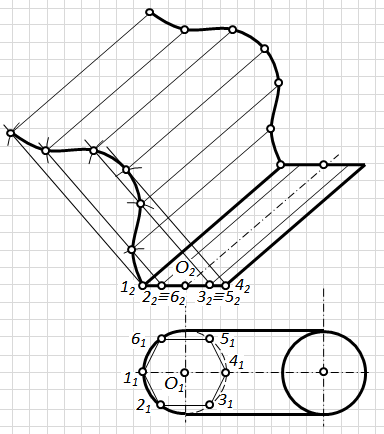
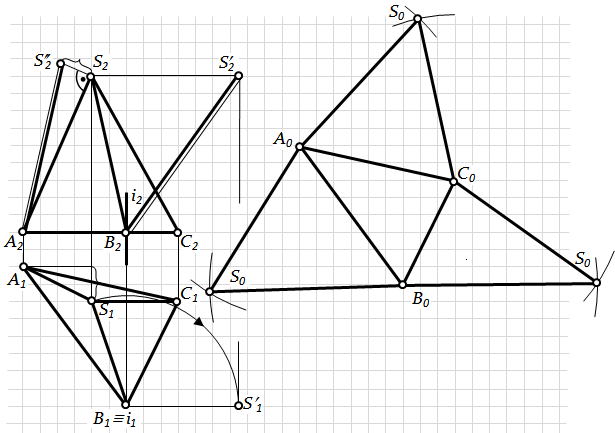
Розгортка бічної поверхні піраміди являє собою плоску фігуру, яка складається з трикутників – граней піраміди, і проводиться за наступною схемою: 1) визначається натуральна величина ребер і сторін основи піраміди; 2) в площині креслення послідовно способом засічок будуються натуральні величини трикутників (граней). На рис. 7.16 довжина ребра піраміди SА визначена способом прямокутного трикутника, ребра SВ – обертанням навколо проецюючої прямої ί; É S, ребро SС паралельне фронтальній площині проекцій, а тому проецюється на П2 в натуральну величину. Після того, як визначені довжини ребер ½ S¢¢2А2 ½,½ S¢2В2 ½,½ S2С2 ½ переходимо до побудови розгортки. Для цього на вільному полі креслення будуємо трикутник основи А0В0С0, яка на П1 спроеціювалася в натуральну величину. З точки А0 проводимо дуги радіусом АS, з точки В0 – дуги радіусом ВS, з точки С0 – дуги радіусом СS. Точки перетину дуг визначать положення точок S0 і, відповідно, ребер А0S0, В0S0, С0S0 на розгортці. Приклад 2. Побудувати розгортку похилої тригранної призми АВСDEF (рис. 7.17).
Рис. 7.16. Розгортка поверхні способом нормального перерізу
1) Перерізаємо призму площиною S, яка перпендикулярна до бічних ребер. Будуємо переріз заданої призми цією площиною (D123). 2) Визначаємо довжини сторін D123 (відрізків ламаної лінії, яка отримана при перерізі поверхні призми цією площиною) обертанням навколо фронтально-проецюючої прямої ί; É 3. 3) Ламану розгортаємо в пряму. Для цього на вільному полі креслення проведемо довільну горизонтальну пряму а. Від довільної точки 10, взятої на цій прямій, відкладаємо відрізки ½ 1020 ½,½ 2030 ½,½ 30 1 0 ½, довжини яких дорівнюють довжинам сторін трикутника D123. Через точки 10 , 20 , 30 , 10 проведемо прямі, перпендикулярні до прямої а, і відкладемо на них від точок 10 , 20 , 30 , 10 відрізки, довжини яких дорівнюють відповідним довжинам бічних ребер (½ 1A ½,½ 1D ½,½ 2B ½,½ 2E ½, …….). Отримані точки А0В0С0 та D0E0F0 з'єднуємо прямими. Плоска фігура А0В0С0А0D0E0F0D0 являє собою розгортку бічної поверхні призми. На рис.7.17 ребра АD, ВE і СF паралельні площині П2, тому вони проецюються на цю площину без спотворення. Якщо ребра призми займають довільне положення, то перш ніж перейти до побудови розгортки, слід за допомогою способів перетворення комплексного креслення перевести їх у положення, паралельне до якоїсь площини проекцій. Щоб отримати повну розгортку призми, необхідно до розгортки бічної поверхні добудувати основи призми – DА0В0С0 та DD0E0F0, побудова яких очевидна з рис. 7.16. В тому випадку, якщо основи призми займають загальне положення, слід попередньо визначити їх неспотворені розміри. Спосіб розкочування доцільно використовувати для побудови розгортки поверхні призми у тому випадку, коли основа призми паралельна до якоїсь одної площини проекцій, а її ребра паралельні іншій площині проекцій. Приклад 3. Побудувати розгорткупохилої тригранної призми АВСDEF (рис. 7.17). Приймемо за площину розгортки площину D, яка проходить через ребро АD і паралельна до фронтальної площини проекцій. Сумістимо грань ADEB з площиною D. Для цього уявно розріжемо бічну поверхню призми по ребру АD, а потім повернемо грань ADEB навколо ребра АD (А2D2). Для визначення суміщеного з площиною D положення ребра В0Е0 з точки В2 проводимо промінь, перпендикулярний до А2D2, і засікаємо на ньому дугою радіуса | А1В1 |, проведеною з центру А2, точку В0. Через В0 проводимо пряму В0Е0, паралельну А2D2. Приймаємо суміщене положення ребра В0Е0 за нову вісь обертання і повертаємо навколо неї грань ВЕFС до суміщення з площиною D. Для цього з точки С2 проводимо промінь, перпендикулярний до суміщеного ребра В0Е0, а за точки В0 – дугу кола радіусом, рівним | В1С1 |; перетин дуги з променем визначить положення точки С0. Через С0 проводимо С0F0 паралельно В0Е0. Аналогічно знаходимо положення ребра А0D0. З'єднавши точки А2В0С0А0 і D2E0F0D0 прямими, отримаємо фігуру А2В0С0А0D0F0E0D2 – розгортку бічної поверхні призми. Для отримання повної розгортки призми досить до якої-небудь з частин ламаної лінії А2В0С0А0 і D2E0F0D0 добудувати трикутники основи A0B0C0 та D0E0F0.
Рис. 7.17. Розгортка поверхні способом розкочування
11. Вище ми визначали, що до розгортних поверхонь відносяться тільки поверхні з ребром звороту, конічна та циліндрична. Розгортка будь-якої розгортної поверхні (окрім гранних) є наближеною. Це пояснюється тим, що при розгортці поверхні її апроксимують поверхнями вписаних або описаних многогранників, які мають грані у вигляді прямокутників або трикутників. Тому при графічному виконанні розгортки поверхні завжди доводиться здійснювати розгинання чи спрямлення кривих ліній поверхні, що неминуче призводить до втрати точності. Розглянемо способи побудови розгорток двох поверхонь, що широко використовуються в практиці: конічної і циліндричної. Розгортка бічної поверхні прямого кругового конуса являє собою круговий сектор, радіус якого дорівнює довжині твірної конічної поверхні L = SA, а центральний кут j =
Рис. 7.18. Розгортка бічної поверхні прямого кругового конуса
Задача на побудову розгортки бічної поверхні похилого конуса розв'язується так само, як і у випадку побудови розгортки бічної поверхні піраміди – способом трикутників: 1) Коло основи замінюється многокутником (на рис. 7.19 – восьмикутник), а конічна поверхня замінюється поверхнею піраміди з трикутними гранями. 2) Визначається натуральна величина ребер піраміди (на рис. 7.19 це зроблено способом обертання навколо проецюючої прямої); 3) Будується розгортка бічної поверхні піраміди (рис. 7.20). Фігуру S010203040……10 приймаємо за наближену розгортку конічної поверхні. Чим більша кількість граней у вписаної піраміди, тим меншою буде різниця між дійсною і наближеною розгортками конічної поверхні.
Рис. 7.19. Побудова розгортки бічної поверхні похилого конуса
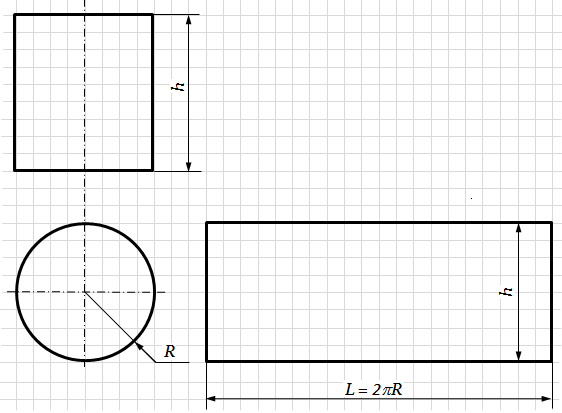
Рис. 7.20. Розгортка бічної поверхні похилого конуса Розгорткою бічної поверхні прямого циліндра є прямокутник, довжина якого дорівнює довжині кола основи циліндра, тобто L = 2pR, а висота – дорівнює висоті циліндра h (рис. 7.21).
Рис. 7.21. Розгортка циліндричної поверхні
Для побудови розгортки бічної поверхні похилого циліндра використовуються ті ж самі способи нормального перерізу і розкочування, якими користувалися при розгортці бічної поверхні призми. В обох випадках циліндричну поверхню замінюють призматичною поверхнею, вписаною (або описаною) в задану циліндричну. Потім задачу розв’язують так, як це було показано у прикладах на рис. 7.16 і 7.17. На рис. 7.22 показано побудову розгортки бічної поверхні еліптичного циліндра способом розкочування. Необхідні геометричні побудови виконуємо у наступній послідовності: 1. Ділимо коло основи циліндра на n рівних частин (на рис. 7.22 n = 6, точність побудов зростає зі збільшенням n). 2. Через точки поділу проводимо прямолінійні твірні циліндричної поверхні - ребра призми, якою ми замінюємо циліндричну поверхню D. 3. Приймаємо за площину розгортки фронтальну площину S, яка проходить через ребро 1 призми, тотожне 1 -й твірній циліндричної поверхні. Подальші побудови аналогічні виконаним на рис.7.17 при побудові розгортки бічної поверхні призми ABCDEF. Таким чином, розгорткою бічної поверхні похилого циліндра є плоска фігура, обмежена з двох боків прямими твірними, а з двох інших боків кривими – розгортками кривих основ циліндра (рис. 7.22). Якщо твірні циліндра є прямими загального положення, то необхідно перетворенням комплексного креслення зробити так, щоб твірні циліндра зобразились в натуральну величину.
Рис. 7.22. Розгортка еліптичного циліндра 12. Теоретично нерозгортна поверхня не має своєї розгортки. Але на практиці для отримання необхідної нерозгортрої поверхні з листового матеріалу будують так звані умовні (наближені) розгортки нерозгортних поверхонь. При цьому доводиться окрім згинання здійснювати також стискування і розтягування певних ділянок листа. Загальний метод розв’язання задачі на побудову умовної розгортки нерозгортної поверхні полягає у тому, що відсіки заданої поверхні замінюються відсіками розгортної поверхні з наступною побудовою розгортки цієї поверхні. Переріжемо поверхню сфери горизонтально-проецюючими площинами D1, D2, D3, …, які проходять через центр сфери, на кілька рівних ділянок (скибок). Після цього одна з ділянок горизонтальними площинами рівня S1, S2, S3, … розрізається на плоскі многокутники (трикутник і трапеції) (рис. 7.23). Елементи многокутників будуть проеціюватися в натуральну величину на П1 або П2. По цих елементах будуємо дійсну величину однієї ділянки (рис. 7.23). Повна розгортка поверхні сфери буде складатися з розгорток усіх ділянок (скибок).
Рис. 7.23. Розгортка поверхні сфери Запитання для самоперевірки 1. Як будується крива лінія при перетині кривої поверхні площиною? 2. По яких лініях перетинається циліндрична поверхня площиною, проведеною паралельно до твірної цієї поверхні? 3. Які лінії отримують при перетині циліндра обертання площинами? 4. Як треба провести площину, щоб конічна поверхня перетиналась по прямих лініях? 5. Які криві отримують при перетині конуса обертання площинами? 6. Яку криву отримують при перетині сфери будь-якою площиною і якими можуть бути проекції цієї лінії? 7. У чому полягає загальний метод побудови точок перетину прямої лінії з кривою поверхнею? 8. Як провести допоміжну січну площину при перетині конуса прямою лінією, щоб отримати на поверхні конуса прямі лінії? 9. У чому полягає загальний метод побудови лінії перетину однієї поверхні іншою? 10. Які точки лінії перетину поверхонь називаються "характерними?" 11. Як будується лінія перетину однієї многогранної поверхні іншою? 12. У яких випадках для побудови лінії перетину однієї поверхні іншою рекомендується використовувати допоміжні січні площини, паралельні площинам проекцій? 13. По яких лініях перетинаються між собою: а) циліндричні поверхні, твірні яких паралельні між собою, б) конічні поверхні зі спільною вершиною? 14. Як можна використати випадок, коли одна з поверхонь, які перетинаються, займає проецююче положення? 15. У яких випадках для визначення лінії перетину двох поверхонь можна використати спосіб концентричних сфер? ексцентричних сфер? 16. Які лінії одержують при взаємному перетині двох поверхонь обертання, описаних навколо спільної для них сфери або вписаних у сферу? 17. По яких лініях перетинаються між собою дві співвісні поверхні обертання? 18. Вкажіть способи, які використовуються для побудови проекцій лінії перетину поверхонь? 19. Що називається розгорткою поверхні? 20. Які поверхні відносяться до розгортних? 21. Назвіть властивості поверхні, які зберігаються на її розгортці? 22. Назвіть способи побудови розгорток і сформулюйте зміст кожного з них. 23. В яких випадках для побудови розгортки використовуються способи: нормального перерізу, розкочування, трикутників? 24. У чому полягає загальний прийом розв’язання задачі на побудову умовної розгортки нерозгортних поверхонь? 25. Як можна побудувати розгортку зрізаної конічної поверхні з недосяжною вершиною? 26. Який спосіб доцільно використати для побудови умовної розгортки поверхні сфери?
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Бубеников А.В. Начертательная геометрия / А.В. Бубеников 2. Крылов Н.Н. Начертательная геометрия / Н.Н. Крылов, Г.С. Икон-никова, В.Л. Николаев, В.Е. Васильев; под ред. Н.Н. Крылова – М.: Высшая школа, 2002. – 224 с. 3. Михайленко В.Є. Нарисна геометрія / В.Є. Михайленко, М.Ф. Євстіфеєв, С.М. Ковальов, О.В. Кащенко: під ред. В.Є. Михай-ленка. – К.: Вища школа, 2004. – 303 с. 4.
ЗМІСТ
|

 Рис.7.1
Рис.7.1
 Рис.7.2
Рис.7.2

 Рис.7.4
Рис.7.4
 Рис.7.5
Рис.7.5

 Рис.7.7
Рис.7.7
 Рис.7.7
Рис.7.7
 2 = h S0.
2 = h S0.
 Рис.7.9
Рис.7.9
 Рис.7.10
Рис.7.10
 перерізає поверхню напівсфери по колу радіуса R (проекції a1, a2), а поверхню конуса по колу радіуса r (проекції b2, b1), ці два кола перетинаються між собою в точках 4 і 4′;. Спочатку визначаємо горизонтальні проекції цих точок – 4′1 і 41, а потім по лініях зв’язку визначаємо положення фронтальних проекцій цих точок – 42 і 4′2, знаючи, що вони лежать на фронтальних проекціях ліній a2 і b2.
перерізає поверхню напівсфери по колу радіуса R (проекції a1, a2), а поверхню конуса по колу радіуса r (проекції b2, b1), ці два кола перетинаються між собою в точках 4 і 4′;. Спочатку визначаємо горизонтальні проекції цих точок – 4′1 і 41, а потім по лініях зв’язку визначаємо положення фронтальних проекцій цих точок – 42 і 4′2, знаючи, що вони лежать на фронтальних проекціях ліній a2 і b2. Рис.7.11
Рис.7.11






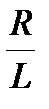 ´ 360
´ 360  , де R – радіус кола основи конуса. (рис. 7.18).
, де R – радіус кола основи конуса. (рис. 7.18).