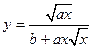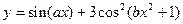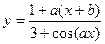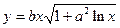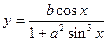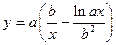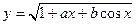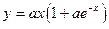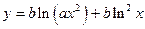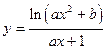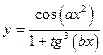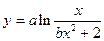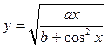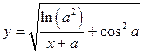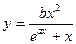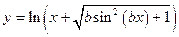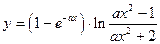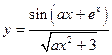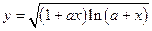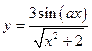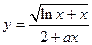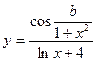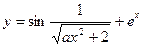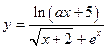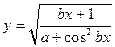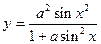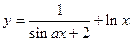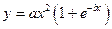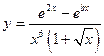Лабораторная работа № 3. Тема: Операторы повторений
Тема: Операторы повторений
Задание.
Составить схему алгоритма и программу а языке Паскаль для вычисления значений функции y=f(x) в точках от 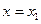 до до 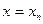 c шагом c шагом 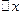 . При выполнении задания использовать операторы цикла с постусловием, с предусловием и оператор цикла с параметром. . При выполнении задания использовать операторы цикла с постусловием, с предусловием и оператор цикла с параметром.
Результаты вычислений оформить в виде таблицы, используя символы псевдографики. Коды символов приведены в таблице. Для вставки нужного символа в текст программы держите нажатой клавишу ALT при наборе кода. Код набирать на ЦИФРОВОЙ КЛАВИАТУРЕ. Коды символов приведены в таблице 3.1.
Таблица 3.1
| Одинарная рамка
| Двойная рамка
| Горизонтальные элементы
| Вертикальные элементы
| | ┌ ┬ ┐
218 194 191
├ ┼ ┤
195 197 180
└ ┴ ┘
192 193 217
| ╔ ╦ ╗
201 203 187
╠ ╬ ╣
204 206 185
╚ ╩ ╝
200 202 188
| ─ 196
═ 205
| │ 179
║ 186
|
Варианты заданий к лабораторной работе № 3
Таблица 3.2
| Номер варианта
| y = f(x)
| Исходные данные
| |
| 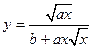
| x 1 = 1; x n = 2;
Δ x = 0,2;
a = 3,5;
b = 1,2
| |
| 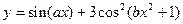
| x 1 = 0; x n = 5;
Δ x = 0,5;
a = 0,5;
b = 0,7
| |
| 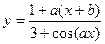
| x 1 = 1; x n = 3;
Δ x = 0,2;
a = 3,9;
b = 2,3
| |
| 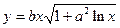
| x 1 = 2; x n = 3;
Δ x = 0,1;
a = 4;
b = 7
| |
| 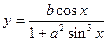
| x 1 = 1; x n = 6;
Δ x = 0,5;
a = 0,57;
b = 9
| |
| 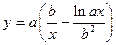
| x 1 = 2; x n = 5;
Δ x = 0,5;
a = 1,5;
b = 4,8
| |
| 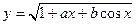
| x 1 = 2; x n = 8;
Δ x = 0,7;
a = 4,2;
b = 1,5
| |
| 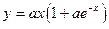
| x 1 =2; x n = 7;
Δ x = 0,5;
a = 3,5;
| |
| 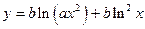
| x 1 = 1; x n = 4;
Δ x = 0,3;
a =4,3;
b = 5,4
| |
| 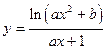
| x 1 = 2; x n = 4;
Δ x = 0,4;
a = 1,4;
b = 2,5
| |
| 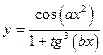
| x 1 = 0; x n = 1;
Δ x = 0,1;
a = 2,1;
b = 0,3
| |
| 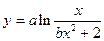
| x 1 = 3; x n = 6;
Δ x = 0,3;
a = 1,9;
b = 1,1
| |
| 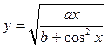
| x 1 = 3; x n = 5;
Δ x = 0,2;
a = 1,9;
b = 1,1
| |
| 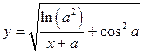
| x 1 = 5; x n = 8;
Δ x = 0,2;
a = 5,3;
| |
| 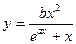
| x 1 = 2; x n = 8;
Δ x = 0,6;
a = 1,9;
b = 1,1
| |
| 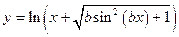
| x 1 = 1; x n = 5;
Δ x = 0,4;
b = 5,7
| |
| 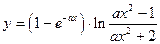
| x 1 = 4; x n = 7;
Δ x = 0,3;
a = 3,8
| |
| 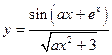
| x 1 = 3; x n = 9;
Δ x = 0,6;
a = 2,7
| |
| 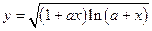
| x 1 = 1; x n = 5;
Δ x = 0,4;
a = 5,3
| |
| 
| x 1 = 2; x n = 4;
Δ x = 0,1;
a = 4,5
| |
| 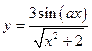
| x 1 = 3; x n = 5;
Δ x = 0,1;
a = 4,5
| |
| 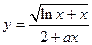
| x 1 = 1; x n = 3;
Δ x = 0,2; a = 2,8
| |
| 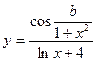
| x 1 = 3; x n = 9;
Δ x = 0,3;
b = 0,71
| |
| 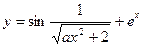
| x 1 = 0; x n = 3;
Δ x = 0,2;
a = 3,9
| |
| 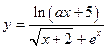
| x 1 = 5; x n = 9;
Δ x = 0,4;
a = 2,4
| |
| 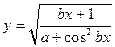
| x 1 = 1; x n = 3;
Δ x = 0,2;
a = 4,1;
b = 4,7
| |
| 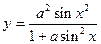
| x 1 = 0; x n = 2;
Δ x = 0,2;
a = 1,92
| |
| 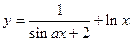
| x 1 = 1; x n = 4;
Δ x = 0,3;
a = 1,8
| |
| 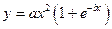
| x 1 = 1; x n = 3;
Δ x = 0,2;
a = 0,8;
b = 4,2
| |
| 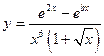
| x 1 = 1; x n = 5;
Δ x = 0,4;
b = 0,37
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Методы анализа финансово-хозяйственной деятельности предприятия
Содержанием анализа финансово-хозяйственной деятельности предприятия является глубокое и всестороннее изучение экономической информации о функционировании анализируемого субъекта хозяйствования с целью принятия оптимальных управленческих...
Образование соседних чисел Фрагмент:
Программная задача: показать образование числа 4 и числа 3 друг из друга...
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|
Тема 2: Анатомо-топографическое строение полостей зубов верхней и нижней челюстей. Полость зуба — это сложная система разветвлений, имеющая разнообразную конфигурацию...
Виды и жанры театрализованных представлений
Проживание бронируется и оплачивается слушателями самостоятельно...
Что происходит при встрече с близнецовым пламенем
Если встреча с родственной душой может произойти достаточно спокойно – то встреча с близнецовым пламенем всегда подобна вспышке...
|
|

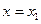 до
до 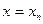 c шагом
c шагом 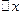 . При выполнении задания использовать операторы цикла с постусловием, с предусловием и оператор цикла с параметром.
. При выполнении задания использовать операторы цикла с постусловием, с предусловием и оператор цикла с параметром.