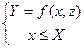Часть I – Общие понятия моделирования.
И.о директора ИНиГ В.А. Гридин Список рекомендуемой литературы 1. Прудковский Б.А. Зачем металлургу математические модели? – М.: Наука, 1989 – 191 с. 2. Р. Шеннон. Имитационное моделирование систем: искусство и наука.–М.: «МИР», 1978, 418с. 3. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М: Изд-во «Наука», 1976, 279 с. 4. Е.С. Вентцель. Исследование операций. Задачи, принципы методология. – М.: Наука, Главная редакция физико-математической литературы, 1980. – 208 с. 5. Норенков И.П. Основы автоматизированного проектирования: учебник для вузов. – М.: Издательство МГТУ имени Баумана, 2002. – 336 с. 6. Лабораторные работы (4 у дневников, 3 у вечерников) Экзамен (Зачет у вечерников) Часть I – Общие понятия моделирования. Лекция 1 Введение Элементы моделирования использовались с самого начала появления точных наук, поэтому некоторые методы моделирования основываются на математических методах вычислений заложенных еще Ньютоном и Эйлером, а слово “алгоритм” происходит от имени средневекового арабского ученого Аль-Хорезми. Второе рождение моделирование пережило в конце 40-х – начале 50-х годов XX века, что обусловлено двумя причинами. Во-первых, появление компьютеров позволило значительно расширить возможности этого направления в науке за счет освобождения исследователя от большого количества повторяющихся действий выполняемых в процессе моделирования. Во-вторых, в это время появляется большое количество задач, осуществление которых на практике невозможно к таким задачам в первую очередь следует отнести национальные программы СССР и США по созданию ракетноядерного щита и космические программы. Невозможно представить современное производство без широкого применения моделирования. Практически на любом этапе производства, начиная от создания эскизного проекта и заканчивая контролем качества готового издания, мы сталкиваемся с понятиями модели и моделирования. Что же такое моделирование и в чем оно заключается? Моделирование (процесс создания модели) заключается в замене исходного объекта его “образом” моделью. В дальнейшем полученная модель при необходимости может быть исследована. Таким образом, среди задач моделирования можно выделит две основные группы задач – прямую и обратную. Прямые задачи отвечают на вопрос: что будет, если в заданных условиях мы примем какое-то решение из множества возможных решений? В частности, в какой будет зависимость изменения толщины прокатываемой ленты при изменении жесткости валков прокатного стана. Для решения такой задачи строиться математическая модель, позволяющая выразить одну или несколько исследуемых величин, т.е. в нашем случае зависимость, связывающая изменение толщины прокатываемой ленты от жесткости валков прокатного стана. Обратные задачи отвечают на вопрос: как выбрать единственное решение из множества решений, так чтобы интересующая нас величина была оптимальной. Например, какой будет интервал изменения толщины ленты, если жесткость валков прокатного стана будет равна заданной величине. Обратные задачи называются задачами оптимизации. Естественно, что прямые задачи проще обратных, поскольку для решения ряда обратных задач зачастую приходиться сначала решить прямую задачу. На современном этапе развития общества процесс моделирования очень тесно связан с использованием ЭВМ. Это объясняется рядом причин, среди которых можно выделить следующие: · большое количество повторяющихся действий выполняемых исследователем, например, при моделировании процесса штамповки поковки зубчатого колеса из цилиндрической заготовки для определения деформации с помощью метода конечных элементов необходимо выполнить сотни, тысячи одинаковых операций; · доступность для математического описания и представления в машинном виде большинства методов используемых в моделировании; · возможность представления результатов моделирования в наиболее полном и наглядном для исследователя виде; · возможность глубокого и всестороннего изучения моделируемого объекта или процесса производства. Расходы на производство обычно строго регламентированы и очень часто является не целесообразно проводить дополнительные эксперименты с тем, чтобы изучить влияние всех факторов на производственный процесс более детально. В условиях компьютерного моделирования фактически регламентируется только время работы над проектом, поэтому есть возможность провести более полное исследование; · возможность получения результатов, получение на практике которых дорого, долго и невозможно. Неудивительно, что методы моделирования в металлургии бурно развиваются, охватывая все новые сферы этой области науки. Степень использования моделирования в производственном процессе говорит об уровне самого производства. Там где большую часть подготовки к производству занимает исследование и изучение свойств будущего изделия там соответственно и выше качество изготавливаемого изделия. Соответственно и требования к инженерам, обеспечивающим проектирование подобного изделия предъявляться более высокие.
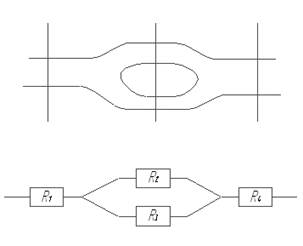
Основные используемые понятия и определения. Металлургия - это отрасль промышленности, охватывающая процессы получения металлов из руд, а также процессы, сообщающие металлическим сплавам путем изменения их химического состава свойства, соответствующие назначению. К металлургии относятся процессы обработки руд с целью их подготовки к извлечению металлов, процессы извлечения металлов из руд, очистка металлов от нежелательных примесей (рафинирование), производство металлов и сплавов, термическая, химико-термическая и термомеханическая обработка металлов, обработка металлов давлением и литьем, покрытие в декоративных или защитных целях поверхности изделий из металла слоями других металлов /Источник????/. Обработка металлов давлением – процесс изменения исходной заготовки под воздействием деформирующего инструмента. При этом в качестве заготовки могут использоваться различные металлические объекты. Моделирование – это процесс построения моделей объектов, процессов или явлений и их дальнейшего исследования и изучения. Модель – это представление объекта или процесса в виде удобном для исследования и изучения. Модель может использоваться для объяснения, и понимания явлений окружающего мира. Как правило, модель отражает некоторые характерные свойства объекта в абстрактной форме. Модель может служить инструментом для сравнения альтернативных решений использование, которого позволяет принять решение о том какому из вариантов отдать предпочтение. Использование модели позволяет повысить эффективность работы с объектом исследования. Так что же может являться моделью? Может ли математическая формула быть моделью объекта? Все зависит от того, какие цели ставит перед собой следователь. Например, степенная зависимость упрочнения материала используемая для решения задач в пластической области деформирования материала не даст ответа на вопрос о том, как себя ведет материал в упругой области нагружения и соответственно не может являться моделью. В любом случае нужно помнить то, что любая модель не может абсолютно точно описывать объект, она лишь дает приближенное представление о поведении объекта или процесса. Нужно также помнить и то, что один и тот же процесс всегда может быть описан несколькими моделями. Процесс – это определенная последовательность действий, приводящих к достижению цели (например, технологический процесс). Основное отличие процесса от явления заключается в том, что совокупность последовательно протекающих явлений образуют процесс. Процессы могут быть различны по своей природе. По степени участия человека все процессы можно разделить на две группы – управляемые и неуправляемые. Среди управляемых человеком процессов можно выделить производственные процессы или процессы, направленные на получение конкретного результата труда. Мы будем рассматривать только ту часть производственных процессов, которая содержит целенаправленное действие по изменению состояния предмета труда или другими словами – технологический процесс. В каждом производственном процессе можно выделить центральный технологический процесс, который соответствует специализации производства. Поскольку технологический процесс состоит из последовательности законченных действий, то внутри технологического процесса можно выделить технологические операции т.е. технологический процесс это законченная последовательность технологических операций. Различают технологические операции обработки, транспортировки и контроля. Основные процессы черной металлургии согласно /Прудковский/ приведены на рис. 1.
Рис. 1 – Основные процессы черной металлургии. Для описания технологического процесса используется понятие технологического параметра. Под технологическим параметром мы будем понимать любой параметр, определяющий результат технологического процесса. Объект – в это отдельный элемент, рассматриваемый с точки зрения моделирования, в металлургии им может быть отдельная единица оборудования, инструмент, цех, предприятие. Фактор –
Лекция 2 Основные подходы в моделировании. Под подходом в моделировании мы будем называть общее направление создания модели. Очень часто на основании используемого подхода осуществляется классификационное деление моделей. Для построения моделей можно использовать два подхода: гносеологический и кибернетический (или информационный) /Беленький/. Гносеологический подход позволяет получить математическое описание процесса на основе теоретического анализа физических процессов, происходящих в исследуемом объекте с учетом особенностей и характеристик обрабатываемого материала. Постановка эксперимента при использовании данного подхода осуществляется только для уточнения и проверки уже построенной модели. Построенные на основании данного подхода модели являются наиболее полными и используются для решения задач по выяснению механизма явлений протекающих в объекте. После аппроксимации простыми зависимостями эти модели можно использовать в задачах оптимизации и автоматического управления. Кибернетический подход – базируется, на изучении входных и выходных переменных кибернетической системы, которую называют “черным ящиком” (рис.2). “Черный ящик” представляет собой систему связей, недоступную для наблюдения, т.е. неизвестен характер связи входов Х и выходов Y участвующих в процессе /Норенков/.
Рис. 2 – Схема “черного ящика”: Х – информация поступающая на вход; Y – информация поступающая на выход.
Данный подход дает математические модели, которые описывают поведение объекта, а не описывают его физической сущности. Модели, построенные на основании данного подхода, используются для оптимизации и автоматического управления. Рассмотрим пример использования гносеологического и кибернетического подходов. Допустим, что необходимо исследовать какое влияние на изменение толщины фланца стаканчика в ходе процесса вытяжки оказывают величина исходного диаметра заготовки. Напомним, что процесс вытяжки заключается в получении стаканчика из плоской исходной заготовки рис. 3. В соответствии с кибернетическим подходом необходимо провести серию экспериментов и для получения исходных данных. Полученные из экспериментов данные математически обработать и выяснить есть ли между исходным диаметром заготовки и толщиной фланца зависимость или нет. В случае если зависимость наблюдается необходимо провести дополнительное исследование полученной модели с тем, чтобы установит характер силу и поведение этой зависимости.
Рис. 3 – Вытяжка цилиндрической детали из круглой плоской заготовки: 1 – матрица; 2 – заготовка; 3 – пуансон. В соответствии с гносеологическим подходом необходимо провести теоретическое исследование процесса вытяжки. Для этого можно обратиться к теории листовой штамповки. Согласно теории листовой штамповки надо воспользоваться уравнением связи напряжений и деформации для случая плосконапряженного состояния, уравнением определяющим меридиональное напряжение без учета упрочнения и трения и условием постоянства объема /Попов/:
После математических преобразований можно вывести соотношение:
Основываясь на этом соотношении можно примерно оценить толщину верхней кромки полученного стаканчика. В случае использовании данного подхода моделирования решение было получено “на бумаге” и практически все затраты сводятся лишь к затратам времени на теоретическое исследование. Виды моделей (доб примеры из ОМД) Модели можно классифицировать различными способами. При этом практически все классификации ориентированны на конкретные задачи и поэтому достаточно сильно отличаются друг от друга. Укажем некоторые типовые группы моделей, которые могут быть положены в основу системы классификации /Норенков, Рыжиков, Прудковский стр. 39 Капустин, Шеннон стр19/. Как отмечалось выше классификационное деление может осуществляться на основе используемого подхода моделирования или вида решаемой задачи прямой или обратной (оптимизационной). Среди оптимизационных задач также можно выделить задачу одноразовой и текущей оптимизации. Если задачу необходимо решить один раз, то в этом случае говорят о задаче одноразовой оптимизации. В случае если исследуемый процесс является нестационарным или условия его проведения постоянно изменяются, то имеет место задача текущей оптимизации /Беленький стр. 5-6, Адлер/ Модель можетбытьреальным физическим объектом – физическая модель (макет, стенд) или моделью спецификацией т.е. условным существующем на “бумаге” объектом обладающим интересующим исследователя свойствами. Среди физических моделей можно выделить следующие группы: в зависимости от учета фактора времени статические и динамические; по силе использования физической аналогии: натурные, масштабные и аналоговые; в зависимости от поставленных задач: демонстрационные, экспериментальные и т.д. в зависимости от количества используемых измерений: одно-, двух-, трехмерные. Статические физические модели помогают нам наглядно представить себе пространственные соотношения. Их примером могут быть макеты заводских сооружений, или макеты сложной штамповочной оснастки. Динамическая физическая модель должна учитывать время или развитее процесса во времени. Примером динамической физической модели может служить модель штамповочного участка, предназначенная для подготовки нового технологического процесса к внедрению данного процесса на заводе. Физические модели могут быть натурными – полномасштабными макетами (опытные образцы для штамповки), или масштабными – выполняемыми в уменьшенном или увеличенном масштабе, (например, модель кристаллической решетки, модель атома). Отличительной особенностью любой натурной и масштабной физической модели является то, что она “выглядит” подобно моделируемому объекту. Аналоговыми моделями являются модели, у которых изучаемое свойство реального объекта заменяется аналогичным по поведению свойством другого объекта. Как правило, эта задача решается заменой свойств моделируемого объекта свойствами модели, после чего полученные результаты рассматриваются применительно к исходным свойствам моделируемого объекта. Например, необходимо оценить качество заполнения опоки при литье детали показанной на рис. 4. Это можно сделать заменой формы опоки на электросопротивление проводников в цепи с током. Для этого форму опоки можно разбить на несколько участков, каждый из которых заменить проводником с определенным электросопротивлением. Причем для замены каждого участка электросопротивление подбирать относительно размеров и формы опоки на данном участке. В этом случае оценку качества заполнения опоки можно дать по течению в проводнике электрического тока.
Рис. 4 – Пример аналоговой модели: а – опока; б – аналоговая модель опоки.
Физические модели могут быть также одномерными, двумерными и трехмерными, а также использоваться как для демонстрационных целей (например, глобус) так и для проведения косвенных экспериментов. Например, генеральный план завода являются примером двумерной физической модели в уменьшенном масштабе, используемой для целей экспериментирования. Среди моделей спецификаций записываемых в письменном виде наиболее распространены математические модели – модели, описанные с помощью средств математики. Математические модели могут быть геометрическими, динамическими, логическими и т. д., в зависимости от того какие интересующие свойства они отражают. Математические модели могут быть символическими, численными и смешанными, в зависимости от того используется обозначение величины или ее численное значение. Математические модели можно разделить на две группы: аналитические и алгоритмические (функциональные). Аналитические модели являться явно выраженными зависимостями между входными данными и исследуемыми свойствами, в то время как в алгоритмических моделях эта связь задананеявно, а в виде алгоритма. Можно сказать, что аналитические модели это частный случай алгоритмических, когда алгоритм вычисления сведен к расчету одного уравнения /Норенков/. Другой частный случай алгоритмических моделей это имитационные модели, они отображают процессы в системе при наличии внешних воздействий на систему. Имитационная модель – это алгоритмическая поведенческая модель. Данные модели используются для имитации процессов и объектов, осуществление которых на практике проблематично в связи с высокой стоимостью постановки эксперимента длительностью процесса, сложностью объекта или другими причинам. При рассмотрении иерархических уровней математических моделей металлургического производства можно выделить следующие уровни: микроуровень, макроуровень, и метоуровень. /Капустин, Прудковский/. Особенностью модели на микроуровне является отображение физических процессов в непрерывном пространстве и времени. С помощью дифференциальных уравнений в частных производных рассчитываются поля напряжений и деформаций. Объектами исследования на этом уровне являются отдельные технологические операции. На макроуровне используют укрупненную дискретизацию производства по функциональному признаку, т.е. используют обыкновенные дифференциальные уравнения. В этих моделях обычно иметься две группы переменных – независимых (время) и зависимых (фазовых). В качестве фазовых переменных выступают силы, скорость перемещения, напряжения и т.д. В качестве объектов исследования выступают целые технологические процессы. Объекты на метоуровне описывают укрупнено. В качестве математического аппарата используются обыкновенные дифференциальные уравнения, теория массового обслуживания, и т.д. Объектами выступают уже целые технологические системы. Среди моделей спецификаций можно также выделить статические и динамические, детерминированные и стохастические, аналоговые и дискретные модели. Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы во времени. Стохастические и детерминированные модели различают в зависимости от учета или не учета случайных факторов. В детерминированных задачах вероятность совершения исследуемого события всегда равна 100% в то время как в стохастических задачах эта вероятность может изменяться или даже быть неизвестной. /Вентзель/ В аналоговых моделях переменные величины являться непрерывными, в дискретных – дискретными. Важным частным случаем дискретных моделей являются логические или булевы модели, в них состояние системы и ее элементов описывается булевыми величинами. В ряде случаев применяют смешанные по этому признаку модели. В них одна часть системы описывается аналоговыми моделями, другая - дискретными. В дальнейшем мы будем говорить, только о функциональных математических детерминированных моделях используемых для расчета на ЭВМ называя их просто моделями или математическими моделями.
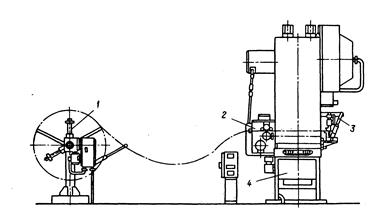
Лекция 3 Формализация объектов и процессов. Адекватность модели. Для того чтобы использовать ЭВМ в процессе моделирования необходимо, чтобы исходный объект или процесс был формализован, т.е. описан математическими зависимостями. Построение математического описания объекта или процесса называют формализацией процесса. В ходе процесса формализации происходит описание исходного объекта с заданной точностью. Следует заметить то, что даже небольшие участки реального мира слишком сложны, для того чтобы их можно было полностью описать. Любая задача может включать в себя огромное число переменных, параметров, элементов, соотношений, ограничений и т. д. Соответственно и при построении модели, в нее можно включить бесконечное число элементов, что значительно усложнит процесс поиска верного варианта решения. Следовательно, при создании модели необходимо пренебречь частью реальных характеристик изучаемого объекта и выделить только те особенности, которые необходимы для описания идеализированного варианта реального объекта или процесса. При оценке процессов и объектов металлургии можно воспользоваться правилом Паретто справедливым для большинства технических систем. Правило Паретто заключается в том, что на интересующие исследователя характеристики системы оказывает существенное влияние лишь несколько из множества факторов. Как правило, 20% факторов определяют 80% интересующих свойств, в то время как оставшиеся 80% факторов определяют оставшиеся 20% свойств /Шеннон стр. 182/. Таким образом, важной задачей моделирования является правильный выбор исследуемых факторов, поскольку именно правильное решение этой задачи позволяет значительно сэкономить силы и средства исследователей. Например, очевидно, что в случае моделирования процесса ХХХХХ нет смысла изучать влияние ХХХ на процесс. В большинстве случаев выбор исследуемых факторов осуществляется на основании уже накопленной информации, опыта и интуиции исследователя. Поэтому моделирование является творческим процессом, который может быть сравнен с искусством. Любая модель является упрощением представления реального мира. Если это приближение выполнено правильно, то с помощью модели можно получить верные результаты. Для того чтобы модель была “похожа” на объект необходимо, чтобы выполнялись следующие условия. Во-первых, должно существовать однозначное соответствие между элементами модели и элементами представляемого объекта. Во-вторых, должны быть сохранены точные соотношения или взаимодействия между элементами. При разработке модели систему обычно разбивают на части, т.е. проводят анализ. Анализ необходим для выявления взаимодействия между элементами исследуемого объекта или процесса. Например, в ходе анализа автоматизированного производственного участка листовой штамповки можно выделить отдельные взаимодействующие единицы оборудования (подающее и разматывающее устройство, штамповочный пресс и т.д.) и установить параметры взаимодействия между этими единицами (компенсационный запас материала, частоту включения разматывающего устройства и т.д.) /Михеев/. При необходимости каждую единицу оборудования можно разбить на отдельные механизмы (на штамповочном прессе это может быть механизм подачи, механизм привода ползуна и т.д.), и установить параметры их взаимодействия (например, скорость подачи материала, величину его перемещения и т.д.).
Рис. 5 – Автоматизированный участок листовой штамповки: 1 – разматывающее устройство; 2 – валковая подача; 3 – ножницы для резки отходов; 4 – пресс.
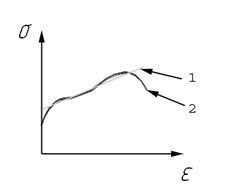
Решая задачу анализа очень часто приходиться сталкиваться с другого рода упрощениями исследуемого объекта. Данное упрощение, как правило, связано с заменой сложного характера зависимости реального объекта на более простую зависимость, используемую при построении модели. Например, при моделировании процессов ОМД зависимость между напряжениями и деформациями кривой пластичности часто заменяют на более простую линейную зависимость рис 7. В этом случае известно, что зависимость между напряжениями и деформациями является нелинейной, однако если принятое допущение о линейном характере зависимости на взгляд исследователя оправдано (например, если исследование проводиться на участке где линейная зависимость очень точно описывает кривую пластичности см. рис. 6), то мы можем принять данное допущение. Еще одна сторона упрощения связана со сравнением порядка различных величин, фигурирующих в модели. Например, изменение некоторой величины у с течением времени можно описать уравнением вида: у=ах2+вх+с, где у – исследуемая величина, х – переменная определяющая исследуемую величину, а, в, с – параметры уравнения. В случае если а << в и а << с то множителем ах2 можно пренебречь.
Рис. 6 – Иллюстрация к замене кривой пластичности линейным отрезком: 1 – модель; кривая пластичности. После того как отдельные элементы системы были проанализированы и упрощены, очевидно, что необходимо осуществить задачу синтеза модели. Здесь надо учесть, что в ходе синтеза система должна быть собрана корректно, как с точки зрения характера взаимодействия, так и с точки зрения соединения объектов. Другими словами при передаче информации от одной части системы к другой передача должна осуществляться в одинаковом виде и в правильной последовательности. При этом недолжно происходить потерь информации. Например, на этапе анализа было выяснено, что на диаграмму σ-ε можно разделить на два участка упругий и пластический и что каждый из участков можно заменить линейными зависимостями, с устраивающей исследователя точностью. Тогда на этапе синтеза необходимо объединить уравнения этих прямых в одну систему таким образом, чтобы полученная система полностью определяла исследуемую зависимость на исследуемом участке. Для этого необходимо найти точку пересечения этих прямых. Полученная в результате зависимость носит название билинейного закона.
Рис. 7 – Иллюстрация к задаче синтеза: а – кривая упрочнения: 1 – прямая описывающая пластический участок, 2 – прямая описывающая пластический участок кривой упрочнения; б – билинейный закон. Следует заметить, что прямая описывающая пластические свойства может быть неограниченна справа по оси деформаций. Однако при удалении по оси деформаций в направлении увеличения деформаций от точки в достоверность описания прямой пластического участка кривой упрочнения становиться ниже, поэтому необходимо ввести критерий позволяющий судить о возможности использования принятой модели. Для оценки соответствия модели и исследуемого объекта или процесса существует понятие адекватности (достоверности). Существует несколько аспектов проверки адекватности. Во-первых, сама модель должна быть непротиворечивой и подчиняться законам логики. Во-вторых, достоверность модели во многом зависит от способности правильно описывать исходную ситуацию. Однако ответ на вопрос о том, успешно ли проходит предложенная модель такую проверку, в значительной степени субъективен. Модель может отражать действительность, при этом она не является действительностью. При получении достоверного решения нужно помнить о том, что улучшение решения для модели, должно быть оправдано, прежде всего, самой постановкой задачи. В первую очередь это касается точности имеющихся данных. Если исходные данные известны с погрешностью 10% (большинство задач ОМД), то смысла искать решение с точностью 1%, нет. В этом случае можно сказать – “всякое уравнение длиной более двух дюймов, скорее всего, неверно!” /Шеннон/. При оценке достоверности необходимо помнить также и о затратах времени и ресурсов связанных с получением более точного решения. Порой менее точное решение, полученное своевременно может дать больше выгоды. Например, для получения быстрого решения при моделировании процесса вытяжки в программе AutoForm предусмотрен специальный модуль, который позволяет получить приближенное решение задачи и оценить с технологической точки зрения возможность изготовления изделия. На основании полученного решения у компании, использующей программу AutoForm, есть возможность быстро ответить потенциальному заказчику сможет ли она изготовить изделие и какова будет его примерная стоимость изготовления. В заключение еще раз следует сказать то, что математическая модель представляет собой упрощение реальной ситуации. “Ощутимое упрощение наступает тогда, когда несущественные особенности ситуации отбрасываются и исходная сложная задача сводится к идеализированной задаче, поддающейся математическому анализу” /Эндрюс/.
Требования предъявляемые к моделям. Моделирование всегда связано с решением конкретных задач, поэтому и конечные результаты должны отражать истинное положение вещей. В этом смысле построенная модель не должна давать абсурдные результаты. Желательно чтобы была возможность изменения величины ее параметров и переменных в как можно большем интервале измерений, поскольку это позволяет ее изучить на всю глубину исследуемых параметров. Желательно также чтобы модель могла ответить на вопрос – “а что, если...?”, поскольку именно этот вопрос позволяет ее изучить наиболее полно. Необходимо также помнить о том для кого предназначается информация, которая появляется при моделировании. Нет смысла разрабатывать модель, если ей в конечном итоге не сможет воспользоваться пользователь, для которого она предназначалась. При построении модели надо также учитывать и тот факт что со временем ситуация может измениться и разрабатываемая модель должна иметь возможность адаптироваться (подстроиться) к новым условиям. Изменения могут быть связаны как с изменением интервала значений уже рассматриваемых параметров, так и с появлением новых значимых параметров. Следовательно, и модель должна иметь возможность к подобной адаптации. Конечно же, модель должна быть экономичной. Экономичность модели определяется, как затратами, затрачиваемым пользователем модели на ее использование, так и возможностью быстрого перестроения модели исследователем. Основываясь на вышеизложенном можно сформулировать основные требования предъявляемые к модели. Модель должна быть: · точной – обеспечивающей совпадение результатов эксперимента полученных от реального объекта с данными, полученными от модели; · экономичной; · целенаправленной – не содержащей лишней, ненужной информации; · полной с точки зрения возможностей решения главных задач; · адаптивной, позволяющей легко переходить к другим модификациям или обновлять данные, · простой и понятной для использующего модель пользователя. Для того чтобы моделью можно было пользоваться, при ее разработке должны быть тщательно продуманы и потребности, и психология ее конечного потребителя.
Лекция 4. Общий вид математических моделей. Пример+ Норенков!!! Напомним что такое математическая модель. Математическая модель, это модель, которая в общем случае представляет собой записанный с помощью средств математики алгоритм вычисления вектора выходных параметров Y при заданных входных параметрах X. В дальнейшем мы будем рассматривать только аналитические модели, в которых зависимость параметров между собой выражена в явном виде. Математические модели предназначены для отображения физических или информационных процессов, протекающих в объектах в ходе технологического процесса. Обычно данные модели представляют систему уравнений, описывающих внутренние, внешние и выходные параметры. В самом простом случае структуру аналитической модели мы можем представить математически в виде следующей системы:
где Y=f(x,z) – целевая функция, х≤Х – ограничение, Y – результат действия системы; х, z – переменные и параметры; f – функциональная зависимость между параметрами и переменными определяющая величину Y. Данная система содержит одну целевую функцию и одно ограничение, в общем случае математическая модель может содержать несколько целевых функций и несколько ограничений. Тогда любая математическая модель может содержать следующие составляющие /Шеннон/: — компоненты, — переменные, — параметры, — функциональные зависимости, — ограничения, — целевые функции. Под компонентами понимают составные части, образующие систему. В качестве компонентов могут выступать ограничения и целевые функции. Иногда под компонентами понимаются элементы системы или ее подсистемы. Например, если в качестве системы рассматривать технологический процесс, то компонентами этой системы будут отдельные операции. Полное количество компонентов участвующих в моделировании выбирается исследователем. Параметры это величины, выбирающиеся произвольно в отличие от переменных, которые принимают только значения, определяемые видом используемой функции, т.е. параметры являются постоянными величинами, не подлежащими изменению. Например, в законе Гука (1): Е является параметром, а σ; и ε; — переменными. σ=Еε;, (1) где σ; – напряжения, Е – модуль Юнга, ε – деформации. Переменные могут быть двух видов - внутренними и внешними. Внешние переменные называют также входными, поскольку они являются результатом воздействия внешних причин. Переменные, возникающие в системе, называются внутренними. Они появляются в результате воздействия внутренних причин. Внутренние переменные могут быть переменными состояния, если они характеризуют состояние или условия, имеющие место в системе или выходными переменными, если они описывают состояние на выходах системы /Шеннон/. Функциональные зависимости характеризуют переменные и параметры в пределах компонента или выражают соотношения между компонентами системы. Эти соотношения, могут быть различными по своей природе и используемому математическому аппарату. По природе исследуемого объекта соотношения могут быть детерминистскими, или стохастическими. Детерминистские соотношения – это уравнения устанавливающие зависимость между переменными или параметрами в случае, когда процесс однозначно определен. С тохастические соотношения однозначно не определяются с помощью входных параметров. Функциональные зависимости могут быть получены в соответствии с двумя подходами: гносеологическим или информационным. Как правило, стохастические соотношения между входными и выходными переменными характерны для информационного подхода. Добб. Выбор функциональной зависимости. Ограничения являются математической записью пределов изменения значений переменных. Они могут быть поставлены разработчиком – искусственные ограничения, или природой исследуемых объектов в соответствии с присущими ем свойствами – естественные ограничения. Как правило, искусственные ограничения являются техническими требованиями к объекту или процессу. Например, требование предьявляемое к поковке по штамповочному уклону служит ограничением при моделировании процесса заполняемости штампа при штамповке. Примером естественного ограничения может быть максимальное и минимальное значение процентов содержания компонента сплава изменяемое от 0 до 100%. В качестве примера искусственного ограничения можно привести ограничения связанные с поиском сплава с наибольшей прочностью при изменении процентного содержания одного из компонентов в диапазоне от 10 до 25%. Целевая функция, или функция критерия, - является отражением целей или задач моделирования. Уравнение целевой функции должно быть, как можно более точно определено относительно целей задач исследования. Под критерием понимается конкретная мера оценки позволяющая давать верное суждение о суть происходящих явлений. Такое определение критерия объясняется двумя причинами. Во-первых, выбор критерия влияет на процесс создания модели и работу с ней. Во-вторых, неправильное определение критерия обычно ведет к неправильным заключениям. Функция критерия (целевая функция) является основой модели. Практически процесс исследования модели и решения задачи оптимизации полностью связан с исследованием целевой функции. В зависимости от сложности поставленной задачи математическая модель может содержать несколько целевых функций, в этом случае говорят, что задача моделирования является многокритериальной. Добб. Требования к целевой функции.
Основные этапы формализации объектов и процессов при построении модели. Не зависимо от того в соответствии, с каким подходом гносеологическим или информационным осуществляется построение модели, процесс создания формализованной модели будет содержать следующие этапы: 1. постановка задачи, 2. анализ и упрощение данных, 3. синтез структуры модели, 4. проверка адекватности модели, 5. принятие решения о доработке модели или ее использовании. На первом этапе необходимо определить, в чем именно заключается задача формализации, и какие результаты необходимо получить за счет изменения каких параметров. На втором этапе исследователю необходимо на основании анализа элементов упростить реальный объект или процесс и поставить ограничения. Процесс упрощения достаточно подробно изложен в пункте формализация объектов и процессов в металлургии. Как правило, при постановке ограничений для установления области исследования пользуются здравым смыслом (например, при моделировании свойств нового сплава состоящего из большого количества компонентов содержание любого из компонентов не может быть более 100%). В другом случае ограничения могут быть сформулированы при постановке задачи (например, постановка задачи звучит следующим образом: уточнить концентрацию компонента в сложном сплаве в интервале от 10 до 15% так чтобы прочность сплава была наибольшей). Создать математическое описание элементов модели. На третьем этапе, на основании уже формализованных данных создается сама модель. Этот этап можно разделить на две части. Во-первых, записывается сама модель (система уравнений) без конкретизации числовых значений используемых параметров. Эта часть синтеза структуры математической модели может осуществляться с помощью классического или системного подхода. Во-вторых, осуществляется расчет и уточнение числовых значений ранее записанной модели. На четвертом этапе осуществляется проверка адекватности построенной модели (смотри пункт формализация объектов и процессов в металлургии). На этом этапе желательно осуществить постановку эксперимента с целью подтверждения созданной модели. На пятом этапе, на основании теоретической или экспериментальной проверки принимается решение о доработке модели или ее использовании. В случае если для моделирования использовалось несколько различных вариантов моделей производить выбор наиболее подходящего варианта. Добб. Критерии выбора из нескольких вариантов.
Лекция 5 Основные этапы компьютерного моделирования. На современном этапе развития науки и техники моделирование очень тесно связано с использованием ЭВМ, а возможности компьютерного моделирования иногда кажутся, настолько большими, что моделирование называют “третьим методом” познания сочетающим в себе достоинства как теории так эксперимента /Эдвардс??/. Задачи компьютерного моделирования условно можно разделить на две группы: во-первых, это задачи использования уже имеющегося программного обеспечения и, во-вторых – “классические” задачи создания и использования нового программного обеспечения. В соответствии с целями моделирования разработка программы может осуществляться как для конкретного технологического процесса, так и для целой группы технологических процессов или даже способов. Например, к первой группе можно отнести задачу расчета деформации валков прокатного стана заданной модели для прокатки полосы толщиной 10 мм из технически чистого алюминия. Ко второй – задачу описания всех известных способов ковки и объемной штамповки. В “классическом” варианте постановки вопроса о моделировании какого-либо объекта или процесса можно условно выделить три этапа: - создание формализованной модели, - создание алгоритма, - создание программы На первом этапе собирается информация об исходном объекте, которая позволяет получить важ
|



 а)
а)  б)
б)