X2min X2max
Рис. 5. 1. Область определения факторов Чтоб указать значение параметра оптимизации, нужна еще одна ось. Если ее ввести, то поверхность отклика будет выглядеть следующим образом (Рис. 5.2).
Рис. 5.2. Поверхность отклика Пространство, в котором строится поверхность отклика, будем называть факторным пространством. Оно задается координатными осями, по которым откладываются значения факторов и параметра оптимизации. При многих факторах поверхность отклика уже нельзя изобразить наглядно и приходиться ограничиваться только алгебраическим языком. При двух факторах можно ограничиться плоскостью для изучения факторного пространства. Для этого надо произвести сечение поверхности отклика плоскостями параллельными плоскости Х1ОХ2 и полученные в сечениях линии спроектировать на эту плоскость. Каждая линия соответствует постоянному значению параметра оптимизации. Такая линия называется Линией равного отклика (Рис.5.3).
Рис. 5.3. Проекция сечений поверхности отклика на плоскость
Существует соответствие между состоянием «черного ящика» и значением параметра оптимизации – каждому возможному состоянию «ящика» соответствует одно значение параметра оптимизации. Обратное, строго говоря, неверно. Итак, представляя поверхность отклика возвращаемся к основному вопросу: как ставить эксперимент, чтобы найти оптимум при минимуме затрат. Можно рассмотреть следующие возможности (2 из 3 возможностей будут даны в Лабораторной работе №2): 1.Мы располагаем таблицей, в которой содержатся все возможные состояния объекта и соответствующие им отклики. И мы выбираем то или те состояния, которые соответствуют наилучшему отклику. Недостаток: огромное количество состояний. Пример: нахождение оптимального положения канала на матрице. 2.Случайный выбор некоторого числа состояний и определение откликов в них, надеясь, что среди них попадутся оптимальное или близкое к нему состояние. 3.Строить мат. модель, чтоб с ее помощью предсказывать значения откликов в тех состояниях, которые не изучались экспериментально. Если мы не можем измерить отклик в каждом состоянии, то хоть сумеем предсказать результат. Причем нам интересны не все состояния, а лишь те, которые приближают нас к оптимуму. Такая стратегия приводит нас к пошаговому принципу, лежащему в основе метода ПЭ. Шаговый принцип Итак, за отказ от полного перебора надо чем-то платить. Цена – это предположения, которые следует сделать относительно свойств неизвестной нам модели до начала эксперимента (априорные положения). Некоторые из предположений мы никогда не сможем проверить. Такие предположения называются постулатами. Если реально они не выполняются, то, возможно, что мы найдем не оптимум (хотя найденное может нас устроить). Какие предположения о свойствах поверхности отклика мы делаем? Главное – это непрерывность и гладкость поверхности, и наличие единственного оптимума (Рис. 5.4).
Y Y
   
Рис. 5.4. Примеры функций отклика для одного фактора
(Объяснить разницу в нахождении оптимумов для функций слева и справа) Итак, если предпосылки выполняются, а мы будем знать значения параметра оптимизации в нескольких соседних точках факторного пространства, то мы сможем представить себе результаты, которые можно ожидать в других соседних точках. Значит можно найти такие точки, для которых ожидается наибольшее увеличение (или уменьшение) параметра оптимизации. Тогда ясно, что следующий эксперимент надо переносить именно в эти точки. Надо продвигаться в этом направлении, минуя остальные. Сделав новый эксперимент, снова можно (и нужно) оценить направление, в котором, скорее всего и следует двигаться. В силу единственности оптимума мы, таким образом, рано или поздно его достигнем. Это и есть пошаговый принцип. Пример использования шагового принципа Рассмотрим и сравним два варианта поиска оптимума для одой и той же поверхности (Рис.5.5). В случае а) использован классический подход (метод Гаусса - Зейделя). Он состоит в том, что сначала последовательно изменяются значения одного фактора. Находится и фиксируется наилучшее значение этого фактора. Затем последовательно изменяются значения второго фактора и т.д. если их больше двух.
а) б) Рис. 5.5. Два способа поиска оптимума В случае б) представлен простейший вариант шаговой процедуры. Сначала изучается локальная область (1), затем определяется наиболее интересное направление и в этом направлении ставятся следующие опыты. Следует сказать, что эффективность процедуры зависит от выбора начальной точки и вида поверхности (Рис.5.6.).
а) б) Рис.5.6. Пример эффективности процедур при нахождении оптимума
Итак, возвращаясь к проблеме выбора модели, мы определяем главное требование к модели, а именно – способность предсказывать направление дальнейших опытов с требуемой точностью. Так как до получения модели мы не знаем, какое направление нам понадобиться, то естественно требовать, чтоб точность предсказания во всех возможных направлениях была одинакова. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического значения больше, чем на некоторую заранее заданную величину. Модель, которая удовлетворяет такому требованию, называется адекватной. Проверка выполнимости этого требования называется проверкой адекватности модели. Для проверки разработаны специальные статистические методы. Если несколько различных моделей отвечают нужным требованиям, то следует предпочесть самую простую. Пример: на Рис.5.7. изображена логарифмическая функция. На отрезке (Хмин, Хмакс) она с достаточной точностью описывается двумя уравнениями: у= log X и y=bX. Какое из них проще?
Рис.5.7. График логарифмической функции
Примем решение: при прочих равных условиях всегда выбираем (предпочитаем) степенные ряды. Фактически мы выбрали класс моделей. Полиномы различаются максимальными степенями входящих в них переменных. Для случая 2-х факторов это будут следующие полиномы: Полином 0-ой степени: y=b0 Полином 1-ой степени: y=b0+b1x1+b2x2 Полином 2-ой степени: y=b0+b1x1+b2x2+b12x1x2+b11x12+b22x22 Полином 3-ей степени:y=b0+b1x1+b2x2+b12x1x2+b11x12+b22x22+b112x12x2+b122x1x22+b111x13+b222x23 Итак, мы представили неизвестную нам функцию отклика полиномом. Операция замены одной функции другой, в каком то смысле эквивалентной функцией, называется аппроксимацией. Значит, мы аппроксимировали неизвестную функцию полиномом. Но встает вопрос – полином, какой степени взять на первом шаге? Эксперимент нужен только для того, чтоб найти численные значения коэффициентов полинома. Поэтому, чем больше коэффициентов, тем больше опытов окажется необходимым. Мы же стремимся сократить их число. Значит, следует брать такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявляемым к моделям.
Лекция 13 Поиск оптимального решения (обратная задача моделирования). Под решением задачи оптимизации понимается нахождение такого значения входного параметра, при котором значение целевой функции должно быть оптимальным с точки зрения поставленных исследователем задач. Для определенности в нашем случае примем оптимальным такое значение входного параметра, при котором значение целевой функции будет минимально. Прежде всего для решения задачи оптимизации необходимо определить интервал в котором будет изменяться х т. е. поставить ограничения для аргумента функции у=у(х). Как правило, этот интервал задается условиями производства или постановки эксперимента, например, ограничением может быть скорость движения деформирующего инструмента. В этом случае задача по нахождению оптимального значения при известной зависимости между х и у будет сводиться к задаче поиска локального экстремума функции. В зависимости от исходной информации (регрессионного уравнения) могут быть различные варианты решения задачи оптимизации наглядно эти варианты представлены на рис.5. На рис.5 а показан случай когда оптимальное совпадает с экстремальным значением и лежит внутри интервала х1 и х2. Экстремальное значение будет иметь точка на оси х в которой скорость изменения функции у(х)=0, однако оптимальной (минимальной в нашем случае) будет экстремальная точка только на рис.5а а на рис.5б значение функции больше чем на границе интервала [х1;х2]. На рис.5в показан случай когда в интервале [х1;х2] функция у(х) имеет несколько экстремальных значения поэтому для определения оптимального значения также необходимо провести оценку регрессионной зависимости в рассматриваемых точках и на границах интервала. На рис.5 г и д представлены случаи когда экстремальное значение не попадает в рассматриваемый интервал. Очевидно, что в данном случае оптимальным будет значение на границе интервала.
Рис.5 – Варианты решения задачи оптимизации. Симплекс метод Общие понятия симплекс метода. Симплекс метод или точнее группа методов изначально разрабатывался как развитее идеи планирования эксперимента в постоянно изменяющихся условиях производства. Важно отметить тот факт, что симплекс метод позволяет получить обратную связь от объектов исследования что очень важно для автоматизации производственного процесса это и послужило толчком к развитию данной группы методов. Вскоре основываясь на симплекс методе (СМ) появилось целое научное направление в области исследования процессов и объектов называемое адаптивной автоматизацией. Смысл СМ можно изложить следующим образом на примере геодезического корабля осуществляющего промеры глубин в поиске фарватера. Поиск фарватера осуществляется с помощью лота опускаемого с корабля, когда корабль находиться непосредственно в месте замера глубины. Задачу, стоящую перед исследователями можно поставить так – как с помощью наименьшего количества замеров глубины найти наиболее глубокое место. При этом условимся, что в области исследования геодезистов дно плавно сходиться к наиболее глубокой точке и такая точка на данном участке дна одна. Поскольку с корабля не видно направления, в котором дно более крутое то приходиться последовательно промерять глубину в нескольких направлениях. Конечно, исследователям хочется как можно быстрее достичь глубокого места и соответственно не ставить лишние ненужные промеры, то есть ненужно осуществлять промеры во всех направлениях сразу, а необходимо сконцентрировать свое внимание в одном направлении, двигаясь по которому можно попасть в наиболее глубокое место за наиболее короткий срок. Для определения данного направления геодезистам необходимо обладать какой-то информацией о глубине дна, на основании которой они смогли бы сделать вывод о дальнейшем направлении исследований. Как получить эту информацию? Очевидно, что для ответа на этот вопрос нужно провести замеры глубины. Тогда встает очередной вопрос, а, сколько необходимо производить замеров? Если бы корабль двигался все время в одном направлении (например, от одного берега к другому в поисках наиболее глубокого места), то для определения направления ему достаточно поставить два опыта, если же необходимо осуществить замеры глубины в двух направлениях (найти наиболее глубокий участок дна на всем озере), то исследователю необходимо иметь данные хотя бы о трех точках дна. Получается, что для определения направления движения для постановки дальнейших экспериментов в N мерном факторном пространстве необходимо поставить N+1 эксперимент. Заметим что в отличие от метода Бокса-Уилсона, где на основании серии опытов известно направление для постановки дальнейших экспериментов в СМ известно лишь направления для постановки эксперимента на следующем шаге. Таким образом, для принятия решения о дальнейшем движении в направлении более глубокого участка дна необходимо осуществить замер глубины в трех точках при этом замеры не должны осуществляться на одной прямой, поскольку в этом случае у нас будет избыточная информация об одном направлении и отсутствие информации о другом направлении. Получается, что при поиске наиболее глубокого участка дна озера необходимо осуществлять замеры по вершинам треугольника относительно возможных осей направления движения. Желательно так же чтобы все точки лежали друг относительно друга на одинаковом расстоянии, т.е. треугольник был равнобоким. Таким образом, мы получаем план эксперимента, который задается с помощью координат вершин треугольника. Как мы уже и говорили выше для определения направления движения в N мерном факторном пространстве нужно N+1 экспериментов. В общем случае геометрическая фигура образованная N+1 вершинами и лежащая в пространстве, имеющем N координат называется симплексом. В двухмерном пространстве симплексом является треугольник, в трехмерном – пирамида. Теперь имея данные о трех опытах, геодезисты должны принять решение о дальнейшем направлении движения корабля. Очевидно, что правильным решением будет двигаться в направлении, проходящем через точку, имеющую наименьшую глубину, при этом постановку эксперимента можно поставить в точке тоже равно удаленной относительно двух других точек. В результате такого выбора места новой постановки эксперимента мы получаем как бы отраженную плохую точку относительно противолежащей ей грани треугольника. Данное правило называется правилом отражения. В основе данного правила лежит очевидное предположение о том, что линия, которую можно провести через отраженную (новую) и отражаемую (отбрасываемую) точки совпадает с направлением градиента функции отклика. Описанная последовательность действий легко формализуется и может, заполнена в алгоритм для управления расчетом на ЭВМ. Общие правила расчета СМ. Вернемся к нашим исследователям и посмотрим, каким образом они будут выполнять поставленную передними задачу в соответствии с СМ. В начале для сбора исходной информации необходимо поставить серию из трех опытов и получить значения функции отклика, т.е. глубины. Далее для определения направления движения необходимо сравнить между собой значения функции отклика. Зная наихудшее значение и правило отражения, мы можем найти значения факторов (координаты в которых нужно оказаться кораблю для осуществления следующего замера) и поставить эксперимент с рассчитанными значениями факторов (измерить глубину в месте с рассчитанными координатами).
Для определения значений факторов в месте постановки нового эксперимента, в случае если треугольник равносторонний можно воспользоваться формулой:
где N=k+1 – число точек в исходном симплексе, k – размерность факторного пространства, ХХХ – натуральное значение координаты новой точки для фактора с номером j, ХХХ – натуральное значения координаты фактора в отброшенном опыте. Заметим что, получив новую точку и отбросив старую, мы вновь получаем треугольник (симплекс) к которому вновь можно применить правило отражения. Таким образом, последовательно отражая наихудшую вершину, мы будем двигаться к поставленной цели. Но как определить где наибольшая глубина, по достижению которой можно будет закончить постановку экспериментов? Очевидно, что одним из критериев для “остановки” будет достижение максимального из возможных значений функции отклика. Например, получение функции годного 100%. Вторым критерием для остановки может стать зацикленное движение симплекса вокруг одной из его вершин. В этом случае оптимальное значение очень близко к вершине, вокруг которой осуществляется вращение симплекса.
Признаком подобного зацикливания может быть сохранение одной из вершин симплекса своих значений факторов на протяжении N+1 отражений. В реальном производстве при постановке задачи адаптивного управления, как правило, это и есть критерий достижения оптимального значения исследуемых параметров. Поскольку производственный процесс не останавливается на достижении факторами оптимального значения, то постоянное зацикливание симплекса относительно одной из вершин может говорить о нахождении факторов в оптимальном диапазоне. Как только произойдет изменение внешних условий сказывающихся на процессе, такое, что происходит смещение оптимального значения функции отклика относительно уже установившегося значения факторов так тут же и симплекс начинает двигаться в нужном направлении. В этом и заключается адаптивность данного метода. Теперь давайте обратимся к симплексу, а точнее к расстояниям между его вершинами и постараемся сделать так, чтобы движение в направлении оптимума было, как можно более быстрым и для этого будем увеличивать симплекс в нужном направлении. Очевидно, что в этом случае движение в этом направлении будет осуществляться тем быстрее, чем больше будет увеличение симплекса в нужном направлении. Данный метод нахождения оптимального значения исследуемой модели называется пульсирующим симплекс методом. Помимо пульсирующего симплекс метода существует множество различных симплекс методов основанных на изменении расстояния между вершинами и выборе направления для отображения. Перечислим основные достоинства симплекс метода: • адаптивность – к производственным условиям и ошибкам, возникающим при проведении эксперимента; • легко поддается формализации и удобен для использования на ЭВМ; • совместно с процедурой ранжирования может быть использован для качественной оценки процесса или объекта; • при использовании нет необходимости описывать поверхность отклика с помощью плоскости или иного уравнения, что упрощает расчеты и уменьшает погрешность; • позволяет на каждом шаге при необходимости ввести дополнительную размерность путем введения еще одной вершины симплекса. Например, вначале можно осуществить поиск оптимального значения по двум наиболее значимым факторам, а затем скорректировать поиск с учетом третьего фактора. К недостаткам симплекс методов относят: • ограниченность информации о поверхности отклика; • с уменьшением градиента функции отклика эффективность симплекс метода уменьшается, поскольку начинает сказываться стандартная ошибка измерений.
Лекция 14 Имитационное моделирование Общие понятия. Технические объекты и процессы, изучаемые в металлургии, сложны и часто не поддаются исследованию обычными теоретическими методами. Натурный эксперимент над ними долог, дорог, опасен, либо невозможен, если система является недоступной для исследователя. Поэтому применение как гносеологического так и кибернетического подходов затруднено. Имитационное – воспроизведение на ЭВМ (имитация) процесса функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени. Имитационное моделирование заключается в конструировании мысленной модели, имитирующей объекты и процессы по нужным показателям. Например, по времени работы, интенсивности, экономическим затратам, расположению в цехе. Именно неполнота описания объекта делает имитационную модель принципиально отличной от математической в традиционном смысле этого слова. Данное направление моделирования позволяет осуществить перебор в диалоге с ЭВМ огромного числа возможных вариантов и выбрать наиболее приемлемые с точки зрения инженера решения. При этом используется интуиция и опыт инженера, принимающего решение, понимающего всю сложнейшую ситуацию на производстве. При исследовании таких сложных объектов оптимального решения в строго математическом вообще можно не найти. Зато можно получить приемлемое решение в сравнительно короткие сроки. Имитационная модель включает в себя эвристические элементы, использует иногда неточную и противоречивую информацию. Этим имитационное моделирование ближе к реальной жизни и более доступно для пользователей-инженеров в промышленности. В диалоге с ЭВМ специалисты расширяют свой опыт, развивают интуицию и, в свою очередь, передают их имитационной модели. Обычно имитационное моделирование используется в случае, когда нужно провести достаточно большое число «машинных опытов», чтобы получить достоверный результат. Другими методами такую задачу решить практически невозможно, или не целесообразно из-за больших экономических затрат. В принципе имитационное моделирование можно осуществлять на широком спектре устройств, начиная с аналоговых ЭВМ и кончая листом бумаги с карандашом, однако, как правило, ориентируются на использование ЭВМ. Во многих случаях говорят о «вычислительном эксперименте». В литературе метод имитационного моделирования встречается также под названиями метода цифрового, машинного, статистического, вероятностного, Монте-Карло, динамического моделирования или метода машинной имитации. Метод имитационного моделирования может рассматриваться как своеобразный экспериментальный метод. Отличие от обычного эксперимента заключается в том, что в качестве объекта экспериментирования выступает имитационная модель, реализованная в виде программы на ЭВМ. При таком экспериментировании с моделью (в отличие от «решения» модели при аналитическом, например, моделировании) могут быть применены статистические методы, в том числе метод планирования эксперимента. С помощью имитационной модели невозможно получить аналитические зависимости между величинами, но можно определенным образом обработать экспериментальные данные и подобрать соответствующие математические выражения. При создании имитационных моделей в настоящее время используются два подхода: дискретный и непрерывный. Выбор подхода в значительной степени определяется свойствами объекта-оригинала и характером воздействия на него внешней среды. Однако, непрерывный процесс изменения состояний объекта очень часто можно рассматривать как последовательность дискретных состояний и наоборот. Методы исследования объектов, основанные на построении их дискретных вероятностных имитационных моделей и на целенаправленном экспериментировании с этими моделями, получил название метода статистического моделирования. (Возможна путаница в терминологии, когда «чисто» экспериментальные вероятностные модели также называют статистическими). В этом смысле метод статистического моделирования можно рассматривать как частный случай дискретных вероятностных имитационных моделей. Этот метод называют также методом Монте-Карло или методом статистических испытаний. (Однако эти же названия методов используются и для обозначения численных методов решения чисто аналитических задач – вычисления многомерных интегралов и т. п.: это опять же приводит к терминологической путанице.) При использовании дискретного подхода к созданию имитационных моделей обычно применяются абстрактные системы математические схемы трех основных типов: автоматные системы, системы массового обслуживания и агрегативные системы. В качестве имитационной модели объекта обычно выступает программа на ЭВМ (вместе с обслуживающими, сервисными программами), написанная либо на универсальных языках высокого уровня, либо с применением специализированных языков имитационного моделирования. Еще раз заметим то обстоятельство, что при разработке любых типов моделей успех в значительной степени зависит от изобретательности, интуиции и находчивости исследователя, а также от его знаний и умений. Имитационное моделирование наиболее эффективно использовать на высоких уровнях иерархии (метауровень) при рассмотрении взаимодействия во времени большого числа сложных объектов, что характерно для высших ступеней технологии и производственных процессов. При этом «элементарными» моделями, входящими в состав имитационной модели, могут быть любые математические схемы: от дифференциальных и алгебраических уравнений до систем массового обслуживания и так называемых агрегативных систем, включая модели, полученные экспериментальными методами.
Пример разработки имитационной модели. Рассмотрим конкретный пример разработки имитационной модели описанный академиком Полухиным в книге “Зачем металлургу математические модели?”. В данном примере рассматривается работа мостового крана одного из цехов медеплавильного завода. Следует отметить, что в данном случае речь идет не о самом технологическом процессе производства меди, а об элементе производственного процесса. В литейном цехе медеплавильного завода имеются такие компоненты, как плавильные печи, разливочные пролеты, установки для полунепрерывной разливки под давлением. Продукцией цеха являются пассивные заготовки, направляемые далее на прокатные станы или штамповочные пресса. Плавильные печи работают с использованием различных комбинаций шихты и лома цветных металлов. На разливочном участке работает кран типа портального. Весь цех обслуживается мостовым краном, работа которого подвергается анализу в связи с возможным расширением производства. От нагрузки на мостовой кран в большой степени зависят показатели работы цеха. Некоторые виды задержек возникают из-за наложений заданий. В связи с этим был поставлен следующий вопрос: какая часть мощности литейного оборудования будет потеряна в результате расширения производства, если оставить существующую систему управления краном? Для того, чтобы ответить на этот главный вопрос, нужно было найти ответы на такие вопросы: какова будет степень наложения заданий для крана? как увеличится загрузка крана? соответствует ли увеличение наложения заданий затратам на исследования по его снижению? существует ли здесь вообще серьезная проблема? Инициатором проведения исследования стала администрация предприятия, что существенно упростило проведение работ. С помощью администрации и линейных руководителей (мастеров, бригадиров) было установлено, что мостовой кран выполняет 16 типов различных заданий, каждое из которых подразделялось (детализировалось) на подзадания. Например, одно задание могло состоять из пяти подзаданий с указанием времени выполнения каждого из них. Такое детальное описание заданий позволило обоснованно присвоить каждому из них определенный приоритет по необходимости выполнения. Информация была получена на основе бесед, а также в результате изучения журналов технологического процесса и эксплуатации оборудования за несколько месяцев. Целью этого этапа было получение частот появления событий по заданиям. Затем были установлены (идентифицированы) все задания для крана, получены распределения частот событий по заданиям каждого типа, стал известен характер распределения событий и всем событиям были приписаны приоритеты (табл. ХХ). Как отмечалось, каждое крановое задание по узловым точкам (границам операций) подразделяется на подзадания, и в узловых точках любая операция может быть прервана в том случае, если поступает заявка на задание с более высоким приоритетом. Для построения имитационной модели кроме имеющейся информации нужно знать и логические связи между операциями. В нашем случае необходимо знать логику последовательности операций (шагов), которые выполняет кран. При этом должен быть известным и тот факт, какие события могут произойти одновременно и какие события должны произойти в разное время. С помощью руководителей производства была составлена матрица, фиксирующая события, которые не могут произойти одновременно. Анализ таблицы показывает, что, во-первых, не могут произойти одновременно события, расположенные на диагонали матрицы (+), так как это – те же самые события. Во-вторых, например, случайные задания могут быть всегда, поэтому в этой строке стоит только один символ на диагонали. В-третьих, если, например, идет плавка (непредвиденные замены по ходу плавки), то невозможно загружать плавильную печь и т. д. Логика программ, используемых при моделировании, должна также предусматривать разработку алгоритмов генерации (образования) заявок на выполнение заданий в соответствии с заданными законами распределения. Выяснилось, что задания мостовому крану могут выдаваться по заявкам трех типов: · равномерно распределенные случайные события во времени, т. е. поступление заявки равновероятно в любой момент времени; · случайные события с некоторым известным, но меняющимся циклом; · фиксированные (относительно) во времени события. Моделирующая программа была разбита на три модуля, соответствующих трем типам событий. Например, замена отливочных форм представляет собой пример фиксированного события, а случайные задания - «число» случайной величины, равномерно распределенной во времени. Конечно, следует иметь в виду, что здесь также вводятся определенные допущения для упрощения задачи. Как отмечалось, каждое из 16 заданий разбивалось с помощью узловых точек на подзадания. В любой узловой точке задание могло быть прервано в случае, если поступала заявка на новое задание с более высоким приоритетом. Выполнение отложенного задания или нескольких заданий должно быть завершено, как только позволит их приоритет и загрузка крана. Таким образом, модель описывала управление мостовым краном очень близко к тому, что было на самом деле, т. е. осуществлялась комбинация логической последовательности появления событий (согласно технологическому процессу в цехе) и последовательности случайных событий (отказы оборудования, случайные задания и т. п.). Фиксированные задания обрабатывались следующим образом: «ежедневно» имитировалась функция формирования кодов фиксированных заданий, подлежащих выполнению в течение «дня». Такая имитация в сочетании с различными операторами формирования подчеркивала определенную логическую последовательность поступления заданий для крана в течение всего периода работы модели. Наименьшая единица времени, используемая в модели, составляла 1 мин; полный период моделирования был равен 1 мес. Прогон имитационной программы, моделирующей работу крана в течение 1 мес, занимал 25 мин. Необходимый объем оперативной памяти составил 220 Кбайт. Результаты, полученные с помощью модели, хорошо совпали с реальными данными производства. Модель показала, что кран справляется со всеми заданиями, которые предназначены для него в течение месяца, и дала возможность учитывать расширение производства. Сравнение результатов моделирования существующего литейного производства, близко совпавших с реальными данными, и результатов расширенного производства с дополнительным оборудованием позволило сделать ряд заключений. Основной вывод состоял в том, что из-за возрастающего наложения заданий общая производственная мощность могла снизиться на 2,8%. Задача получила количественное решение, и далее руководству следовало определить нужные действия. Таблица Лекция 15 Геометрическое моделирование Геометрическая модель - математическое представление геометрической формы, хранимое в памяти компьютера. Различают двухмерные (2D-модели) и трехмерные (3D-модели) модели. Аналогично подразделяются и системы, обеспечивающие плоское и объемное проектирование. Как правило, современные 3D-системы проектирования имеют встроенные 2D-системы, необходимые для изготовления плоских чертежей. Элементы, из которых состоит трехмерная модель, образуют в ней вершины, ребра, грани рис. 1.
Рис. 1 – Элементы трехмерной модели: 1 – вершины; 2 – грани; 3 – поверхности; 4 – базовая плоскость; 5 – начало координат. Вершина – точка являющаяся окончанием (началом) ребра. Ребро – прямая или кривая, разделяющая две смежные грани модели. Грань – гладкая часть поверхности модели. Гладкая поверхность модели может состоять из нескольких граней. Методы трехмерного моделирования, предоставляемые системами САПР, делятся на три категории: каркасное, поверхностное (полигональное) и твердотельное (сплошное) моделирование. Каркасное моделирование Процесс каркасного моделирования представляет собой моделирование самого низкого уровня. Каркасная геометрическая модель полностью описывается с помощью линий и точек. Существенным недостатком каркасного моделирования является недостаток информации о внешней и внутренней поверхности объемного тела. Однако каркасная модель требует гораздо меньше компьютерной памяти, чем остальные модели, и пригодна для решения простых задач. Каркасное моделирование широко используется для имитации траектории движения инструмента, выполняющего несложные операции обработки детали, такие, как фрезерование по двум с половиной или трем осям. Ограничения каркасных моделей 1. Неоднозначность. Одним из основных недостатков рассматриваемых моделей является сложность интерпретации ориентации видимого изображения. Например, на рис. 2, трехмерное изображение (рис. 2а) можно интерпретировать и как вид сверху (рис. 2б), и как вид снизу (рис. 2в). Этот эффект, обусловленный природой каркасной модели, сильно усложняет работу конструктора. В отличие от твердотельной модели в каркасной модели нельзя отличить "видимые" грани геометрической формы от "скрытых" (невидимых).
Рис. 2 – Неоднозначность каркасной модели.
2. Невозможность распознавания криволинейных поверхностей. Боковые поверхности цилиндрических форм не имеют ребер, хотя на изображении видно силуэты мнимых ребер, которые ограничивают поверхности. Расположение этих "ребер" в пространстве меняется в зависимости от направления вида (точки зрения), поэтому такие силуэты не являются элементами каркасной модели. На рис. 3 показано трехмерное изображение твердотельной и каркасной моделей. Видимые на рис. 3а мнимые “ребра” отсутствуют на главном виде (рис. 3б) и на видах сверху (рис. 3в) и справа (рис. 3г)
Мнимые “ребра”
Рис. 3 – Мнимые ребра каркасной модели.
3. Невозможность обнаружения взаимного влияния компонентов. Поскольку каркасная модель не несет информацию о поверхностях, ограничивающих форму, то при использовании такой модели нет возможности обнаружить нежелательные взаимодействия между поверхностями объекта. Это существенно ограничивает применение каркасного моделирования при трехмерном кинематическом анализе механизмов, имитации функционирования роботов, проектировании планов размещения заводского оборудования и выполнении сложных сборочных чертежей. Ограничено использование каркасных моделей и в пакетах, имитирующих траекторию инструмента, потому что при таком моделировании не могут быть выявлены на стадии проектирования ошибки, возникающие при механической обработке. 4. Трудности вычисления физических характеристик. Поскольку правильно построенная геометрическая форма, (объем тела), отличается от стандартных базовых компонентов, то физические характеристики могут быть определены неточно. Таким образом, значения физических характеристик (например, масса, площадь поверхности, центр тяжести или моменты инерции) будут недостоверными. Поверхностное моделирование Поверхностная модель в отличие от каркасной дополнительно определяется с помощью поверхностей. Таким образом, ее можно рассматривать как модель более высокого уровня, чем каркасная, а, следовательно, как более гибкую и многофункциональную. Поверхностное моделирование имеет следующие преимущества по сравнению с каркасным: 1. способность распознавать и изображать сложные криволинейные поверхности, 2. способность распознавать грани и таким образом обеспечивать средство получения тоновых трехмерных изображений; 3. способность распознавать особые построения на поверхностях, например, отверстия; 4. возможность получения более качественного, чем при каркасном моделировании изображения; 5. обеспечение удобного производственного интерфейса со станками с ЧПУ при имитации траектории движения инструмента в трехмерном пространстве; Основные виды поверхностей, используемые при моделировании. Применительно к поверхосному моделированию можно выделить следующие типы поверхностей: 1. Базовые геометрические поверхности. Это плоские поверхности, которые можно получить, движением заранее построенного отрезка прямой в указанном направлении на заданную величину (рис. 4а). Заменив отрезок прямой на дугу можно получить цилиндрическую поверхность (рис. 4б).
Рис. 4 – Построение базовых геометрических поверхностей.
Отличительной особенностью систем поверхностного моделирования является то, что они не распознают такие построения, как твердые объемные тела; они представляют их просто как поверхности, соединенные друг с другом неким образом в пространстве и ограничивающие "пустой" объем. На рис. 5 показана геометрическая модель, построенная в системе поверхностного моделирования за счет развертки исходного контура. Несмотря на то, что, на экране модель представлена виде объемного тела, в компьютерном представлении модель состоит из пяти поверхностей.
Рис. 5 – Визуальное и компьютерное представление поверхностной модели.
2. Поверхности вращения могут быть получены по команде, создающей поверхность вращением плоского контура вокруг определенной оси. При этом опять необходимо помнить, что создается не объемное тело, а генерируется только поверхность (рисунок 7).
Рисунок 7 – Создание поверхности вращения.
3. Поверхности сопряжений и пересечений. Такие поверхности получаются при создании плавных переходов в местах соединения двух различных по форме элементов. Возможность построения Плавного сопряжения одной поверхности с другой является наиболее мощными часто используемым на практике средством поверхностного моделирования. На рис. 7 показаны поверхности сопряжения (внешняя и внутренняя) построенная на пересечении двух элементов детали (поверхность сопряжения - радиусный участок детали в переходе от основного участка трубы к ответвлению).
Рис. 7– Поверхности сопряжения.
4. Аналитические поверхности. Каждая такая поверхность определяется одним математическим уравнением с неизвестными X, Y, Z (эти неизвестные обозначают искомые координаты поверхности в координатном пространстве). Для изображения аналитической поверхности, необходимо знать математическое уравнение, которым оно описывается. 5. Скульптурные поверхности (поверхности "свободных форм" или "произвольные" поверхности) нельзя описать одним математическим уравнением. В большинстве случаев образы этих поверхностей создаются путем построения кривых продольных образующих между точками, определенными в трехмерном пространстве (рис. 8).
Рис. 8 – Скульптурные поверхности.
Несмотря на то, что методы поверхностного моделирования обладают многими достоинствами существует ряд ограничений на их использование. К подобным ограничениям можно отнести: а) возникновение неоднозначности при попытке моделирования реального твердого тела; б) недостаточная точность представления некоторых поверхностных моделей для обеспечения надежных данных о трехмерных объемных телах; в) сложность процедур удаления скрытых линий и отображения внутренних областей. Твердотельное моделирование Твердотельная модель описывается в терминах того трехмерного объема, который занимает определяемое ею тело. Твердотельное моделирование является единственным средством обеспечивающим полное однозначное описание трехмерной геометрической формы. Достоинством твердотельных моделей являются: 1. полное определение объемной формы с возможностью разграничения внешней и внутренней областей объекта, что позволяет обнаружить нежелательные взаимовлияния компонентов; 2. обеспечение автоматического удаления скрытых линий; 3. автоматическое построение трехмерных разрезов компонентов, что особенно важно при анализе сложных деталей и сборочных изделий; 4. получение точных весовых характеристик детали; 5. возможность получения наиболее качественных цветовых и тоновых изображений; 6. повышение эффективности имитации процедур генерации траектории движения инструмента. Наиболее часто применяемые методы твердотельного моделирования можно разделить на два класса: метод конструктивного представления (метод C-Rep) и метод граничного представления (метод B-Rep). Они отличаются друг от друга способом хранения моделей в памяти компьютера. Моделирование методом конструктивного представления (C-Rep) заключается в построении твердотельных моделей из базовых элементов, называемых твердотельными примитивами и определяемых формой, размерами, точкой привязки и ориентацией. Инструментом для построения модели C-Rep при определении взаимоотношений между соседними примитивами являются булевы операции, которые базируются на алгебраической теории множеств. В качестве примера рассмотрим три булевы операции: объединение, разность и пересечение (рис. 9). Операция объединения. Результатом операции является общая составная форма представляющая один элемент. Объединение двух произвольных фигур показано на рисунке 9б (заштрихованная область). Операция разности. Результатом выполнения операции является фигура находящаяся внутри границ ограниченных поверхностью, оставшейся от одной формы, и внешней границей общей области двух форм. На рисунке 9в заштрихованной областью показан результат действия операции булевой разности. Операция пересечения. Результатом является фигура находящаяся внутри границ общей области объектов. Пересечение фигур представлено на рис. 9г заштрихованной областью.
Рис. 9 – Результаты булевых операций. Как при поверхностном моделировании твердотельные примитивы могут быть созданы с помощью развертки двухмерных областей в трехмерном пространстве, только в данном случае образуется существенно "твердый объем", а не пустое пространство, ограниченное несколькими поверхностями. Моделирование методом B-Rep (граничного представления) похоже на C-Rep моделирование. Вначале строятся примитивы с помощью линейной или круговой развертки, а затем с помощью булевых операций выполняется построение из них составных форм. Различие между методами граничного и конструктивного представления состоит в том что пакеты моделирования C-Rep распознают сложную форму в терминах составляющих ее твердотельных примитивов, тогда как пакеты анализа B-Rep оперируют с моделью в терминах ребер и граней, которые образуют трехмерную граничную поверхность объемного тела. Достоинством моделирования методом B-Rep является возможность более легкой модификации граничной поверхности. Однако соответствующие системы моделирования методом граничного представления требуют большего объема компьютерной памяти. Различия между рассматриваемыми типами твердотельного моделирования невелики, и в некоторых системах применяется комбинация этих двух методов. Помимо построения моделей с помощью булевых операций можно решить и ряд других задач. 1. Вычисление объемных и весовых характеристик. Булевы операции сложения и разности используются для построения составной твердотельной модели. После каждого преобразования модели автоматически рассчитывается объем и сразу же корректируются ее весовые характеристики. 2. Расчет напряжений. Применяя булевы операции разности так же, как они использовались для получения разрезов, можно разбить трехмерную модель на твердотельные конечные элементы для проведения расчета напряжений. 3. Имитация операций механической обработки является одним из наиболее важных применений булевых операции при твердотельном моделировании. Используя особенности твердотельного моделирования можно смоделировать такие операции как точение, фрезерование и сверление.
Рисунок 11 – Процесс Механической обработки.
В качестве примера можно привести рис. 10, где производиться сопоставление процесса получения фрезой шпоночной канавки. Процесс моделирования может быть осуществлен следующим образом сначала фреза (рис. 10б) и брусок (рис. 10а) размещаются в необходимом положении (рис. 10в) в соответствии с требуемой глубиной канавки. Затем задаются длина канавки и скорость подачи фрезы, наконец, выбором из меню соответствующей команды запускается собственно процесс имитации фрезерования. После всех этих манипуляций система уже сама определяет пересечения фрезы с бруском и управляет модификацией изображения «изготавливаемой» детали. Этот процесс программно реализован через цикл, на каждом шаге которого происходит постепенное увеличение булевой разности между бруском и фрезой. Данный цикл завершает работу при достижении требуемой глубины канавки (соответствующего значения булева пересечения). При необходимости изображение этого пересечения – (результата фрезерования) и значение его объема (количества, отходов при фрезеровании) можно вывести на дисплей (рисунок 9г,д). 4. Обнаружение взаимовлияния и пересечений позволяет проверять наличие пересечений между примыкающими друг к другу объектами и оповещать о существовании пересечений, если они имеют место. Средства такой проверки являются необходимым инструментарием для обработки ошибок появляющихся при конвертации геометрической модели. Эти же средства могут применяться для выявления ошибок при движении резца относительно обрабатываемой деталью при имитации механических операций, а также для обнаружения препятствий при размещении сложных механизмов. Понятие гибридного моделирования Возможность свободного создания и изменения различных объектов вне зависимости от того, каким образом в математическом представлении описывается объект (с помощью каркасного, поверхностного или сплошного моделирования) является сильной стороной любой системы моделирования. Подобное сочетание возможностей различных методов появляется с использованием технологии гибридного моделирования. При построении в подобных системах право выбора эффективной стратегии (т.е. вид представления модели) каждого элемента одного и того же объекта принадлежит пользователю. Обычно построение модели с помощью систем гибридного моделирования осуществляется на основе твердотельных объектов, а затем добавления элементов построенных с помощью поверхностного моделирования (например, таким объектом могут быть скульптурные поверхности). На следующем этапе данные поверхностные элементы превращаются (часто автоматически) в твердые тела и далее к ним могут быть применены все операции характерные для работы с твердыми телами.
Лекция 16 Современные программные средства конечно-элементного анализа Развитие метода конечных элементов обусловлено взаимосвязью трех факторов: наличием высокопроизводительной вычислительной техники; разработкой математических моделей исследуемых явлений, адекватных реальным процессам с достаточной степенью точности; особенностями самого метода [26]. Первые программные комплексы, в которых реализован метод конечных элементов, были разработаны в 60-х годах. К ним относятся STRUDL-II, SAP-IV, NONSAP, ASKA, NASTRAN, SESAM-69 и другие [41]. Появлению этих универсальных программных систем в силу особенностей метода конечных элементов предшествовало создание высокопроизводительных электронно-вычислительных машин, таких, например, как IBM-370. Начиная с конца 70-х годов в СССР появилось несколько десятков программных комплексов для разных ЭВМ, в которых был реализован МКЭ. К их числу относятся МИРАЖ [13], МОРЕ [27], КАСКАД-2 [28], ПРОЧНОСТЬ-75 [17], МКЭ/20 [10], МАРС [11], ПАРСЕК [7], ЛИРА [14], СПРИНТ [34], FEA [4] и ряд других программ [33]. В США и ряде других стран дальнейшее развитие МКЭ и необходимость в проведении расчетов конструкций на прочность также способствовали дальнейшему развитию уже созданных программных комплексов и разработке новых. Были разработаны сотни программных комплексов, предназначенных для приближенного решения самых разнообразных задач не только из области механики деформируемого твердого тела, но и из таких областей как гидродинамика, акустика, электротехника и т.д. Наибольшее распространение из них получили [40]: ABAQUS, ADINA, ASKA/DYNAN, ANSYS [2], MARC, MSC/NASTRAN [35], EUFEMI, COSMOS, HERCULE, MODULEF, SAP-7, LS-DYNA. Отметим, что разработка программных комплексов является дорогостоящим делом. Поэтому, как правило, организации и фирмы – собственники разработанных программ, рассматривают их как коммерческий научно-технический продукт. Регулярно печатаемые обзоры существующих комплексов программ и их характеристик, сведения о программах в отраслевых фондах алгоритмов и программ позволяют пользователям программной продукции целенаправленно выбирать необходимые для их деятельности программы расчета. У каждой программы есть свои сильные и слабые стороны при расчете конкретной конструкции. Выбор программы расчета зависит от подготовленности пользователя в своей научной области, типа решаемой задачи, типа доступной ЭВМ, размерности задачи и других факторов. К критериям, помогающим сделать выбор, следует отнести следующие факторы: · программа широко используется; · в программе используются новейшие научные достижения; · программа коммерчески вполне доступна; · имеется подробная и понятная документация. Ознакомление с программной документацией и доступной литературой с описанием программы и ее элементов позволяют сделать окончательный вывод о целесообразности выбора программного комплекса. Для МКЭ характерны особенности, которые следует учитывать при выборе и разработке программы расчета. Такими особенностями являются большие объемы исходных данных, промежуточных и окончательных результатов расчета. Поэтому расчет по МКЭ состоит из трех основных этапов: · разработка расчетной конечно-элементной схемы и подготовка исходных данных; · проверка самого расчета; · обработка результатов расчета. На рис. 17.1. приводится одна из возможных схем организации расчета по МКЭ [33]. Каждый этап является самостоятельной задачей. На первом этапе самое существенное заключается в создании начальной конечно-элементной расчетной модели, исходя из инженерной интуиции о поведении конструкции. В последствии эта модель может корректироваться на основе анализа результатов расчета. Корректировка модели может выполняться и программным путем, если такая возможность реализована в используемом программном комплексе. Подготовка исходных данных осуществляется, как правило, с помощью программ генераторов сеток конечных элементов, образующих блок подготовки данных.
Рис. 17.1. Схема организации расчета по МКЭ.
Проведение расчета (этап 2) осуществляется расчетным блоком, в котором используется тот или иной алгоритм расчета методом конечных элементов. Как правило, расчетный блок состоит из ряда программных модулей, каждый из которых выполняется на определенном шаге алгоритма. В простейшем случае программной реализации МКЭ для линейной статической краевой задачи теории упругости расчетный блок содержит следующую последовательность шагов: · ввод исходных данных (например, подготовленных программой-генератором в отдельном файле); · вычисление матриц жесткостей конечных элементов; · формирование глобальной матрицы жесткости полной структуры; · формирование глобального вектора нагрузок; · решение системы линейных алгебраических уравнений; · вычисление перемещений узлов сетки конечных элементов, деформаций и напряжений в произвольных точках конечных элементах. На различных шагах расчетного блока включаются проверки правильности исходных данных и результатов промежуточных вычислений (диагностика ошибок), программные модули выбора сочетаний нагрузок, действующих на конструкцию, определение площади сечений арматуры в железобетонных конструкциях и другие. Диагностика ошибок на этапе выполнения программы является важной, так как при своевременном обнаружении ошибки прекращаются вычисления, что приводит к экономному использованию ресурсов ЭВМ. Эффективное использование ЭВМ достигается также за счет разработки специальных методов решения стандартных математических задач, учитывающих специфику МКЭ, и, в первую очередь, ленточность и разреженность матрицы жесткости расчетной модели конструкции. Расчет напряженно-деформированного состояния конструкции в рамках линейной теории упругости при действии на нее статических нагрузок сводится к решению системы линейных алгебраических уравнений. В конечно-элементных комплексах программ используются разнообразные методы решения больших систем уравнений. Различные варианты метода Гаусса реализованы в программах ADINA (блочный метод Гаусса), ASKS, SAP-7 (ленточный метод Гаусса), NASTRAN (LTDL - декомпозиция). Эффективным является фронтальный метод, реализованный в программах ABAQUS, ANSYS и др. Методы суперэлементов и редукции базиса позволяют существенно сократить время вычисления [18]. Эффективными являются также итерационные методы [1]. Расчет собственных колебаний конструкции выполняется методами: итерации в подпространстве (SAP-7), вычисления корней характеристического определителя (NASTRAN), Хаусхолдера с использованием метода Якоби (ASKA), Гивенса и QR-метода (NASTRAN), Hiber-Hughes (ABAQUS), Ланцоша (PKM). При расчет динамического отклика используются методы: представления решения в виде суперпозиции форм собственных колебаний, шаговые – Вилсона, Ньюмарка (ABAQUS, ADINA, SAP-7, NASTRAN). Решение геометрически и физически нелинейных задач осуществляется, как правило, итерационными методами, основу которых составляет метод Ньютона-Рафсона в сочетании с шаговыми методами (ABAQUS, ADINA, NASTRAN, ANSYS, LASTRAN и др.) [33]. Следует отметить, что принцип модульности программирования, использованный в программных комплексах, позволяет создавать как универсальные вычислительные программы, так и промышленные для решения узкого класса задач. На первых этапах освоения МКЭ разрабатывались в основном промышленные вычислительные программы. Они эффективны, если решается большое количество вариантов однотипных задач, либо выполняется большой объем вычислений для качественного и количественного исследования явлений, связанных с новой постановкой задачи. Тенденция развития вычислительной техники, приведшая к созданию персональных ЭВМ и новых информационных технологий, оказала влияние на разработку программного обеспечения МКЭ [6]. Программные комплексы по МКЭ активно используются в системах автоматизированного проектирования, базирующихся на персональных ЭВМ (AutoCAD/MechanicalDesktop, Pro-Engineer). Краткие характеристики некоторых программных комплексов Современные комплексы программ, в которых используется МКЭ, позволяют получать приближенные численные решения при расчете конструкций на статические и динамические нагрузки для широкого класса материалов с различными механическими характеристиками и поведением. Расчет конструкций на статические нагрузки может производиться с учетом физической и геометрической нелинейности, температурных полей, взаимодействия с другими средами (например, с жидкостью). Производится расчет критических нагрузок, при которых конструкция или ее элементы теряют устойчивость, поведения конструкции после потери устойчивости. МКЭ позволяет также определить нагрузки, при которых происходит разрушение конструкции. Учитываются такие свойства материала как анизотропность, нелинейная упругость, пластичность, текучесть. Учитываются виды геометрической нелинейности: большие деформации и большие перемещения. Основными динамическими задачами являются: расчет собственных колебаний конструкции; динамический отклик на нагрузку, зависящую от времени; распространение волн [33]. Ниже в таблице 17.1. приводятся сравнительные характеристики наиболее распространенных комплексов программ описанных в работе [40].
Таблица 17.1. Краткие характеристики наиболее распространенных комплексов программ МКЭ
Приведенные в таблице комплексы программ являются универсальными. Опишем подробно один из комплексов, например, ABAQUS [33]. Этот программный комплекс разработан относительно недавно для расчета новых прогрессивных конструкций. Разработчики этого комплекса (Hibbit, Karlson, Sorensen) сохранили простоту и эффективность расчета для линейных задач при учете сугубо нелинейных эффектов – геометрических и физических. Комплекс программ позволяет производить расчет стационарных и нестационарных температурных полей, их влияния на напряженно-деформированное состояние конструкции, ее устойчивость, оценивать трещинообразование, учитывать зоны контакта с
|



 X2
X2
 X1
X1


 X X
X X



 а)
а)  б)
б)  в)
в) а)
а) 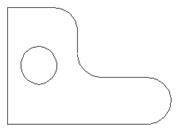 б)
б)  в)
в)  г)
г) а)
а)  б)
б)




 а)
а)  б)
б)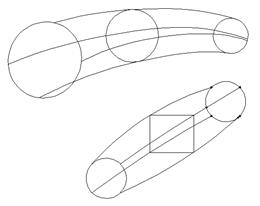
 плоское
плоское




 объемное
а)
объемное
а)
 б)
б)
 в)
в)
 г)
г)