Часть II – Методы построения моделей.
Добавить лекцию по технологиям быстрого прототипирования. Лекция 6 Теоретические методы решения задач ОМ. Основные допущения. Использование гносеологического подхода позволяет получать математическое описание объекта, основываясь на математическом анализе физических, химических и др. явлений протекающих в исследуемом объекте. Сложный характер подобных явлений, возникающих при обработке металлов, требует построения сложных и точных математических моделей. Поэтому степень совершенства используемых для расчета аналитических моделей характеризует в целом развитее наук связанных с обработкой металлов. В соответствии с данным подходом появляется возможность получать модели требуемой точности зависимой лишь от степени достоверности принятых допущений. Существенным недостатком аналитических моделей, как правило, является сложный характер участвующих при построении модели параметров, что создает определенные сложности при дальнейшем использовании полученной аналитической модели. Например, при исследовании данной модели при поиске оптимального значения исследуемых параметров, или при использовании модели для автоматического управления технологическим процессом. Данный недостаток может быть устранен за счет аппроксимации аналитически полученной зависимости более простыми и удобными для использования зависимостями, которые и могут быть использованы для дальнейшего управления технологическим процессом или поиска оптимального значения. В этом случае точность используемой модели будет ниже, но сама модель будет более удобной для исследования или управления технологическим процессом. Задачи металлургии, решаемые наиболее часто с помощью моделирования можно разделить на 3 группы: 1. Задачи теплообмена – решая эти задачи, осуществляется подбор различных режимов термообработки для различных по форме деталей из различных материалов, учитывать влияние термических напряжений на форму и свойства детали после предлагаемой ТО. Программы Ansys, Deform, Super Forge. 2. Задачи, описывающие гидродинамическое течение металла при литье. Позволяют описать процессы заполнения литейной оснастки, оценить качество предложенной детали, оценить размеры усадки. Программа Полигон. 3 Задачи описания процессов протекающих в металле при его деформации. Позволяют осуществлять расчет технологических параметров процессов ОМД, оценит качество возможного изделия, и оценить стойкость оснастки. Рассмотрим первую группу задач. Как правило, задачи этой группы являются наиболее простыми с точки зрения моделирования, поскольку рассчитывают перенос тепла в твердом теле теплопроводностью. Напомним, что в общем случае перенос тепла может осуществляться тремя способами: теплопроводностью, конвективным теплообменом и лучистым теплообменом. В случае теплопроводности перенос тепла осуществляется между твердыми соприкасающимися частицами. Поэтому используемая в моделировании теория теплопроводности рассматривает исследуемое тело как непрерывную среду – континуум. В этом случае не учитывается реальное молекулярное или атомное взаимодействие частиц реального тела. На самом деле как процессы, протекающие внутри тела, так и процессы, связанные с взаимодействием тел объясняются именно взаимодействием частиц на атомном и молекулярном уровнях. Второе допущение связано с тем, что свойства тела во всех направлениях являются однородными. При моделировании задач теплопроводности могут использоваться изотропные и ортотропные модели. В изотропной модели свойства теплопроводности одинаковы во всех направлениях по всему телу, в то время как в ортотропной модели свойства одинаковы по всему телу, но различны в зависимости от направления.
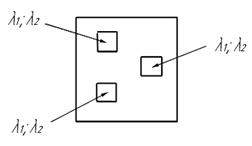
Рис. 9 – Иллюстрация к допущению однородности тела: а – однородное тело; б – изотропное тело; в – ортотропное. Если выделить в теле элемент сплошной среды и считать что оси координат совпадают с главными направлениями теплопроводности, то количество теплоты проходящее через изотермическую площадку в единицу времени определяется величиной коэффициента теплопроводности в указанном направлении.(см. теор. теплообмена).
Рис. 10 – Иллюстрация к описанию задачи теплопроводности. Очень часто задачи теплообмена решаются с другими задачами металлургии. Например, с задачами пластического деформирования металла или насыщением поверхностного слоя металла специальными химическими компонентами, что реализуется, например, в программе Deform. Рассмотрим третью группу задач. Задачи механики твердого тела являются наиболее сложными задачами анализа. В данной группе задач помимо допущения о сплошности тела и однородности его свойств используется также допущение (гипотеза) о не сжимаемости тела. Согласно данному допущению осуществляется пренебрежение упругим сжатием тела. Наиболее распространена запись этой гипотезы в виде условия постоянства объема, по которому деформация тела в трех взаимно перпендикулярных направлениях равна нулю. Из курса сопромата известно, что детали меняют форму под действием внешних сил. Действие внешних сил вызывает в теле внутренние усилия, значение и распределение которых зависит от геометрии тела и характера приложения нагрузки.
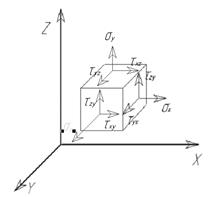
Рис. 11 – Напряженное состояние тела в точке и тензор напряжений. В соответствии с теорией напряженное состояние тела в точке характеризуется с помощью тензора напряжений. Под тензором напряжений понимается совокупность в общем случае девяти напряжений действующих на бесконечно малых площадках вокруг рассматриваемой точки. Если рассматривать элементарный прямоугольный параллепипед находящийся в равновесии под действием внутренних сил, то его длина по отношению к моменту тогда усилие не было приложено, изменится. Это явление называется деформированием, а мера изменения размера – деформацией. Аналогично тензору напряжений деформированное состояние тела принято описывать с помощью тензора деформаций содержащего шесть компонентов деформаций в разных направлениях Для решения задач механики твердого тела. (Например, для того чтобы определить какую форму примет тело при заданной нагрузке) необходимо знать связь между деформациями и напряжениями описывающую особенность поведения материала нагружаемого внешними усилиями. При этом надо учесть тот факт, что свойства различных материалов используемых для моделирования процессов металлургии, сильно отличаются друг от друга. Например, хрупкие материалы разрушаются практически сразу после начала простейших деформаций. Пластичные металлы имеют значительный запас области пластичного деформирования до момента нагружения. Поэтому для описания зависимости между напряжениями и деформацией пользуются несколькими моделями, которые можно разделить на две группы: модели, описывающие упругое и пластичное состояние тела. Наиболее широко используемая модель линейного деформирования (Закон Гука). Данная модель, как правило, используется при решении конструкционных прочностных задач. На рис.12 показано стрелками что после снятия нагружения деформация в теле равна нулю.
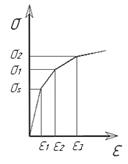
Рис. 12 – Упругие модели среды:а- линейная; б – нелинейная; в – мультилинейная упругая. Другой моделью описывающей поведение нелинейно упругого материала является мультилинейная упругая модель. Данная модель в первом приближении заменяет нелинейную упругую зависимость реальных тел с помощью определенного количества отрезков прямых. Такая модель описывает материалы у которых участок линейного упругого деформирования на диаграмме растяжения очень мал, поэтому практически любая нагрузка, выводит тело за приделы линейного упругого деформирования. Подобная модель может использоваться для описания свойств объектов участвующих в процессе деформирования заготовки. Например, может описывать свойства эластичной среды при штамповке в эластичном контейнере. Модели, учитывающие пластичное состояние тела являются наиболее сложными и наиболее часто применяемые для решения задач ОМД, поскольку пластичные модели описывают поведение материалов деталей в ходе процессов ОМД. Среди моделей описывающих пластическое состояние тела в теории ОМД обычно выделяют следующие:
Рис. 13 – Модели, описывающие пластические свойства материалов: а – идеально пластическая; б – жесткопластическая; в – несжимаемая упрочняемая Идеально пластическая модель – материал на начальной стадии деформируется по закону Гука, по достижению значения придела текучести начинается пластическая деформация материала. Упрочнение не учитывается. Жесткопластическая модель – материал начинает деформироваться по достижению значения напряжения текучести без упругого деформирования на начальном этапе. Упрочнение не учитывается. Напряжение не зависит от деформаций. Данные две модели, используемые для описания тех процессов горячей штамповки, когда процесс упругий разрушающийся при некоторой скорости процесса. Несжимаемая упрочняющаяся модель – упругие деформации отсутствуют пластическая деформация начинается по достижению напряжений значения напряжения текучести которых возрастает в соответствии с условием упрочнения. Упругая пластическая упрочняемая модель – как правило, не используется, поскольку интервал упругих деформаций составляют обычно менее 5 от общей деформации заготовки. Поэтому нет смысла использовать более сложную модель. На практике применение подобных моделей пластических свойств материалов усложняет решение задачи, и поэтому обычно при моделировании на ЭВМ применяются простые и достаточно точные билинейные и мультилинейные модели. Билинейная модель – является апроксеммирующей (заменяющей) кривой растяжения на два отрезка, один из которых описывает упругие свойства модели другой пластичные. Построение модели для конкретного материала осуществляется за счет задания модуля упругости, модуля пластичности и придела текучести материала.
Рис. 14 – Наиболее часто употребляемые модели для описания механических свойств материала: а – билинейная модель; б – мультилинейная. Мультилинейная модель – отличается от билинейной тем, что разбиение диаграммы растяжения осуществляется не на две, а на большее количество отрезков, что позволяет более точно описать поведение реального материала при деформировании. При этом упругий участок по-прежнему описывается одним отрезком.
Рис. 15 – Таблица задания свойств материала программе Deform. Как билинейная, так и мультилинейная модели могут учитывать или не учитывать упрочнение материала в ходе процесса. Обычно для построения мультилиненой модели свойств материала в программах моделирования есть режим задания свойств материалов виде таблицы. Это зачастую наиболее простой режим задания свойств материала основанный на легко доступных экспериментальных данных, в ходе которого осуществляется построение графика модели по точкам, при этом построение зависимости осуществляется для заданной температуры. (Например, при холодной листовой штамповке для при температере 20˚). В случае если при моделировании процесса надо учитывать влияние температуры на свойства материала (например, как в горячей штамповке). То вводится график еще для нескольких температур лежащих в интервале изменения температуры тела по ходу процесса. Следует заметить, что при моделировании процессов ОМД иногда приходит сталкиваться с быстро протекающими во времени процессами (штамповка на ВСМ, и т.д.). В этом случае необходимо, чтобы модель учитывала фактор скорости протекания процесса во времени, поскольку при высоких скоростях обработки свойства материалов отличны от свойств материалов при статичной (медленной) обработке (например, для частей детали). Следует запомнить, что правильный выбор модели, описывающий свойства объекта позволяет значительно сэкономить время расчета на ЭВМ и получить при этом достоверные результаты. Например, при расчете процесса штамповки деталей в открытых штампах пренебрегают деформацией инструмента, считая его абсолютно жестким. В этом случае расчет осуществляется быстрее, поскольку компьютеру приходится рассчитывать деформации только одного тела – заготовки, а не трех как в случае если считать что инструмент (верхний и нижний штампы) деформируются упруго.
Лекция 7 Пример – Модели и ее использования для вытяжки деталей с отверстием Инженерный метод решения.
Вариационные методы решения задач ОМ.
Для определения напряженно деформированного состояния тела достаточно иметь три уравнения равновесия и три уравнения описывающих граничные условия:
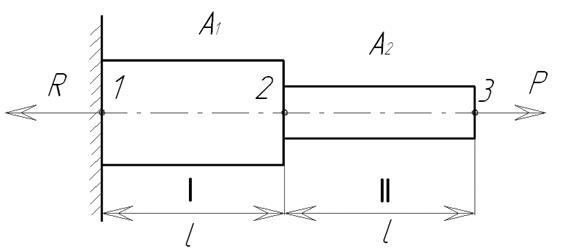
Эта система уравнений является моделью описывающей напряженно деформированное состояние любого тела подвергающегося внешней нагрузке, содержит шесть уравнений с шестью неизвестными, т.е. статически определима. Однако математически решить данную систему для конкретного процесса в большинстве случаев невозможно. Поэтому в ОМ приходиться использовать специальные и упрощенные методы решения систем уравнений. К ним относят: метод решения упрощенных уравнений равновесия и пластичности; метод сопротивления материалов пластическим деформациям; метод характеристик. Суть всех методов одна, и заключается в том, что производиться упрощение существующих физических законов описываемых сложными дифференциальными уравнениями до более простых дифференциальных зависимостей, которые позволяют найти приближенное решение исходной системы /Тарновский/. В ряде случаев задача интегрирования исходной системы дифференциальных уравнений может быть заменена на задачу поиска некоторого значения энергетического функционала. Методы, использующие данный математический подход называются вариационными /Тарновский/. Наиболее широко используемый в настоящее время в программных продуктах метод конечных элементов (МКЭ) то же является варационным. Данный метод является одним из вариантов решения метода Реэля-Рица который путем минимизации потенциальной энергии тела сводит задачу к системе линейных уравнений равновесия. Данный метод нашел применение не только для решения задачи механики сплошных сред, но и для описания многих других физических процессов. Суть МКЭ заключается в том, что непрерывные величины можно заменить на модель, состоящую из отдельных участков (элементов). При этом на каждом из участков исследуемая непрерывная величина заменяется кусочно-непрерывной функцией, построенной на значениях непрерывной исследуемой величины в конечном числе точек. Распределение значений исследуемой величины внутри области и сама непрерывная величина, могут быть неизвестны. При построении дискретной модели мы предполагаем, что численные значения исследуемой величины в конкретных точках (узлах) нам известны. После этого можно перейти к определению значений кусочно-непрерывной функции, за счет подборки значений в узловых точках так чтобы выполнялось условие минимизации потенциальной энергии. Приведем пример: Рассмотрим распределение температуры в стержне. В общем случае распределение температуры внутри стержня неизвестно. Предположим, что значение температуры в некоторых точках в стержне нам известно. Дальше определяют множество узлов, которые являются переменными, поскольку они (значения) являются неизвестными. Длина стержня (область) разбивается на элементы для каждого из которых определяется апроксимирущая функция. Осуществляется расчет узловых значений функции так чтобы с учетом граничных условий (значения температуры по краям стержня) выполнялось наилучшее приближение к выполнению условия минимизации потенциальной энергии температурного функционала. Процесс минимизации этого функционала сводится к решению системы линейных алгебраических уравнений относительно узловых значений температуры. В задачах ОМД минимизируется потенциальная энергия деформируемого тела, а в задачах связанных с теплопроводностью …(см. теор. теплооб. и МКЭ). Таким образом, при построении дискретной модели поступают следующим образом: 1.Область определения исследуемой величины разбивают на КЭ. Эти элементы связаны друг с другом с помощью узлов. Элементы в совокупности аппроксимируют форму исследуемого тела. 2.Считается, что значение исследуемой непрерывной величины в каждом узле известно. Хотя на самом деле эти значения еще предстоит определить в зависимости от поставленных граничных условий. 3.Подбирая значения непрерывной исследуемой величины в узловых точках, определяют ее значения внутри рассматриваемой области (тела). Аппроксимирующие функции подбираются таким образом, чтобы сохранить непрерывность исследуемой величины вдоль границ элемента. В виде апроксимирующей функции могут выступать линейные, и квадратичные и кубические полиномы, которые для данного элемента называются функцией элемента. Поскольку при решении задач металлургии приходится иметь дело с сплошными телами, но основная трудность связана с правильным разбиением сплошного тела на дискретные (модельные) элементы взаимодействующие друг с другом только в узловых точках. Рассмотрим в качестве примера расчет с помощью МКЭ осевого растяжения ступенчатого стержня /Каплун/. Ступенчатый стержень жестко заделан с левого края и имеет сечения А1 и А2, нагружен с правого торца растягивающим усилием Р. Требуется определить перемещение сечений 1,2,3 (рис. 15).
Рис. 15 Ступенчатый стержень Разобьем стержень на два элемента (I, II) так чтобы граница между элементами проходила в месте изменения перпендикулярного к длине сечения стержня. Введем на границах элементов узлы 1,2,3 в которых будем искать перемещения u. В результате такого упрощения мы будем решать задачу растяжения двух стержневых элементов каждый из которых имеет длину L, площадь (А) приложенное к узлам усилие (Р1и Р2) и смещения (u1,u2) которые появляются от действия этого усилия рис. 16.
Рис 16 – Элемент стержня. Для любого из этих P1 = P2 = где Е модуль упругости или модуль юнга. Для элемента систему узловых усилий можно записать следующим образом:
Рассмотрим (1) более подробно в нем Вертимся к ступенчатому стержню очевидно, что поскольку стержень состоит из нескольких элементов, то для решения задачи необходимо объединить соотношения для элементов 1 и 2. Тогда можно записать
Где в векторе усилий У нас осталось неиспользованное ограничение по перемещению (u1=0). Его можно использовать для упрощения решения системы. Если заменить в матрице жесткости первую строку и первый столбец на нули а элемент матрицы стоящий на главной диагонали заменить на единицу. Тогда уравнение примет вид:
решением этого уравнения являются следующие значения перемещений. u1=0, u2=
Пространственное положение каждого из элементов системы описывается с помощью числа степеней свободы В приведенном примере одного растяжения стержня решение системы уравнений (1) может быть получено просто в явном виде. В случае моделирования поведения более сложных тел приходится, задаваясь значениями перемещений искать решение системы (2) так чтобы выполнялось условие минимизации. В ходе такого решения значениями перемещений приходиться задаваться неоднократно, поэтому МКЭ носит название вариационного метода. Как правило, для расчетов соотношения между перемещением и усилием Такая форма записи используется при описании последовательно протекающих в теле процессов. Условие минимизации энергии можно получить, если в условии (1) перенести вектор сил в правую часть и устремить разность к нулю:
Рассматриваемый нами пример позволяет определить напряжено-деформированое состояние тела на основании варьирования перемещений. В действительности термин МКЭ определяет более широкий набор математических способов расчета. Среди которых в зависимости от вариационного перемещения можно выделить следующие: В перемещениях (минимум потенциальной энергии Лагранжа) – варьируются В напряжениях (минимум дополнительной работы Кастильо) – варьируются напряжения. Смешанные (принцип Райснера) – варьируются перемещения и напряжения. Гибридные (принцип Ху-Вашицу) – варьируются перемещения, напряжения и деформации. Наиболее часто используется принцип Лагранжа. В зависимости от области науки, в которой используются МКЭ функций смысл векторов, Таблица 1 – физический смысл векторов u и F
Лекция 8 Общая схема алгоритма расчета с помощью МКЭ. I. Создание ГМ и ее дискретизация. 1. Создание геометрической модели. 2. Задание типа КЭ. 3. Создание сетки КЭ. II. Задание граничных условий. 1. Задание условий закрепления. 2. Задание условий симметрии. 3. Задание условий приложения нагрузок. 4. Задание контактных условий. Взаимодействие. III. Задание свойств материала. IV. Выбор параметров расчета. 1. Задание типа расчета. 2. Задание условий расчета. 3. Задание условий остановки расчета. V. Осуществление расчета (автоматически). VI. Анализ полученных результатов. 1. Выявление ошибок расчета. 2. Принятие решения о повторном расчете.
Создание геометрической модели. Для решения любой задачи ОМД на компьютере необходимо, прежде всего, создать геометрическую модель, описывающую пространственными характеристиками моделируемого объекта. Геометрическая модель может быть построена как собственными средствами программы инженерных расчетов (CAE-системы) так и в другой программе специализирующиеся на создании геометрических моделей, (в роли таких программ выступают CAD-системы) как правило, CAD системы имеют больше возможностей для геометрического моделирования. Для переноса геометрической модели из CAD системы в CAE систему используются специальные форматы (STL, AGES, и др). Построенная геометрическая модель, как правило, является непрерывной и определяется либо с помощью сплошного объекта либо с помощью поверхностей. Такая модель для использования в расчетах должна быть дескретизирована. Процесс дискретизации исходно непрерывной модели может быть сведен к двум этапам: На первом этапе осуществляется выбор КЭ с помощью которых будет описываться геометрическая модель. На втором – объединение КЭ в сетку или ассомблирование с математической точки зрения процесс ассамблирования заключается в объединении матриц жесткости отдельных КЭ в глобальную матрицу жесткости всего тела. Для осуществления ассамблирования используются нумерации узлов внутри каждого КЭ и глобальная нумерация узлов. При этом между глобальной и локальной нумерацией узлов существует однозначное соответствие. Можно ли осуществлять сразу построение дискретной модели? Можно, но этот процесс применяется редко из-за его сложности.
Атрибуты КЭ Как отмечалось ранее основой для решения задач с помощью МКЭ является замена сплошного тела математической моделью, которая состоит из непересекающихся более простых КЭ. Каждый КЭ описывается с помощью значений сплошной функции в узлах КЭ (степеней свободы). Поведение математической модели в целом зависит от поведения отдельных КЭ и их объединения в дискретную модель (ассамблирования) /Лекции МКЭ/. Рассмотрим свойства (атрибуты) КЭ. В зависимости от размерности исследуемой задачи и принимаемых допущений КЭ можно разделить /Лекции МКЭ, Рычнов.186,Каплун/ Одномерные элементы – имеют форму линии, используются для описания поведения таких конструктивных элементов как стержни, балки и т.д. В задачах ОМД практически не используются, рис 1а. · Двумерные элементы – как правило, имеют трех угольную или четырех угольную форму. Используются для описания плоских тел, у которых одно измерение значительно меньше двух других. · Применяются для описания деформируемых тел ЛШ или для описания задач, которые можно упростить до уровня расчета в плоскости осесимметричные и с постоянным в плане сечением задачи, рис 1б. · Трехмерные элементы – имеют форму тетраэдров и гексаэдров. Используются для описания объекта тел, для описания большинства задач ОМД, рис 1в
Рис. 17 – типы КЭ в зависимости от размерности: а – одномерные; б – двумерные; в – трехмерные.
Показанные на рис. 17 элементы имеют прямолинейные ребра и называются линейной функцией, поэтому не всегда достаточно точно описывают особенности поведения исследуемой функции рис. 18.На рис 2 показана функция перемещений КЭ при заполнении радиусного участка гравюры штампа. Плоское ребро “мешает” точно описать геометрию штампа. Поэтому для описания апроксемирующей функции элемента (функции формы) используют полиномы более высоких степеней второй или третьей.
Рис. 18 – Аппроксимация гравюры штампа: а –линейными КЭ; б – квадратичными КЭ. Таким образом, в зависимости от используемой функции формы КЭ делятся на: · Линейные – описываются …… 1 степени ребро образовано двумя узлами рис.а. · Квадратичные – 2 степени – тремя узлами рис 3б. · Кубические – 3 степени – четырьмя узлами рис 3в.
Рис. 19 – Типы конечных элементов в зависимости от используемой функции формы: а – линейные; б – квадратичные; в – кубические.
По расположению узловых точек элемента бывают обычные и вырожденные элементы. Вырожденные элементы это элементы которые в следствии непрерывной дискретизации приняли форму у которой часть узлов совпала. Возникают такие элементы в следствии разбиения сплошных геометрических участков или в местах перехода от более крупной сетки к более мелкой. Могут служить источниками неоднозначности и ошибок расчетов. Каждый КЭ обладает конечном количеством степеней свободы, которые определяют состояние элемента или физическое поле колода описывает данный элемент. За счет общих степеней свободы в узлах соседних элементов осуществляется ассамблирование КЭ в дискретную модель. В зависимости от того, какие степени свободы используются для задания значений исследуемой функции различают Лагранжевы и Эрмитова элементы. В Лагранжевых элементах в качестве степеней свободы выступают значения функции перемещения в узлах. В Эрмитовых – производные этой функции по пространственным координатам. Каждый элемент обладает также свойством материала. При описании свойств материала используются различные модели рассмотренные ранее. В зависимости от вида приложения и решаемых в нем задач могут использоваться различные типы КЭ. В ряде случаев КЭ могут содержать свойства нескольких более простых КЭ. Такие элементы называют макроэлементами, они позволяют описывать поведение текстурированных и композиционных материалов.
Построение сетки КЭ (ассамблирование). Важным этапом моделирования с помощью МКЭ является дискретизация или построение сетки конечных элементов КЭ. Обычно в современных программных продуктах реализуется несколько вариантов построения сетки КЭ (в дальнейшем просто сетки). Поскольку увеличение возможностей создания сетки дает инженеру, использующему программу более гибкий инструмент для решения более широкого класса задач. Явное и неявное моделирование. Практически все программные продукты в настоящий момент имеют автоматический генератор сетки, который может создавать сетку либо по количеству КЭ, либо по заданной пользователем величине ребра КЭ. При этом сетка может быть как упорядоченной (когда КЭ обладают определенной формой и размерами в близи друг друга) или произвольной, свободной (при этом размеры соседних КЭ могут значительно отличаться друг от друга). Очевидна взаимосвязь между количеством КЭ в сетке и их размерами: количество КЭ в модели определяет их размеры и наоборот размер КЭ определяет их количество в сетке. Очевидно, также и то, что чем больше число КЭ в сетке, тем дольше ЭВМ будет осуществлять вычисления. При этом с ростом числа КЭ будет расти и погрешность вычисления связанная с погрешностью округления результатов расчета на ЭВМ. С другой стороны грубое описание исходной геометрической модели крупной сеткой тоже создает значительные ошибки. Следовательно, ошибка вычисления всегда будет присутствовать независимо от размера КЭ.
Рис. 20 – Иллюстрация к погрешности вычисления с помощью МКЭ: Δ – ошибка; T – время расчета; h – размер ребра КЭ применяемого для расчета. С другой стороны грубая сетка дает заниженный на 20-40% результат рассчитанных напряжений, что необходимо учитывать. /Статья с сайта Ansys/ Обычно при моделировании с помощью МКЭ поступают в соответствии с методом последовательного приближения: сначала осуществляют расчет на более грубой сетке, т.е. сетке с малым количеством КЭ, затем, получив предварительные расчеты, увеличивают количество конечных элементов и рассчитывают задачу снова, полученные данные анализируют, если разница, полученная в результате двух последних расчетов отличается менее чем на инженерную погрешность (5%) то для анализа результатов моделирования используют вариант с последней рассчитываемой сеткой. Согласно рекомендациям /Каплун/ при выборе КЭ для сетки необходимо учитывать то что: · линейные элементы требуют более частой сетки, чем квадратичные (с одним промежуточным узлом) или кубические (с двумя промежуточными узлами); · упорядоченная сетка является более предпочтительной, чем произвольная; · прямоугольная сетка с 4 узлами более предпочтительна, чем сетка с треугольными элементами; · сетка прямоугольных элементов с промежуточными узлами имеет туже точность, что и сетка прямоугольных элементов с 4 узлами; · прямоугольная сетка с 8 узлами является более предпочтительной, чем сетка треугольных элементов с промежуточными узлами, несмотря на большой размер прямоугольных элементов; аппроксимация смещений кубическим полиномом не требует более мелкой сетки. Поскольку точность расчета напрямую зависит от того, какие размеры имеет КЭ то необходимо придерживаться следующих рекомендаций: В тех местах, где ожидаются большие величины напряжений деформаций необходимо, чтобы сетка была более плотной, обычно такие места на заготовке соответствуют концентраторам напряжений на инструменте. С другой стороны в местах, где не ожидается интенсивное течение металла и больших давлений сетка может иметь большие размеры КЭ. В соответствие с требованиями /Deform/ при построении сетки для корректного описания геометрической модели размеры КЭ сетки должны быть минимум в три раза меньше чем наименьший концентратор напряжений на данном участке. Данное требование создает необходимость строить сетки с большим количеством КЭ при наличии небольших концентраторов напряжений, что значительно усложняет моделирование процессов листовой штамповки, где для дискретизации при объемном решении задачи по толщине заготовки необходимо строить более трех элементов при значительной поверхности заготовки. При моделировании задач с объемным напряженным состоянием, например пробивки (вырубки), или чеканки количество КЭ в сетки можно уменьшить введением локального сгущения сетки. При этом сгущение сетки должно быть осуществлено таким образом, чтобы размеры соседних конечных элементов не превышали друг друга более чем в два раза /Каплун/. На точность расчета влияет также форма КЭ так по /Каплун/ нежелательно использовать в сетке конечные элементы, имеющие один из размеров значительно больше и меньше других размеров. Добб из Рычкова. Лекция 9 Граничные условия.
Граничные условия, используемые в математике можно разделить на два типа: искусственные и естественные. Естественные граничные условия накладываются на искомую функцию, в то время как существенные (искусственные) на ее производные. Естественные граничные условия появляются при работе с исходной математической моделью и существенные ставятся независимо от нее. С точки зрения МКЭ существенные граничные условия – это граничные условия, влияющие непосредственно на степени свободы модели. Естественные граничные условия влияют на степени свободы через глобальный вектор усилий. Существенные граничные условия накладываются на вектор степеней свободы, и поэтому, как правило, наиболее искусственным ограничением является ограничение по перемещению, которое может быть наложено в одном, двух или трех направлениях на узлы сетки. В теории упругости осевые ограничения называются также кинематическими. Примером в ОМД может быть ограничение течения металла через стену штампа создаваемое автоматически программой расчета или заделка или шарнир в прелагаемых расчетах. Естественные граничные условия накладываются на вектор усилий. К этим условиям относят различные внешние силовые воздействия, действующие на точки или поверхности тела. Обычно такие граничные условия называют силовыми граничными условиями. Примером в ОМД могут быть силовые условия деформирования металла. На практике приходится сталкиваться еще и со смешанными граничными условиями. В этом случае в данной точке поверхности тела задаются усилия и перемещения. Наиболее распространенный пример таких граничных условий это задание плоскостей геометрической симметрии при решении задач деформирования осесимметричных тел. При решении геометрии симметричных задач смешанные граничные условия заключаются в равенстве нулю нормальных перемещений и равенству нулю касательных сил. На практике задание любых граничных условий являются важным элементом моделирования. Задание граничных условий должно отвечать следующим требованиям. 1. Граничные условия не должны быть абсурдны по своей сути – например при изучении процесса прикладывать усилие и фиксировать перемещение в одном и том же направлении не имеет смысла, нет смысла также фиксировать все перемещения в узлах дискретной модели. (рис ХХ). 2. Соответствие действия граничных условий на реальном теле тому, как действуют граничные условия на модели – должно быть однозначное соответствие между усилиями и возможностями по перемещению модели и моделируемого объекта.
Рис. ХХ – Приложение граничных условий при осадке. Следует заметить то, что граничные условия прикладываются к узлам дискретной модели и наибольшее число граничных условий которое можно применить к каждому узлу это либо 3 силы, либо 3 перемещения. Число граничных условий должно быть обоснованно и минимально необходимо /Каплун/. Задание ограничений в современных программах очень упрощенно, например, для задания плоскостей симметрии при осадке достаточно указать поверхность симметрии на теле модели, а система сама распознает и накладывает ограничения на те узлы, которые принадлежат к этой плоскости. В случае использования программы граничные условия могут быть приложены к узлу, линии, поверхности или объему, но следует помнить, что с линии, поверхности и объема граничные условия будут перераспределенными на узлы.
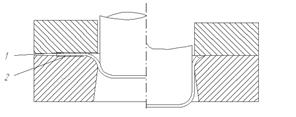
Решение контактных задач. Особенностью задач ОМД являются наличие больших контактных поверхностей. Следует заметить, что контактные задачи являются достаточно сложными задачами. Общая последовательность решения таких задач сводится к дополнительному заданию условий действующих нам контактных поверхностях. Очевидно что для задания этих условий необходимо как то определить саму контактную пару. Отличительной особенностью задач ОМД является то что в ходе технологии процесса контактная поверхность м/у инструментом и заготовкой претерпивает значительные изменения. Например в процессе принудительной вытяжки. Заготовка и матрица касаются по зоне 1, контакта м/у пуансоном и заготовкой нет, затем в зоне 2, происходит касание пуансона и заготовки при этом боковой поверхности матрицы и пуансона штампа нет. На следующем этапе возникает контакт в зоне 3 и 4 м/у матрицей и заготовкой. На следующем этапе контакт в зоне 1 исчезает.
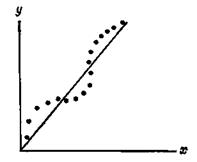
Рис. ХХ – Развитее зоны контакта на различных этапах вытяжки. Из приведенного примера понятно, что предугадать развитие зоны контакта достаточно сложно, поэтому средства позволяющие рассчитывать контактные задачи должны обеспечить решение в условиях этой неопределенности. Лекция 10 Обработка результатов эксперимента. Регрессионный и корреляционный анализ. МНК. При поиске функциональной связи между исследуемыми параметрами появляется необходимость ввести некоторую гипотезу о характере функциональной зависимости между параметрами, т.е. аппроксимировать ее некоторым относительно простым математическим выражением, например линейной квадратичной и экспоненциальной зависимостями. Для поиска таких функциональных математических зависимостей между двумя или более переменными по накопленным экспериментальным данным используются методы регрессионного и корреляционного анализа. Регрессионный анализ дает возможность построить исходя из имеющихся совокупности экспериментальных данных, уравнение, вид которого задает аналитик, а корреляционный анализ позволяет судить о том, насколько хорошо экспериментальные точки согласуется с выбранным уравнением (“ложатся” на соответствующую кривую). Первым шагом при выводе уравнения, аппроксимирующего (описывающего) требуемую зависимость, является сбор данных, отражающих соответствующие значения рассматриваемых переменных. Следующим шагом будет нанесение этих точек (x1;y1), (х2;у2),, (xN;yN) на график в прямоугольной системе координат. В результате мы получим так называемую диаграмму разброса, из которой часто удается визуально найти вид плавной кривой, аппроксимирующей функциональную зависимость и обнаружить “промахи”. Задача нахождения для аппроксимирующих кривых таких уравнений, которые наилучшим образом отображают данную совокупность экспериментальных точек, называется задачей подгонки кривых по точкам. Прежде всего, аналитик должен выбрать вид кривой, для которой он будет искать аппроксимирующее уравнение. Эта кривая должна “наилучшим” образом описывать экспериментальную зависимость. Наиболее распространенный метод, по которому можно определить параметры уравнения аппроксимации – метод наименьших квадратов (МНК). Данный метод формализует процедуру подбора аппроксимирующей кривой на глаз, когда мы, стремимся свести к минимуму отклонения экспериментальных точек от подбираемой кривой. Поясним это примером. На рис.2, где через (х1,y1), (х2,у2), … (хn,уn) обозначены координаты экспериментальных точек, для любого заданного х, будет иметь место разница между у1 и соответствующим значением, получающимся по теоретической кривой. Обозначим эту разницу символом D1, и будем называть ее отклонением. Это отклонение может быть положительным, отрицательным или нулевым. Соответственно для каждой из экспериментальных точек можно вычислить значения отклонений D2,..., DN. Тогда мерой качества приближения кривой к экспериментальным данным можно считать сумму абсолютных отклонений, т. е. |D1| + |D2|+ …+|Dn|.
Рис.2 – Пояснения к методу наименьших квадратов. Поскольку отклонения могут быть положительными или отрицательными, с математической точки зрения проще возвести их значения в квадрат и в дальнейшем иметь дело с квадратичными отклонениями. Их сумма даст такую же хорошую меру качества приближения. Будем поэтому считать, что из всех возможных аппроксимирующих кривых кривой наилучшего приближения для данной совокупности экспериментальных точек будет та, для которой сумма D12+D22+…+DN2 минимальна. Так определяется критерий наилучшего приближения по методу наименьших квадратов. Математический метод, обеспечивающий такую подгонку выбранной кривой, при которой экспериментальные точки ложатся на нее наилучшим образом называется регрессионным анализом. Общий вид кривой наилучшего приближения аналитик выбирает по результатам изучения диаграммы разброса. Здесь свобода выбора полностью принадлежит исследователю (в работе будут рассмотрены линейная, квадратичная и экспоненциальная зависимости). Используемый математический аппарат должен обеспечивать наилучшее приближение кривой к экспериментальным данным. При этом не важно насколько правильно аналитически выбран вид кривой. Под приближением кривой к экспериментальным данным мы понимаем только процесс вычисления значений констант или параметров, таким образом, чтобы сумма квадратичных отклонений была минимальной. Наилучшее приближение регрессионной кривой к экспериментальным данным вовсе не означает, что реально существующая физическая зависимость наилучшим образом описывается аппроксимирующим уравнением, соответствующим именно этой прямой. Математические операции лишь приводят к значениям параметров, обеспечивающим наилучшее приближение к уравнению выбранного вида. Наглядный этому пример дает рис.3.
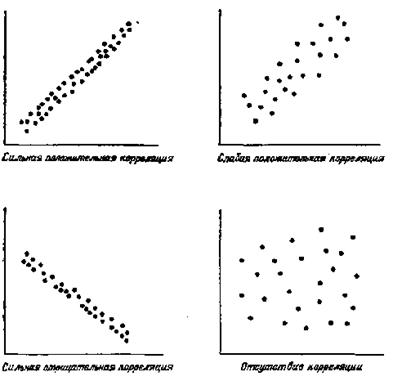
Рис.3 – Иллюстрация к корреляционному анализу. Для оценки того, насколько хорошо регрессионная прямая (уравнение прямой) в действительности согласуется с экспериментальными данными, вводится понятие корреляции. Это понятие дает возможность судить о том, насколько тесно ложатся экспериментальные точки на аппроксимирующую кривую. Если регрессия определяет предполагаемое соотношение между переменными, то корреляция показывает, насколько хорошо это соотношение отражает действительность. Сильная корреляция между переменными означает, что их изменения взаимосвязаны (рис.4), однако необходимо иметь в виду, что это еще не доказывает наличия причинно-следственной связи между переменными. Корреляция говорит лишь о том, насколько тесно экспериментальные точки ложатся на аппроксимирующую кривую. Но она не может сказать, справедливо ли основное допущение о наличии причинно-следственной связи. Корреляционный анализ показывает лишь степень соответствия данных принятой гипотезе. Для оценки значимости корреляции вводят коэффициент корреляции. На рис.4 приведены примеры для анализа коэффициента корреляции. Коэффициент корреляции лежит в пределах от -1 до +1. Коэффициент -1 соответствует максимальной отрицательной корреляции, когда у уменьшается с увеличением х, а все экспериментальные точки лежат точно на кривой. Коэффициент 0 соответствует полному отсутствию корреляции когда зависимости между величинами х и у нет, а коэффициент +1 — максимальной положительной корреляции. Чем ближе значение R к единице (неважно, с каким знаком), тем с большей уверенностью можно утверждать, что между интересующими нас переменными существует связь, т. е. что значение какой-то одной из этих переменных существенным образом зависит от того, какое значение принимает другая переменная. На практике не приходится надеяться на то, что получится единица, или ноль. Поэтому для того чтобы определить значимость коэффициента корреляции, необходимо знать его критическое значение. Процедура сопоставления вычисленной характеристики с табличным критическим значением называется проверкой гипотезы.
Рис.4 – Виды экспериментальных графиков при различных значениях коэффициента корреляции. Лекция 11 Планирование эксперимента. Введение Первая работа в области ПЭ была опубликована в 1951 г. Боксом и Уилсоном в Англии. Их идея проста: экспериментатор ставит последовательно небольшие серии опытов, в каждой из которых одновременно варьируются по определенным правилам все факторы. Серии организуются таким образом, что после математической обработки предыдущей, можно было выбрать условия проведения, т.е. спланировать следующую серию. Так, последовательно, шаг за шагом, достигается область оптимума.
|

 а)
а) 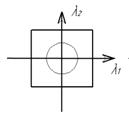 б)
б) 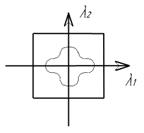 в)
в)
 Тензор
Тензор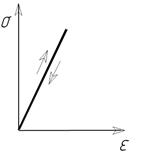 а)
а) 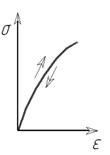 б)
б)  в)
в)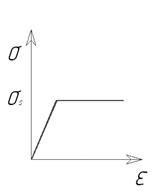 а)
а) 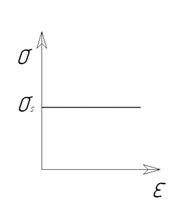 б)
б)  в)
в)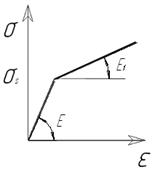
 б)
б)
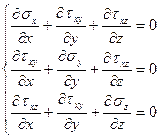
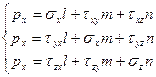

 элементов согласно теории сопротивления материалов можно записать значения усилия действующего в узлах.
элементов согласно теории сопротивления материалов можно записать значения усилия действующего в узлах.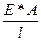 (u1 – u2);
(u1 – u2);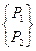 =
= 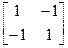
 или
или 
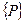 =
= 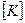
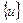 (1)
(1)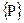 называется матричным вектором усилий,
называется матричным вектором усилий, 
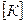 – матрицей жесткости.
– матрицей жесткости.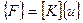 или
или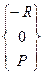 =
= 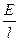
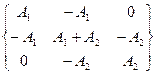

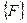 уже учтено, то что R является реакцией опоры приложенной в узле 1, а Р является растягивающим усилием приложенным в узле 3, а узел 2
уже учтено, то что R является реакцией опоры приложенной в узле 1, а Р является растягивающим усилием приложенным в узле 3, а узел 2 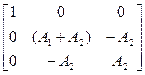
 ; u3=
; u3= 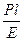
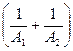
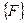 на вектор степеней свободы
на вектор степеней свободы  записываются в виде (1). Но при необходимости вектор усилий
записываются в виде (1). Но при необходимости вектор усилий 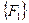 и вектор механических сил
и вектор механических сил  тогда (1) можно переписать в виде
тогда (1) можно переписать в виде 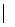 K
K 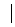 EИ
EИ 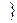 =
= 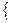 FТ
FТ  И
И 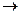 0 (2)
0 (2)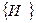 и
и 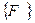 может измениться см. табл. 1.
может измениться см. табл. 1. а)
а) 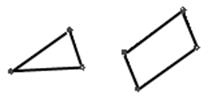 б)
б) 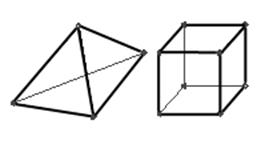 в)
в)
 а)
а)  б)
б)  в)
в)