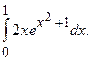Задача №1
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ МНОГОЧЛЕНА НЬЮТОНА
Задание. Дана таблица значений функции  . Построить для этой функции интерполяционный многочлен Ньютона и с его помощью найти приближенное значение функции для заданного аргумента
. Построить для этой функции интерполяционный многочлен Ньютона и с его помощью найти приближенное значение функции для заданного аргумента  .
.
| №1.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 0.740
| 0.532
| 0.801
| 1.13
| 0.749
|
|
| №2.
| X
| 2.5
| 3.0
| 3.5
| 4.0
| 4.5
| 
|
| Y
| 0.912
| 0.755
| 0.96
| 0.524
| 0.574
|
|
| №3.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
| 0.741
| 0.848
| 0.809
| 0.854
| 0.801
|
|
| №4.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 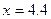
|
| Y
| 0.567
| 0.759
| 0.991
| 1.57
| 0.532
|
|
| №5.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 1.59
| 0.935
| 0.596
| 1.78
| 0.682
|
|
| №6.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
| 0.707
| 0.790
| 1.11
| 0.674
| 0.948
|
|
| №7.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 0.751
| 0.964
| 0.927
| 0.780
| 0.585
|
|
| №8.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 0.622
| 0.720
| 1.05
| 0.831
| 1.69
|
|
| №9.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 0.814
| 0.749
| 0.789
| 0.979
| 0.682
|
|
| №10.
| X
| 1.0
| 1.5
| 2.0
| 2.5
| 3.0
| 
|
| Y
| 0.865
| 1.83
| 0.521
| 0.889
| 0.800
|
|
| №11.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 0.664
| 1.30
| 0.880
| 0.764
| 0.981
|
|
| №12.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 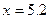
|
| Y
| 0.710
| 0.991
| 0.501
| 0.892
| 0.735
|
|
| №13.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| 0.964
| 0.714
| 0.644
| 0.674
| 1.04
|
|
| №14.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
| 0.892
| 0.760
| 1.26
| 0.585
| 1.74
|
|
| №15.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
| 0.778
| 1.17
| 0.933
| 0.772
| 0.836
|
|
| №16.
| X
| 4.5
| 5.0
| 5.5
| 6.0
| 6.5
| 
|
| Y
| 1.01
| 0.726
| 0.798
| 0.569
| 0.842
|
|
| №17.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
| 0.770
| 0.825
| 1.35
| 0.775
| 1.79
|
|
| №18.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
| 0.671
| 0.969
| 0.667
| 0.589
| 0.922
|
|
| №19.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
| 0.594
| 0.601
| 0.840
| 0.517
| 1.94
|
|
| №20.
| X
| 3.0
| 3.5
| 4.0
| 4.5
| 5.0
| 
|
| Y
| 1.19
| 0.671
| 0.542
| 0.750
| 0.775
|
|
Задача №2
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Задание. Дана таблица значений функции  . Используя метод наименьших квадратов, подобрать для заданных значений
. Используя метод наименьших квадратов, подобрать для заданных значений  и
и 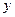
1) линейную функцию  ;
;
2) квадратичную функцию  .
.
Построить графики этих функций.
| №1.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| -1
|
|
|
|
|
|
| №2.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 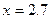
|
| Y
|
|
| -1
|
|
|
|
| №3.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
|
|
|
| -1
| -4
|
|
| №4.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
|
|
|
|
| -1
|
|
| №5.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
|
|
| -2
|
|
|
|
| №6.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
|
|
|
| -1
|
|
|
| №7.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
|
|
|
|
| -2
|
|
| №8.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
|
| -2
|
|
|
|
|
| №9.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
|
|
|
|
| -1
|
|
| №10.
| X
| 1.0
| 1.5
| 2.0
| 2.5
| 3.0
| 
|
| Y
|
|
| -1
|
|
|
|
| №11.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
|
|
| -2
|
|
|
|
| №12.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 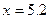
| |
| Y
|
|
|
|
| -1
|
| |
| №13.
| X
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
| 
|
| Y
| -2
|
|
|
|
|
|
| №14.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
|
|
|
| -1
| -2
|
|
| №15.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
|
|
|
|
| -1
|
|
| №16.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
| -1
|
|
|
|
|
|
| №17.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 
|
| Y
|
| -1
|
|
|
|
|
| №18.
| X
| 4.0
| 4.5
| 5.0
| 5.5
| 6.0
| 
|
| Y
| -2
|
|
|
|
|
|
| №19.
| X
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 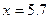
|
| Y
|
|
|
|
| -1
|
|
| №20.
| X
| 3.0
| 3.5
| 4.0
| 4.5
| 5.0
| 
|
| Y
|
| -2
|
|
|
|
|
Задача №3
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Задание. Получить приближенное решение системы методом простой итерации с точностью 0.01.
№1.  №2.
№2. 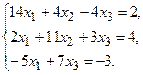
№3.  №4.
№4. 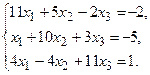
№5. 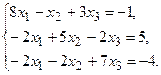 №6.
№6. 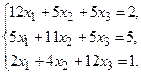
№7.  №8.
№8. 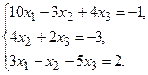
№9. 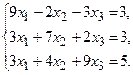 №10.
№10. 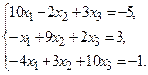
№11.  №12.
№12. 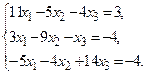
№13.  №14.
№14. 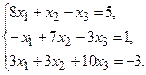
№15.  №16.
№16. 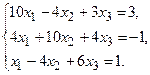
№17. 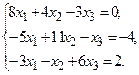 №18.
№18. 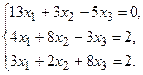
№19. 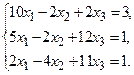 №20.
№20. 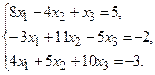
Задача №4
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Задание. Отделить корни и найти приближенное решение заданного уравнения с точностью 0.01 методом Ньютона (вариант 1-10) и методом итераций (вариант 11-20).
№1.  №2.
№2. 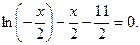
№3. 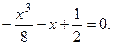 №4.
№4. 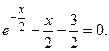
№5. 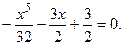 №6.
№6. 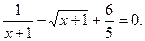
№7.  №8.
№8. 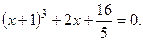
№9.  №10.
№10. 
№11.  №12.
№12. 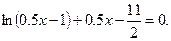
№13.  №14.
№14. 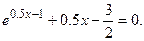
№15. 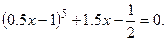 №16.
№16. 
№17. 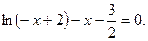 №18.
№18. 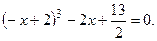
№19.  №20.
№20. 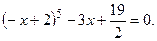
Задача №5
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Задание. 1) Вычислить интеграл по формуле трапеций с тремя десятичными знаками после запятой.
2)Вычислить интеграл по формуле Симпсона при  . оценить погрешность результата, составив таблицу конечных разностей.
. оценить погрешность результата, составив таблицу конечных разностей.
№1.  №2.
№2. 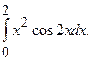
№3.  №4.
№4. 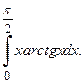
№5.  №6.
№6. 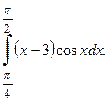
№7.  №8.
№8. 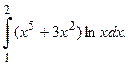
№9.  №10.
№10. 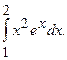
№11.  №12.
№12. 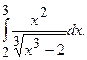
№13.  №14.
№14. 
№15.  . №16.
. №16. 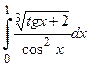 .
.
№17. 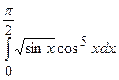 №18.
№18. 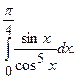
№19.  №20.
№20. 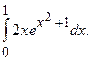
Задача №6
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

 . Построить для этой функции интерполяционный многочлен Ньютона и с его помощью найти приближенное значение функции для заданного аргумента
. Построить для этой функции интерполяционный многочлен Ньютона и с его помощью найти приближенное значение функции для заданного аргумента  .
.


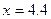






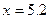








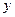
 ;
; .
.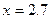


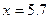
 №2.
№2. 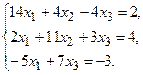
 №4.
№4. 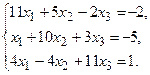
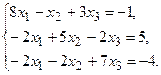 №6.
№6. 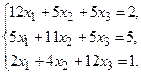
 №8.
№8. 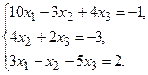
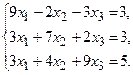 №10.
№10. 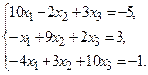
 №12.
№12. 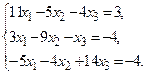
 №14.
№14. 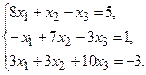
 №16.
№16. 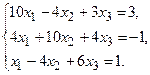
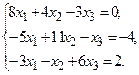 №18.
№18. 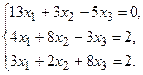
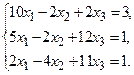 №20.
№20. 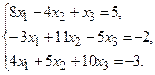
 №2.
№2. 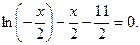
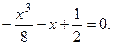 №4.
№4. 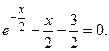
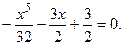 №6.
№6. 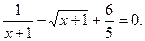
 №8.
№8. 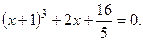
 №10.
№10. 
 №12.
№12. 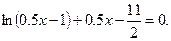
 №14.
№14. 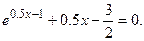
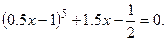 №16.
№16. 
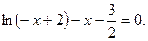 №18.
№18. 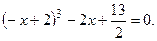
 №20.
№20. 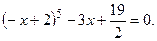
 . оценить погрешность результата, составив таблицу конечных разностей.
. оценить погрешность результата, составив таблицу конечных разностей. №2.
№2. 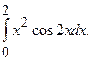
 №4.
№4. 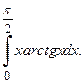
 №6.
№6. 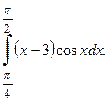
 №8.
№8. 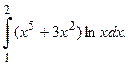
 №10.
№10. 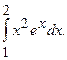
 №12.
№12. 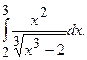
 №14.
№14. 
 . №16.
. №16. 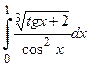 .
.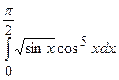 №18.
№18. 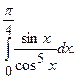
 №20.
№20.