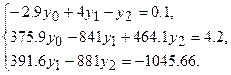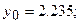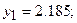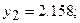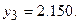= 0,
= 0,
где  - непрерывная функция переменной
- непрерывная функция переменной  . Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займемся их приближенным вычислением с заданной точностью.
. Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займемся их приближенным вычислением с заданной точностью.
Основные этапы решения. Решение задачи отыскания корней осуществляется в два этапа. Первый этап называется этапом отделения (локализации) корней, второй – этап итерационного уточнения корней.
Известно, что если функция  непрерывна и принимает на концах отрезка
непрерывна и принимает на концах отрезка  значения разных знаков, т.е.
значения разных знаков, т.е.  , то внутри этого промежутка имеется хотя бы один корень уравнения.
, то внутри этого промежутка имеется хотя бы один корень уравнения.
Геометрически это означает, что график непрерывной функции, расположенной по разные стороны оси  , пересекает эту ось, по меньшей мере в одной точке.
, пересекает эту ось, по меньшей мере в одной точке.
Отрезок  , содержащий только один корень уравнения
, содержащий только один корень уравнения  , называется отрезком локализации корня. Цель этапа локализации считается достигнутой, если для каждых подлежащих определению корней удалось указать отрезок локализации.
, называется отрезком локализации корня. Цель этапа локализации считается достигнутой, если для каждых подлежащих определению корней удалось указать отрезок локализации.
К сожалению, создать универсальный метод локализации не представляется возможным. В простых ситуациях хороший результат может давать графический метод. Часто применяется построение таблиц значений функции вида 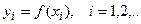 и, при этом о наличии корня на отрезке
и, при этом о наличии корня на отрезке  , судят по перемене знака функции на концах отрезка.
, судят по перемене знака функции на концах отрезка.
Пример 1. Локализуем корни уравнения
 .
.
Для этого преобразуем уравнение к виду  и построим графики функций
и построим графики функций  и
и  .
.
Абсциссы точек пересечения этих графиков являются корнями данного уравнения.
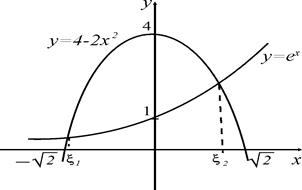
Рис. 1
Из рис.1 видно, что уравнение имеет два корня, расположенные на отрезках  и
и  .
.
Пример 2. Локализуем корни уравнения
 .
.
Для этого составим таблицу значений функции 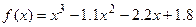 на отрезке
на отрезке  с шагом
с шагом
| x
| -2
| -1.6
| -1.2
| -0.8
| -0.4
|
| y
| -6.2
| -1.592
| 1.128
| 2.344
| 2.44
|
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
|
| 1.8
| 0.808
| -0.152
| -0.696
| 
|
|
Из таблицы видно, что функция  меняет знак на концах отрезков
меняет знак на концах отрезков 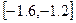 ,
,  ,
,  . Поэтому каждый из этих отрезков содержит хотя бы один корень. Поскольку
. Поэтому каждый из этих отрезков содержит хотя бы один корень. Поскольку  – многочлен третьей степени, то он не может иметь больше трех корней. Поэтому задача локализации корней решена.
– многочлен третьей степени, то он не может иметь больше трех корней. Поэтому задача локализации корней решена.
После локализации корней производится итерационное уточнение каждого корня одним из существующих методов. Мы рассмотрим метод касательных и метод итераций.
1) Метод касательных. Если известно хорошее начальное приближение решения уравнения  , то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности
, то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности  .
.
Достаточные условия сходимости этого метода содержатся в следующей теореме.
Теорема. Пусть функция  определена и дважды дифференцируема на отрезке
определена и дважды дифференцируема на отрезке  , причем
, причем  , а производные
, а производные  сохраняют знак на отрезке
сохраняют знак на отрезке  . Тогда, исходя из начального приближения
. Тогда, исходя из начального приближения 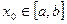 , удовлет-воряющего неравенству
, удовлет-воряющего неравенству  , можно построить последовательность
, можно построить последовательность  сходящуюся к единственному на
сходящуюся к единственному на  решению
решению  уравнения
уравнения  .
.
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой  касательной, проведенной в некоторой точке кривой (рис. 2).
касательной, проведенной в некоторой точке кривой (рис. 2).
Выберем, например,  , для которого
, для которого  . Проведем касательную к кривой
. Проведем касательную к кривой  в точке
в точке 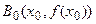 . В качестве первого приближения
. В качестве первого приближения  корня
корня  возьмем абсциссу точки пересечения этой касательной с осью
возьмем абсциссу точки пересечения этой касательной с осью  . Через точку
. Через точку  снова проведем касательную, абсцисса точки пересечения которой даст второе приближение
снова проведем касательную, абсцисса точки пересечения которой даст второе приближение  корня
корня  и т. д. (рис. 2).
и т. д. (рис. 2).
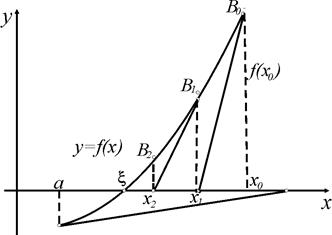
Рис. 2
Обозначим  .Найдем производную данной функции
.Найдем производную данной функции  .
.
Составим таблицу знаков функции:
Уравнение имеет действительный корень, лежащий в промежутке  . Уточним этот корень методом касательных. Так как
. Уточним этот корень методом касательных. Так как 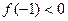 ,
, 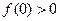 и
и  , то за начальное приближение принимаем
, то за начальное приближение принимаем  .
.
Для вычислений применяем формулу Ньютона
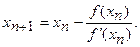
Для вычислений используем таблицу 3:
Таблица 3

| 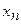
| 
| 
| 
|
|
| -1
-0.949
-0.9464
| -0.2
-0.0093
-0.0004
| 3.9
3.5814
3.5657
| -0.051
-0.0026
-0.00001
|
Ответ:  .
.
2) Метод итераций. Отделяем корни аналитически. Находим 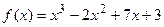 .
.
Составим таблицу знаков функции:
Уравнение имеет действительный корень, лежащий в промежутке  . Для уточнения его методом итераций приведем уравнение к виду
. Для уточнения его методом итераций приведем уравнение к виду  . При этом должно выполняться условие
. При этом должно выполняться условие  для
для  . Функцию
. Функцию  будем искать из соотношения
будем искать из соотношения  , считая, что
, считая, что  , где
, где  число
число  имеет тот же знак, что и
имеет тот же знак, что и  в промежутке
в промежутке  . Находим
. Находим 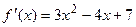 .
.
Так как  , то можно взять
, то можно взять 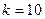 . Тогда
. Тогда
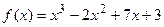
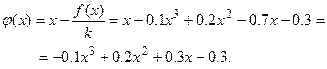
Пусть  , тогда
, тогда  . Вычисления располагаем в таблице 4.
. Вычисления располагаем в таблице 4.
Таблица 4

| 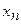
| 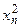
| 
| 
|
|
|
-0.3
-0.3693
-0.3785
-0.3795
0.3796
|
0.09
0.1364
0.1433
0.1440
|
-0.027
-0.0504
-0.0542
-0.0546
| -0.3
-0.3693
-0.3785
-0.3795
-0.3796
|
Ответ:  .
.
Задача №5
Задание. 1) Вычислить интеграл по формуле трапеций с тремя десятичными знаками.
2)Вычислить интеграл по формуле Симпсона при 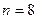 ; оценить погрешность результата, составив таблицу конечных разностей.
; оценить погрешность результата, составив таблицу конечных разностей.
1)  ; 2)
; 2)  .
.
Решение. Точное значение определенного интеграла вычисляется по формуле Ньютона-Лейбница через первообразную  :
:
 .
.
Если же первообразная неизвестна или функция задана таблицей или графиком, то применяются методы приближенного интегрирования. Формулы для приближенного интегрирования получаются при замене площади криволинейной трапеции на сумму площадей простых геометрических фигур, площадь которых легко вычисляется.
Разделим интервал  на
на  равных частей длиной
равных частей длиной  . При этом
. При этом  . Обозначим через
. Обозначим через  значение функции
значение функции  в точках
в точках  .
.
Метод трапеций. Если площадь каждой полоски, на которые разбита криволинейная трапеция точками  , считать приближенно равной площади соответствующей трапеции, то для вычисления интеграла получаем формулу трапеций (рис. 3)
, считать приближенно равной площади соответствующей трапеции, то для вычисления интеграла получаем формулу трапеций (рис. 3)
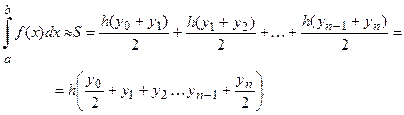
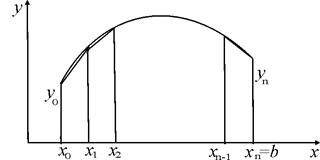
Рис. 3
Метод Симпсона. Метод Симпсона применим при разбиении интервала  на четное число частей
на четное число частей  . Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 4).
. Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 4).
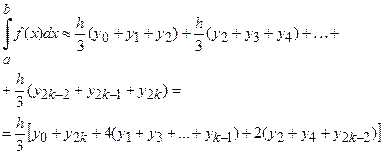
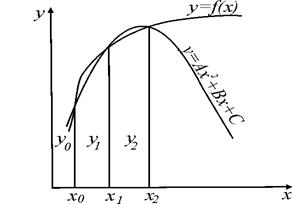
Рис. 4
1) Для достижения заданной степени точности необходимо определить значение  так, чтобы
так, чтобы
 (*)
(*)
Здесь  ;
;  ;
; 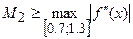 , где
, где  .
.
Находим  ,
,  ;
;
 .
.
Положим  , тогда неравенство (*) примет вид
, тогда неравенство (*) примет вид  , откуда
, откуда  , т.е.
, т.е.  ; возьмем
; возьмем  .
.
Вычисление интеграла проводим по формуле
 ,
,
где 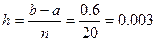 ;
;  ;
; 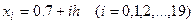 .
.
Все вычисления приведены в таблице 5:
Таблица 5

| 
| 
|
|
| 0.7
0.73
0.76
0.79
0.82
0.85
0.88
0.91
0.94
0.97
1.00
1.03
| 0.88386
0.85572
0.82898
0.80366
0.77973
0.75700
0.73546
0.71501
0.69551
0.67700
0.65937
0.64259
|
Продолжение табл. 5
|
| 1.06
1.09
1.12
1.15
1.18
1.21
1.24
1.27
1.30
| 0.62657
0.61140
0.59669
0.58272
0.56935
0.55658
0.54431
0.53253
0.52129
|
Таким образом,
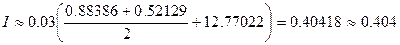 .
.
2) Согласно условию 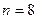 , поэтому
, поэтому  .
.
Расчетная формула имеет вид
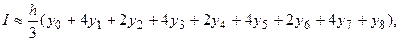
где  ,
,  .
.
Вычисления значения функции запишем в таблице 6:
Таблица 6

| 
| 
|
|
| 1.2
1.25
1.30
1.35
1.40
1.45
| 0.1211
0.1520
0.1782
0.2000
0.2176
0.2312
|
|
| 1.50
| 0.2410
|
Продолжение табл. 6
Следовательно,
 .
.
Задача №6
Задание. Получить численное решение дифференциального уравнения  , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию  на отрезке
на отрезке  с шагом
с шагом 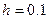 , методом Эйлера
, методом Эйлера
 ,
,  ,
,  .
.
Решение. Задача Коши для обыкновенного дифференциального уравнения, разрешенного относительно производной
 (1)
(1)
состоит в том, чтобы найти решение этого уравнения, удовлетворяющее начальному условию
 . (2)
. (2)
Простейшим численным методом решения задачи Коши является метод Эйлера, называемый иногда методом ломаных Эйлера.
Пользуясь тем, что в точке  известно и значение решения
известно и значение решения  и значение его производной
и значение его производной  , можно записать уравнение касательной к графику искомой функции
, можно записать уравнение касательной к графику искомой функции 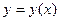 в точке
в точке  :
:
 . (3)
. (3)
При достаточно малом значении  ордината
ордината
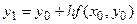
этой касательной, полученная подстановкой в правую часть (3) значения 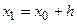 , по непрерывности должна мало отличаться от ординаты
, по непрерывности должна мало отличаться от ординаты  решения
решения  задачи (1)-(2). Следовательно, точка
задачи (1)-(2). Следовательно, точка  пересечения касательной с прямой
пересечения касательной с прямой 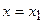 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
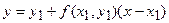 ,
,
которая уже приближенно отражает поведение касательной к  в точке
в точке 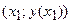 . Подставляя сюда
. Подставляя сюда  , получим приближение значения
, получим приближение значения  значением
значением
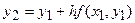
и т.д. Продолжая вычисления в соответствии с намеченной схемой, получим формулу Эйлера для решения задачи Коши (1) - (2)
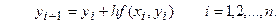 (4)
(4)
Геометрический смысл метода Эйлера заключается в том, что интегральная кривая 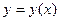 на каждом отрезке
на каждом отрезке  ,
,  , …,
, …,  заменяется отрезком касательной к интегральной кривой, проходящей через точки
заменяется отрезком касательной к интегральной кривой, проходящей через точки  , а интегральная кривая заменяется ломаной, проходящей через точки
, а интегральная кривая заменяется ломаной, проходящей через точки  ,
,  , …,
, …,  . Эта ломаная называется ломаной Эйлера.
. Эта ломаная называется ломаной Эйлера.
В нашем случае 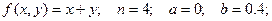
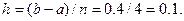
Находим последовательные значения аргумента:  ,
,  ,
, 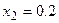 ,
, 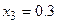 ,
,  . Вычислим соответствующие значения искомой функции:
. Вычислим соответствующие значения искомой функции:
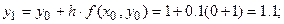
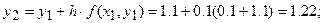
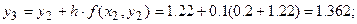
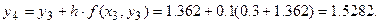
Результаты вычислений представим в таблице 7.
Таблица 7

|
| 0.1
| 0.2
| 0.3
| 0.4
|

|
| 1.1
| 1.22
| 1.362
| 1.5282
|
Задача №7
Задание. Найтичисленноерешение линейной краевой задачи для дифференциального уравнения 2-го порядка конечно-разностным методом, используя аппроксимацию производных второго порядка и шаг 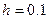 .
.
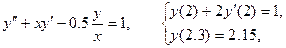
Решение. Метод конечных разностей.
Разбив отрезок  на части с шагом
на части с шагом 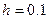 , получим четыре узловые точки с абсциссами
, получим четыре узловые точки с абсциссами 


 . Две точки
. Две точки  и
и  являются граничными, а две другие – внутренними. Данное уравнение во внутренних точках заменим конечно-разностным уравнением
являются граничными, а две другие – внутренними. Данное уравнение во внутренних точках заменим конечно-разностным уравнением
 (
( ).
).
Для краевых условий составим конечно-разностное уравнение в граничных точках
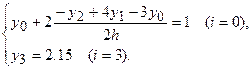
Данная задача сводится к решению системы уравнений
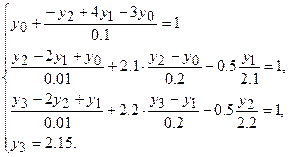
Выполнив преобразования, имеем
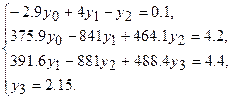
Подставив значение  в третье уравнение, получим для определения остальных неизвестных систему
в третье уравнение, получим для определения остальных неизвестных систему
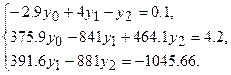
Решая эту систему уравнений, получим

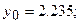

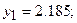

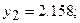

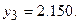

 = 0,
= 0, . Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займемся их приближенным вычислением с заданной точностью.
. Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займемся их приближенным вычислением с заданной точностью. значения разных знаков, т.е.
значения разных знаков, т.е.  , то внутри этого промежутка имеется хотя бы один корень уравнения.
, то внутри этого промежутка имеется хотя бы один корень уравнения. , пересекает эту ось, по меньшей мере в одной точке.
, пересекает эту ось, по меньшей мере в одной точке.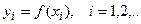 и, при этом о наличии корня на отрезке
и, при этом о наличии корня на отрезке  , судят по перемене знака функции на концах отрезка.
, судят по перемене знака функции на концах отрезка. .
. и построим графики функций
и построим графики функций  и
и  .
.
 и
и  .
. .
.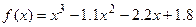 на отрезке
на отрезке  с шагом
с шагом
 меняет знак на концах отрезков
меняет знак на концах отрезков 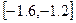 ,
,  ,
,  . Поэтому каждый из этих отрезков содержит хотя бы один корень. Поскольку
. Поэтому каждый из этих отрезков содержит хотя бы один корень. Поскольку  , то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности
, то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности  .
. сохраняют знак на отрезке
сохраняют знак на отрезке 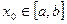 , удовлет-воряющего неравенству
, удовлет-воряющего неравенству  , можно построить последовательность
, можно построить последовательность  сходящуюся к единственному на
сходящуюся к единственному на  уравнения
уравнения  касательной, проведенной в некоторой точке кривой (рис. 2).
касательной, проведенной в некоторой точке кривой (рис. 2). , для которого
, для которого 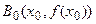 . В качестве первого приближения
. В качестве первого приближения  корня
корня  . Через точку
. Через точку  снова проведем касательную, абсцисса точки пересечения которой даст второе приближение
снова проведем касательную, абсцисса точки пересечения которой даст второе приближение  корня
корня 
 .Найдем производную данной функции
.Найдем производную данной функции  .
.


 . Уточним этот корень методом касательных. Так как
. Уточним этот корень методом касательных. Так как 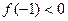 ,
, 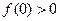 и
и  , то за начальное приближение принимаем
, то за начальное приближение принимаем  .
.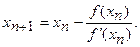

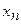



 .
.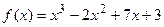 .
. . При этом должно выполняться условие
. При этом должно выполняться условие  для
для  . Функцию
. Функцию  будем искать из соотношения
будем искать из соотношения  , считая, что
, считая, что  , где
, где  число
число  имеет тот же знак, что и
имеет тот же знак, что и  в промежутке
в промежутке 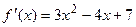 .
. , то можно взять
, то можно взять 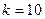 . Тогда
. Тогда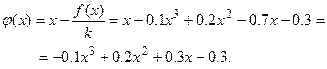
 , тогда
, тогда  . Вычисления располагаем в таблице 4.
. Вычисления располагаем в таблице 4.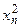


 .
.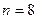 ; оценить погрешность результата, составив таблицу конечных разностей.
; оценить погрешность результата, составив таблицу конечных разностей. ; 2)
; 2)  .
. :
: .
. . При этом
. При этом  . Обозначим через
. Обозначим через  значение функции
значение функции  .
. , считать приближенно равной площади соответствующей трапеции, то для вычисления интеграла получаем формулу трапеций (рис. 3)
, считать приближенно равной площади соответствующей трапеции, то для вычисления интеграла получаем формулу трапеций (рис. 3)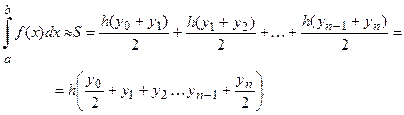

 . Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 4).
. Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 4).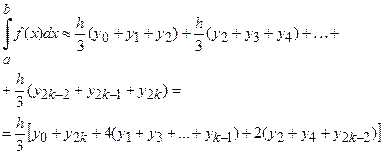

 (*)
(*) ;
;  ;
; 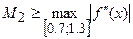 , где
, где  .
. ,
,  ;
; .
. , тогда неравенство (*) примет вид
, тогда неравенство (*) примет вид  , откуда
, откуда  , т.е.
, т.е.  ; возьмем
; возьмем  .
. ,
,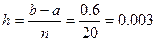 ;
;  ;
; 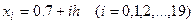 .
.


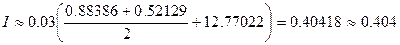 .
. .
.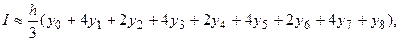
 ,
,  .
. .
. , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию  на отрезке
на отрезке 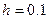 , методом Эйлера
, методом Эйлера ,
,  ,
,  .
. . (2)
. (2) известно и значение решения
известно и значение решения  , можно записать уравнение касательной к графику искомой функции
, можно записать уравнение касательной к графику искомой функции 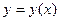 в точке
в точке  :
: . (3)
. (3) ордината
ордината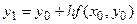
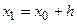 , по непрерывности должна мало отличаться от ординаты
, по непрерывности должна мало отличаться от ординаты  решения
решения  задачи (1)-(2). Следовательно, точка
задачи (1)-(2). Следовательно, точка  пересечения касательной с прямой
пересечения касательной с прямой 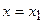 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую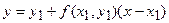 ,
,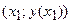 . Подставляя сюда
. Подставляя сюда  , получим приближение значения
, получим приближение значения  значением
значением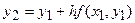
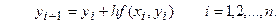 (4)
(4) ,
,  , …,
, …,  заменяется отрезком касательной к интегральной кривой, проходящей через точки
заменяется отрезком касательной к интегральной кривой, проходящей через точки  , а интегральная кривая заменяется ломаной, проходящей через точки
, а интегральная кривая заменяется ломаной, проходящей через точки  ,
,  , …,
, …,  . Эта ломаная называется ломаной Эйлера.
. Эта ломаная называется ломаной Эйлера.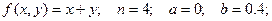
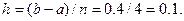
 ,
,  ,
, 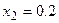 ,
, 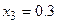 ,
,  . Вычислим соответствующие значения искомой функции:
. Вычислим соответствующие значения искомой функции: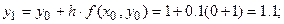
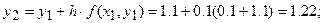
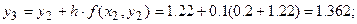
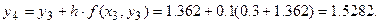


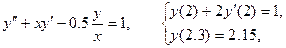
 на части с шагом
на части с шагом 


 . Две точки
. Две точки  и
и  (
( ).
).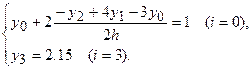
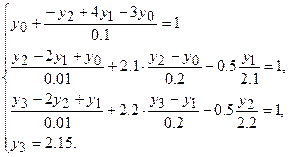
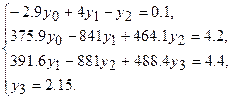
 в третье уравнение, получим для определения остальных неизвестных систему
в третье уравнение, получим для определения остальных неизвестных систему