Задача №1
Дана таблица значений функции  . Построить для этой функции интерполяционный многочлен Ньютона и с помощью его найти приближенное значение функции для заданного аргумента
. Построить для этой функции интерполяционный многочлен Ньютона и с помощью его найти приближенное значение функции для заданного аргумента  .
.
| X
| 3.50
| 3.55
| 3.60
| 3.65
| 3,70
| 
|
| Y
| 33.115
| 34.813
| 36.598
| 38.475
| 40.447
| 3.57
|
Решение. Часто приходится рассматривать функции  , заданные табличными значениями
, заданные табличными значениями 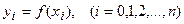 . Эти значения могут быть получены в результате расчета, эксперимента, опыта и т.д. Значения же функции в промежуточных точках неизвестны и их получение может быть связано с проведением сложных расчетов и экспериментов. В некоторых случаях даже при известной зависимости
. Эти значения могут быть получены в результате расчета, эксперимента, опыта и т.д. Значения же функции в промежуточных точках неизвестны и их получение может быть связано с проведением сложных расчетов и экспериментов. В некоторых случаях даже при известной зависимости  ее использование в практических расчетах затруднительно из-за ее громоздкости (содержит трудно вычисляемые выражения, сложные интегралы и т.д.).
ее использование в практических расчетах затруднительно из-за ее громоздкости (содержит трудно вычисляемые выражения, сложные интегралы и т.д.).
В связи с этим возникает задача о приближении (аппроксимации) функций: функцию  , заданную таблично или аналитически, аппроксимировать функцией
, заданную таблично или аналитически, аппроксимировать функцией  так, чтобы отклонение
так, чтобы отклонение  от
от  в заданной области было наименьшим. Функция
в заданной области было наименьшим. Функция  при этом называется аппроксимирующей.
при этом называется аппроксимирующей.
На практике очень важен случай аппроксимации функции многочленом
 . (1)
. (1)
При этом коэффициенты  подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции. В этом случае будем говорить о полиномиальной аппроксимации или кусочно-полиномиальной аппроксимации.
подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции. В этом случае будем говорить о полиномиальной аппроксимации или кусочно-полиномиальной аппроксимации.
Если приближение строится на заданном дискретном множестве точек  , то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и другие.
, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и другие.
При построении приближения на непрерывном множестве точек (например, на отрезке  ), аппроксимация называется непрерывной (или интегральной).
), аппроксимация называется непрерывной (или интегральной).
Одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции  строим многочлен (1), принимающий в заданных точках
строим многочлен (1), принимающий в заданных точках  те же значения
те же значения  , что и функция
, что и функция  , т.е.
, т.е.
 ,
,  . (2)
. (2)
При этом предполагается, что среди значений  нет одинаковых, т.е.
нет одинаковых, т.е.  при
при  .
.
Точки  называются узлами интерполяции, а многочлен
называются узлами интерполяции, а многочлен  - интерполяционным многочленом. Близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек.
- интерполяционным многочленом. Близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек.
Максимальная степень интерполяционного многочлена  , где
, где  -число узлов,
-число узлов,  -степень многочлена. В этом случае говорят о глобальной интерполяции, так как один многочлен
-степень многочлена. В этом случае говорят о глобальной интерполяции, так как один многочлен
 (3)
(3)
используется для интерполяции функции  на всем рассматриваемом интервале аргумента
на всем рассматриваемом интервале аргумента  . Коэффициенты
. Коэффициенты  многочлена (3) находятся из системы уравнений (2).
многочлена (3) находятся из системы уравнений (2).
Построим теперь интерполяционный многочлен, единый для всего отрезка  . Пусть для функции
. Пусть для функции  заданы
заданы  значения таблично заданной функции
значения таблично заданной функции  для равноотстоящих значений независимой переменной:
для равноотстоящих значений независимой переменной: 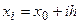 ,
,  , где
, где  шаг интерполяции.
шаг интерполяции.
Прежде чем получить такие формулы, рассмотрим элементы конечных разностей.
Составим разности значений заданной функции:
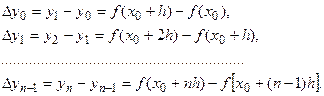
Эти разности называются конечными разностями первого порядка функции. Из них, в свою очередь, таким же образом можно получить  конечных разностей второго порядка, или вторых разностей:
конечных разностей второго порядка, или вторых разностей:
 Аналогично определяются разности III и IV и т.д. порядков. Разность порядка
Аналогично определяются разности III и IV и т.д. порядков. Разность порядка  определяется формулой:
определяется формулой:
 ,
,
где  и
и  .
.
В некоторых случаях требуется знать выражения конечных разностей непосредственно через значения функции. Для нескольких первых порядков разностей их можно получить непосредственной подстановкой
 ;
;
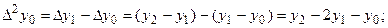

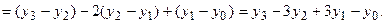
Аналогично для любого  можно записать:
можно записать:
 .
.
Такую же формулу можно записать и для значения разности в узле  :
:
 .
.
Для функции  , заданной таблицей своих значений
, заданной таблицей своих значений  в узлах
в узлах  , конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции. Обычно используют горизонтальную таблицу или диагональную таблицу конечных разностей
, конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции. Обычно используют горизонтальную таблицу или диагональную таблицу конечных разностей
Интерполяционный многочлен Ньютона для заданной функции имеет вид
 (4)
(4)
где  .
.
Интерполяционную формулу (4) обычно используют для вычисления значений функции в левой половине отрезка. Дело в том, что разности  вычисляются через значения функции
вычисляются через значения функции  , причем
, причем  . Поэтому при больших значениях
. Поэтому при больших значениях  мы не можем вычислить разности высших порядков
мы не можем вычислить разности высших порядков  . Например, при
. Например, при 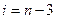 в (4) можно учесть только
в (4) можно учесть только  ,
,  и
и  .
.
Составим таблицу конечных разностей для заданных значений (таблица 1):
Таблица 1

| 
| 
| 
| 
|
| 3.50
3.55
3.60
3.65
3.70
| 33.115
34.813
36.598
38.475
40.447
| 1.698
1.785
1.877
1.972
------
| 0.087
0.092
0.095
------
------
| 0.005
0.003
------
------
------
|
При составлении таблицы конечных разностей ограничиваемся разностями третьего порядка, так как они практически постоянны. Поэтому в формуле Ньютона полагаем  . Приняв
. Приняв  ,
,  , будем иметь:
, будем иметь:
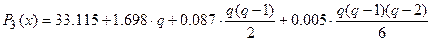
или
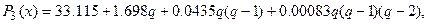
где 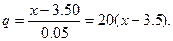
Подставим в выражение для  вместо
вместо  значение
значение  .
.
Получим 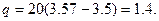
Тогда,  Следовательно,
Следовательно, 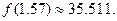
Задача №2
Задание. Дана таблица значений функции  . Используя метод наименьших квадратов, подобрать для заданных значений
. Используя метод наименьших квадратов, подобрать для заданных значений  и
и 
1) линейную функцию  ;
;
2) квадратичную функцию  .
.
Построить графики этих функций.
| X
| 0.5
| 1.0
| 1.5
| 2.0
| 2.5
| 3.0
|
| Y
| 0.31
| 0.82
| 1.29
| 1.85
| 2.51
| 3.02
|
Решение. Пусть для неизвестной функции  в точках
в точках  экспериментальным путем получены значения
экспериментальным путем получены значения  . Интерполяция позволяет аппроксимировать таблично заданную функцию
. Интерполяция позволяет аппроксимировать таблично заданную функцию  с помощью более простой функции
с помощью более простой функции  . При этом требуется выполнение в узлах интерполяции
. При этом требуется выполнение в узлах интерполяции  равенства
равенства  (
( ). В ряде случаев выполнение этого условия затруднительно или даже нецелесообразно. При большом числе узлов интерполяции степень интерполирующего многочлена получается высокой. Поэтому точность такой аппроксимации гарантирована лишь в небольшом интервале порядка несколько шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. В практических приложениях желательно иметь единую приближенную формулу
). В ряде случаев выполнение этого условия затруднительно или даже нецелесообразно. При большом числе узлов интерполяции степень интерполирующего многочлена получается высокой. Поэтому точность такой аппроксимации гарантирована лишь в небольшом интервале порядка несколько шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. В практических приложениях желательно иметь единую приближенную формулу  (
( ), пригодную для большего отрезка
), пригодную для большего отрезка  . При этом точность приближения может оцениваться по разному. В основу обычно берется рассмотренное отклонение
. При этом точность приближения может оцениваться по разному. В основу обычно берется рассмотренное отклонение
 (
( ).
).
В связи с этим возникает задача приближения таблично заданной функции  многочленом
многочленом  , который имеет не слишком высокую степень
, который имеет не слишком высокую степень  и дает в некотором смысле разумную точность аппроксимации.
и дает в некотором смысле разумную точность аппроксимации.
Для решения этой задачи воспользуемся методом наименьших квадратов. В методе наименьших квадратов за меру отклонения многочлена 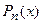 от функции
от функции  принимается их среднее квадратичное отклонение
принимается их среднее квадратичное отклонение
 .
.
Задача состоит в том, чтобы в аппроксимирующем многочлене  подобрать коэффициенты
подобрать коэффициенты  так, чтобы минимизировать
так, чтобы минимизировать  Так как коэффициенты
Так как коэффициенты 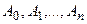 выступают в роли независимых переменных функции
выступают в роли независимых переменных функции  , то необходимым условием минимума является равенство нулю всех частных производных
, то необходимым условием минимума является равенство нулю всех частных производных  ,
, 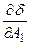 , …,
, …,  . Приравнивая нулю эти частные производные получим систему уравнений
. Приравнивая нулю эти частные производные получим систему уравнений
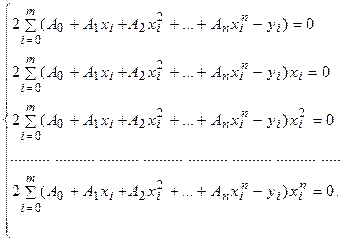
После преобразования система принимает вид

Определитель этой системы отличен от нуля, поэтому эта система имеет единственное решение 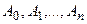 .
.
1) Аппроксимируем таблично заданную функцию  линейной
линейной  .
.
Составим систему для определения 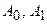
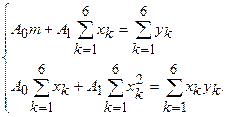
Предварительно вычисляем  ,
,  ,
,  ,
,  Следовательно,
Следовательно, 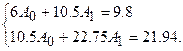
Решая эту систему, находим 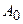 и
и  :
:  ,
,  .
.
Искомый многочлен  .
.
2) Аппроксимируем таблично заданную функцию  квадратичной функцией
квадратичной функцией  .
.
Составим систему для определения 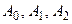
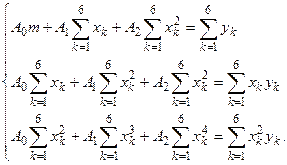
Предварительно вычисляем
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,  ,
,
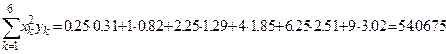
Получим систему уравнений вида
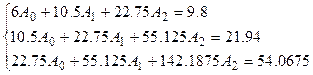
Решая эту систему, находим  ,
,  и
и  :
:  ,
,  ,
,  .
.
Искомый многочлен 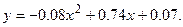
Задача №3
Задание. Получить приближенное решение системы методом простой итерации с точностью 0.01.
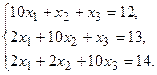
Решение. Пусть дана система линейных уравнений
 (1)
(1)
Введя в рассмотрение матрицы
 ,
,  ,
,  .
.
систему (1) можно записать в виде матричного уравнения
 . (2)
. (2)
Предполагая, что диагональные коэффициенты 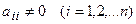 , разрешим первое уравнение системы (1) относительно
, разрешим первое уравнение системы (1) относительно  , второе – относительно
, второе – относительно  и т.д. Тогда получим эквивалентную систему
и т.д. Тогда получим эквивалентную систему
 (3)
(3)
где 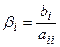 ,
,  при
при 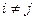
и  при
при  Введя матрицы
Введя матрицы
 ,
,  ,
,
систему (3) можем записать в матричной форме
 . (4)
. (4)
Для решения системы (4) применим метод последовательных приближений. За начальное приближение принимаем, например, столбец свободных членов  .
.
Далее, последовательно строим матрицы-столбцы
 ,
,  ,….,
,….,  , …
, …
Если последовательность приближений  имеет предел
имеет предел
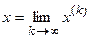 ,
,
то этот предел является решением системы (4) и, cледовательно, решением равносильной системы (1).
Для того чтобы процесс итераций сходился к единственному решению этой системы, независимо от выбора начального приближения, необходимо выполнение для приведенной системы (3) по меньшей мере одного из условий (достаточное условие сходимости метода итераций)
 или
или
 .
.
Приведем заданную систему уравнений к виду (3)

В качестве начального приближения возьмем систему чисел  ;
;  ;
;  .
.
После первого шага получим:
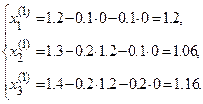
После второго: 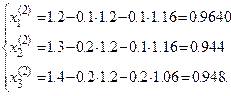
Дальнейшие вычисления располагаем в таблице 2:
Таблица 2

| 
| 
| 
|
|
| 1.2000
1.2000
0.9640
1.0098
0.9975
1.0007
0.9998
| 0.0000
1.0600
0.9440 1.0104
0.9966
1.0009
0.9997
| 0.0000
1.1600
0.9480
1.0144
0.9960
1.0012
0.9997
|
Точное решение ( ) практически достигается на 6-ой итерации.
) практически достигается на 6-ой итерации.
Задача №4
Задание. Отделить корни и найти приближенное решение заданного уравнения с точностью  методом Ньютона (1) и методом итераций (2).
методом Ньютона (1) и методом итераций (2).
1)  ; 2)
; 2)  .
.

 . Построить для этой функции интерполяционный многочлен Ньютона и с помощью его найти приближенное значение функции для заданного аргумента
. Построить для этой функции интерполяционный многочлен Ньютона и с помощью его найти приближенное значение функции для заданного аргумента  .
.
 , заданные табличными значениями
, заданные табличными значениями 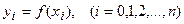 . Эти значения могут быть получены в результате расчета, эксперимента, опыта и т.д. Значения же функции в промежуточных точках неизвестны и их получение может быть связано с проведением сложных расчетов и экспериментов. В некоторых случаях даже при известной зависимости
. Эти значения могут быть получены в результате расчета, эксперимента, опыта и т.д. Значения же функции в промежуточных точках неизвестны и их получение может быть связано с проведением сложных расчетов и экспериментов. В некоторых случаях даже при известной зависимости  ее использование в практических расчетах затруднительно из-за ее громоздкости (содержит трудно вычисляемые выражения, сложные интегралы и т.д.).
ее использование в практических расчетах затруднительно из-за ее громоздкости (содержит трудно вычисляемые выражения, сложные интегралы и т.д.). так, чтобы отклонение
так, чтобы отклонение  . (1)
. (1) подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции. В этом случае будем говорить о полиномиальной аппроксимации или кусочно-полиномиальной аппроксимации.
подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции. В этом случае будем говорить о полиномиальной аппроксимации или кусочно-полиномиальной аппроксимации. , то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и другие.
, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и другие. ), аппроксимация называется непрерывной (или интегральной).
), аппроксимация называется непрерывной (или интегральной). те же значения
те же значения  , что и функция
, что и функция  ,
,  . (2)
. (2) при
при  .
. , где
, где  -число узлов,
-число узлов,  -степень многочлена. В этом случае говорят о глобальной интерполяции, так как один многочлен
-степень многочлена. В этом случае говорят о глобальной интерполяции, так как один многочлен (3)
(3) значения таблично заданной функции
значения таблично заданной функции  для равноотстоящих значений независимой переменной:
для равноотстоящих значений независимой переменной: 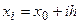 ,
,  , где
, где  шаг интерполяции.
шаг интерполяции.



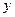




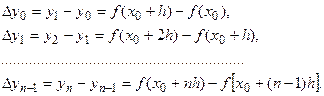
 конечных разностей второго порядка, или вторых разностей:
конечных разностей второго порядка, или вторых разностей: Аналогично определяются разности III и IV и т.д. порядков. Разность порядка
Аналогично определяются разности III и IV и т.д. порядков. Разность порядка  определяется формулой:
определяется формулой: ,
, и
и  .
. ;
;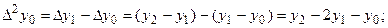

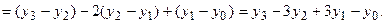
 .
. :
: .
. в узлах
в узлах  , конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции. Обычно используют горизонтальную таблицу или диагональную таблицу конечных разностей
, конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции. Обычно используют горизонтальную таблицу или диагональную таблицу конечных разностей (4)
(4) .
. вычисляются через значения функции
вычисляются через значения функции  , причем
, причем  . Поэтому при больших значениях
. Поэтому при больших значениях  мы не можем вычислить разности высших порядков
мы не можем вычислить разности высших порядков  . Например, при
. Например, при 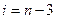 в (4) можно учесть только
в (4) можно учесть только  ,
,  и
и  .
.




 . Приняв
. Приняв  ,
,  , будем иметь:
, будем иметь: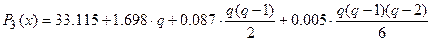
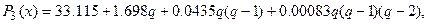
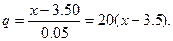
 вместо
вместо 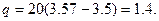
 Следовательно,
Следовательно, 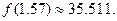
 ;
; .
. экспериментальным путем получены значения
экспериментальным путем получены значения  . Интерполяция позволяет аппроксимировать таблично заданную функцию
. Интерполяция позволяет аппроксимировать таблично заданную функцию  . При этом требуется выполнение в узлах интерполяции
. При этом требуется выполнение в узлах интерполяции  равенства
равенства  (
( ). В ряде случаев выполнение этого условия затруднительно или даже нецелесообразно. При большом числе узлов интерполяции степень интерполирующего многочлена получается высокой. Поэтому точность такой аппроксимации гарантирована лишь в небольшом интервале порядка несколько шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. В практических приложениях желательно иметь единую приближенную формулу
). В ряде случаев выполнение этого условия затруднительно или даже нецелесообразно. При большом числе узлов интерполяции степень интерполирующего многочлена получается высокой. Поэтому точность такой аппроксимации гарантирована лишь в небольшом интервале порядка несколько шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. В практических приложениях желательно иметь единую приближенную формулу  (
( (
( , который имеет не слишком высокую степень
, который имеет не слишком высокую степень  и дает в некотором смысле разумную точность аппроксимации.
и дает в некотором смысле разумную точность аппроксимации.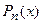 от функции
от функции  .
. подобрать коэффициенты
подобрать коэффициенты  так, чтобы минимизировать
так, чтобы минимизировать  Так как коэффициенты
Так как коэффициенты 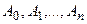 выступают в роли независимых переменных функции
выступают в роли независимых переменных функции  , то необходимым условием минимума является равенство нулю всех частных производных
, то необходимым условием минимума является равенство нулю всех частных производных  ,
, 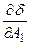 , …,
, …,  . Приравнивая нулю эти частные производные получим систему уравнений
. Приравнивая нулю эти частные производные получим систему уравнений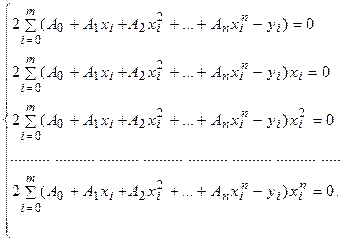

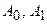
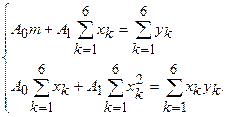
 ,
,  ,
,  ,
,  Следовательно,
Следовательно, 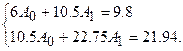
 и
и  :
:  ,
,  .
. .
. .
.
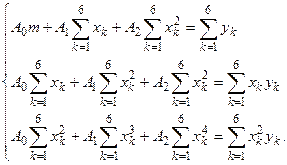
 ,
, ,
, ,
,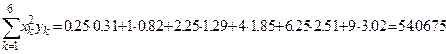
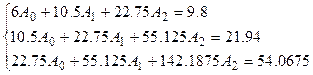
 ,
,  и
и  :
:  ,
,  ,
,  .
.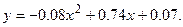
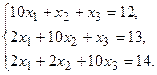
 (1)
(1) ,
,  ,
,  .
. . (2)
. (2)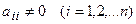 , разрешим первое уравнение системы (1) относительно
, разрешим первое уравнение системы (1) относительно  , второе – относительно
, второе – относительно  и т.д. Тогда получим эквивалентную систему
и т.д. Тогда получим эквивалентную систему (3)
(3)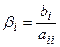 ,
,  при
при 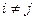
 при
при  Введя матрицы
Введя матрицы ,
,  ,
, . (4)
. (4) .
. ,
,  ,….,
,….,  , …
, … имеет предел
имеет предел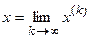 ,
, или
или .
.
 ;
;  ;
;  .
.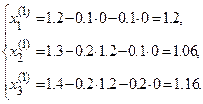
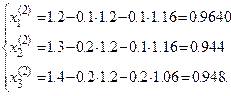


 ) практически достигается на 6-ой итерации.
) практически достигается на 6-ой итерации. методом Ньютона (1) и методом итераций (2).
методом Ньютона (1) и методом итераций (2). ; 2)
; 2)  .
.


