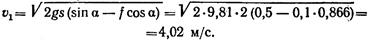Решение. Так как в число данных и искомых величин входят действующие силы (постоянные по величине и направлению)
Так как в число данных и искомых величин входят действующие силы (постоянные по величине и направлению), время движения, начальная и конечная скорости, то применяем теорему об изменении количества движения точки. Силы, действующие на точку в произвольном положении, показаны на рис. 1.67 Вычисляем проекции на ось х импульсов сил, действующих на тело:
(так как силы О и N перпендикулярны к оси х),
Составляем уравнение изменения количества движения
откуда
Пример 5. По наклонной плоскости с углом α; = 30° опускается без начальной скорости тяжелое тело; коэффициент трения равен 0,1. Какую скорость будет иметь тело, пройдя 2 м от начала движения?
Так как в число данных и искомых величин входят действующие силы (постоянные по величине и направлению), перемещение точки, начальная и конечная скорости, то применим теорему об изменении кинетической энергии точки. Силы, действующие на тело в произвольном положении, показаны на рис. 1.68 (G — сила тяжести тела, N — реакция плоскости, Ттр — сила трения). Вычислим работы сил, действующих на тело:
(так как N и G1 перпендикулярны к перемещению точки их приложения). Составляем уравнение изменения кинетической энергии:
Так как тело опускается без начальной скорости, то v о = 0, тогда
откуда
Пример 6. Поезд массой т — 3-106 кг движется по прямолинейному участку пути со скоростью 20 м/с. Тормозной путь составляет 500 м. Определить время и силу торможения, считая ее постоянной.
|
— сила тяжести тела, N — реакция поверхности, Р — движущая сила).
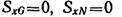
Решение
