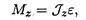Основное уравнение динамики при поступательном движении телаДля определения движения тела (системы материальных точек) можно использовать второй закон динамики
где т — суммарная масса тела; ас — ускорение центра масс тела. В поле земного притяжения центр масс совпадает с центром тяжести.
Пусть твердое тело под действием внешних сил вращается вокруг оси Oz с угловой скоростью ω (рис. 17.3). Рассматривая твердое тело как механическую систему, разобьем ее на множество материальных точек с массами Δmk. Каждая точка движется по окружности радиуса rk c касательным ускорением аkt = εrk и нормальным ускорением
Используем для каждой точки принцип Даламбера и приложим силы инерции:
Система сил, действующих на точку, по принципу Даламбера, находится в равновесии. Поэтому алгебраическая сумма моментов относительно оси вращения должна быть равна нулю:
где Mz — момент внешних сил. Моменты нормальных сил инерции Fинkn равны нулю, т. к. силы пересекают ось z. Силы, направленные по касательной к окружности, равны
где ε — общая величина, угловое ускорение тела. Подставив значение силы в формулу для определения моментов, получим
Величина
называется моментом инерции тела относительно оси вращения и обозначается
В результате получим выражение основного уравнения динамики вращающего тела:
где Mz — сумма моментов внешних сил относительно оси; ε — угловое ускорение тела.
Момент инерции тела в этом выражении определяет меру инертности тела при вращении. По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ [Jz\ = [тг2] = кг-м2. Видно, что значение момента инерции зависит от распределения массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от оси вращения. Для увеличения момента инерции используют колеса со спицами и отверстиями.
|
Основное уравнение динамики вращающегося тела
где ε — угловое ускорение.
