Решение
1. Ускорение точки: a = v' = S"; v = S' = 0,96 t + 0,2; a = v' = 0,96 м/с2. 2. Действующая сила согласно основному закону динамики F = ma; F = 5 * 0,96 = 4,8 Н.
Пример 2. Тело массой т = 2 кг движется по гладкой горизонтальной поверхности согласно уравнению S = 2t3 (S — в метрах, (t — в секундах). Определить силу Р в конце второй секунды после начала движения.
Тело движется по прямой. Следовательно, и сила, действующая на точку, направлена по этой же прямой. Силы, действующие на тело, показаны на рис. 1.57 (т g — сила тяжести тела, N — реакция поверхности, Р — искомая сила). Очевидно, что
Определим ускорение тела в конце второй секунды. Как известно,
Продифференцировав дважды уравнение движения, получим
Ускорение тела в конце второй секунды
Тогда
Пример 3. К двум материальным точкам массой m1 = 2 кг и m2 = 5 кг приложены одинаковые силы. Сравнить величины ускорений. Решение Согласно третьей аксиоме динамики ускорения обратно пропорциональны массам: a1 /a2 = m2/m1 = 5/2 = 2,5 a1 = 2,5 a2
Решение Й вариант. 1. Определяем суммарную силу, действующую на точку:
2. Определяем ускорение, сообщенное точке: a∑ = 28/7 = 4 м/с2 Й вариант. Определяем ускорения от каждой из сил системы (рис. 13.5, б): а1 = 10/7 = 1,43 м/с2, а2 = 15/7 = 2,14 м/с2; а3 = 20/7 = 2,86 м/с2. 2. Определяем суммарное ускорение:
|

 Решение
Решение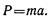

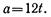
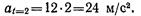

 Пример 4. На материальную точку действует система сил (рис. 13.5). Определить числовое значение ускорения, полученного материальной точкой m = 7 кг. Остальные данные представлены на чертеже.
Пример 4. На материальную точку действует система сил (рис. 13.5). Определить числовое значение ускорения, полученного материальной точкой m = 7 кг. Остальные данные представлены на чертеже.
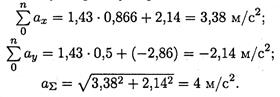
 Пример 4. Материальная точка, сила тяжести которой G = 100 Н, движется по прямолинейной гладкой поверхности (рис. 1.58) с ускорением а = 1,5 м/с2. Определить силу Р, вызывающую движение, пренебрегая силами сопротивления.
Пример 4. Материальная точка, сила тяжести которой G = 100 Н, движется по прямолинейной гладкой поверхности (рис. 1.58) с ускорением а = 1,5 м/с2. Определить силу Р, вызывающую движение, пренебрегая силами сопротивления.


