Решение. По заданному закону движения точки О определяем ее скорость в момент времени t = 2 с:
По заданному закону движения точки О определяем ее скорость в момент времени t = 2 с:
при t = 2 с v 0 = 9 м/с. Цилиндр совершает плоскопараллельное движение. Мгновенный центр вращения находится в точке Р. Поэтому
Отсюда мгновенная угловая скорость вращения цилиндра
Найдем расстояния от мгновенного центра скоростей Р до заданных точек:
Для определения расстояния РН рассмотрим прямоугольные треугольники НКО и РКН. Из треугольника НКО имеем
Теперь определим величины скоростей заданных точек:
Вектора скоростей показаны на рис. 1.52. Пример 8. В механизме грохота (рис. 1.53, а) кривошипы O1А и O2В связаны звеном АВ. Размеры всех звеньев одинаковы: O1А = O2В = АВ = 40 см. Кривошип O1A равномерно вращается вокруг оси Ох с частотой п о = 60 об/мин. Определить угловую скорость звена АВ и скорость точки В для двух положений грохота: 1) когда кривошип O1A занимает горизонтальное положение, 2) когда кривошип O2В занимает горизонтальное положение.
Вычислим скорость точки А ведущего кривошипа:
Рассмотрим теперь последовательно заданные положения механизма. 1-е положение (рис. 1.53, б). При заданных размерах звеньев угол АВО2 = 90°. Определим мгновенный центр вращения звена АВ. Нам известны направления скоростей двух его точек: vA и vB. Мгновенный центр скоростей лежит на пересечении перпендикуляров к направлениям скоростей vA и vB, т. е. в точке О2. Найдем мгновенную угловую скорость вращения звена АВ:
откуда
Определяем скорость точки В: 2-е положение (рис. 1.53, в). Мгновенный центр скоростей в этом положении находится в точке Ov. Мгновенная угловая скорость вращения звена АВ оказывается равной угловой скорости ведущего кривошипа механизма:
Определяем скорость точки В:
Пример 9. Железнодорожный вагон движется по горизонтальному участку с ускорением а0 = — 1,6 м/с2, имея в данный момент скорость v 0 = 1 м/с. Найти ускорения точек вагонного колеса, лежащих на концах горизонтального и вертикального диаметров (рис. 1.54).
|




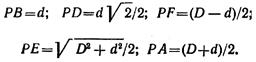
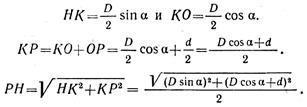

 Решение
Решение








