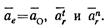Решение. Движение центра колеса О примем за переносное ае = а0

 

Движение центра колеса О примем за переносное а_е = а₀. Относительное движение является враща­тельным относительно выбранного полюса О. Найдем угловую скорость и угловое ускорение относительного движения.

Составим выражение скорости точки О в произвольный момент времени:

Рассматривая движение точки О относительно мгно­венного центра скоростей, который совпадает с точкой Р, найдем угловую скорость вращения колеса:

ω = v₀/OP = v₀/R = 1/0,4 = 2,5 рад/с.

Как известно, v = ωR. Продифференцируем полученное уравнение по времени:

Следовательно, a_t = Rε;.

В рассматриваемом примере a_t — касательное ускоре­ние точки О в поступательном движении, т. е. a_t = — a₀ (движение замедленное), ε; — угловое ускорение колеса во вращательном движении вокруг точки О.

Тогда

Поскольку все исследуемые точки А, В, Р и С нахо­дятся на одинаковом расстоянии от центра колеса, то относительные касательные и нормальные ускорения их по величине соответственно одинаковы и определяются по формулам:

На рис. 1.54 в каждой точке построены три состав­ляющих ускорения:

Два из трех составляющих векторов для каждой точ­ки направлены по одной прямой и складываются алгебраи­чески. Векторные построения, выполненные на рис. 1.54 около точек А, В и Р, позволяют найти величины и на­правления их абсолютных ускорений:

 

 

Контрольные вопросы и задания

1. Какое движение называют сложным?
2. Какие движения твердого тела называют простыми?
3. Какие системы координат выбирают при определении скоро­стей твердых тел при сложном движении?
4. Какое движение считают переносным, а какое — относитель­ным?
5. Сформулируйте теорему сложения скоростей.
6. Какое движение называют плоским?
7. Какие способы применяют для определения скоростей точек тела при плоскопараллельном движении?
8. Что такое мгновенный центр скоростей, как его определяют и для чего используют?
9. Ответьте на вопросы тестового задания.

Темы 1.10, 1.11. Кинематика. Сложное движение точки. Сложное движение твердого тела