Задачи. 1. Найти положение центра тяжести площади листа.
1. Найти положение центра тяжести площади листа.
2. Найти центр тяжести поперечного сечения вала диаметром 12 см, в котором высверлено отверстие диаметром 2 см.
3. Определить положение центра тяжести сечения, составленного из равнобокого уголка 100
Для заметок.
КИНЕМАТИКА Тема 1.7. Основные понятия кинематики. 1.7.1. Предмет кинематики. 1.7.2. Траектория. Путь. Перемещение. 1.7.3. Способы задания движения точки. 1.7.4. Скорость точки. 1.7.5. Ускорение точки. 1.7.1. Кинематикой называется раздел теоретической механики, изучающий движение тел лишь с геометрической стороны, вне зависимости от факторов, обуславливающих тот или иной характер этого движения. Кинематика целиком основывается на аксиомах и положениях геометрии, но отличается от неё тем, что кроме пространства, проходимого движущимся телом, она рассматривает ещё и время, за которое совершается движение. Всякое механическое движение материального тела можно наблюдать и изучать лишь по отношению к каким-либо другим телам. Твёрдое тело, по отношению к которому с помощью системы координат определяется положение других тел в разные моменты времени, называется телом отсчёта. Тело отсчёта, связанные с ним система координат и часы называются системой отсчёта. Пространство в механике рассматривается как трёхмерное евклидово пространство. Все измерения в нём производятся на основании методов евклидовой геометрии. За единицу длины при измерении расстояний принимается один метр. Время в механике считается универсальным, т.е. протекающим одинаково во всех системах отсчёта. За единицу времени принимается одна секунда. Время является скалярной непрерывно меняющейся величиной. В задачах кинематики его принимают за независимое переменное. Все другие величины (расстояния, скорости и т.д.) рассматриваются как функции времени. По характеру рассматриваемых материальных объектов кинематику делят на кинематику точки и кинематику абсолютно твёрдого тела. При движении тела все отдельные его точки в общем случае совершают различные движения. Поэтому кинематику начнём изучать с рассмотрения движения точки, т.е. с кинематики точки.
1.7.2. В процессе своего движения точка последовательно занимает различные положения относительно принятой системы отсчета, причем эти положения непрерывно следуют одно за другим.
Движение точки называется прямолинейным, если ее траектория—прямая линия, и криволинейным, если ее траектория—кривая линия. В зависимости от формы кривой криволинейное движение в свою очередь может быть различным: круговым (когда траектория точки — окружность или ее дуга), эллиптическим (когда траектория точки—эллипс), винтовым (когда траектория точки — винтовая линия) и т. д. Форма траектории зависит, конечно, от выбора системы отсчета. Например, камень, брошенный вертикально вверх с тележки, движущейся поступательно, прямолинейно и равномерно, будет относительно наблюдателя, находящегося на тележке, двигаться прямолинейно, а относительно наблюдателя, стоящего на той поверхности., по которой движется тележка, - по параболе. Всякая классификация движений носит относительный характер и имеет смысл только тогда, когда эти движения рассматриваются относительно одной и той же системы отсчета. Расстояние, пройденное телом вдоль траектории движения, называют пройденным путем (рис. 1.7.1.). Путь обозначают буквой Если известны траектория движения тела, его начальное положение и пройденный им путь, то можно определить положение тела в тот или иной момент времени. Если траектория не известна, то положение тела, зная пройденный им путь, определить нельзя, так как этот путь мог быть пройден телом в любом направлении. В этом случае надо знать направление движения тела и расстояние, пройденное в этом направлении. Пусть в начальный момент времени тело занимало положение А, а в момент времени t положение В (рис. 1.7.1.). Направление от А к В и есть направление движения тела. Перемещением тела называют направленный отрезок прямой (вектор), соединяющий начальное положение тела с его конечным положением.Вданном случае — это вектор Перемещение — величина векторная. Она имеет определенное числовое значение и направление. Перемещение – величина относительная. Следует иметь в виду, что перемещение тела может не совпадать с траекторией, а модуль перемещения с пройденным путем. Например, поезд отправился из Москвы в Санкт-Петербург и вернулся обратно. Расстояние между этими городами 650 км. Перемещение поезда в данном случае равно нулю, а его путь — 1300 км. Если точка в равные, произвольно взятые, промежутки времени проходит пути одинаковой длины, то движение точки называется равномерным, в противном случае движение точки называется неравномерным или переменным. Движение точки характеризуется признаками, устанавливаемыми каждой из двух данных выше классификаций. Как прямолинейное, так и криволинейное движение точки может одновременно быть или равномерным, или неравномерным (переменным) движением.
1.7.3. Движение тела считается известным тогда, когда мы имеем возможность определить его положение относительно выбранной системы отсчёта в каждый момент. Рассмотрим два способа задания движения точки: естественный и координатный.
В качестве системы отсчёта в дальнейшем используется прямоугольная декартова система координат Oxyz, которая условно принимается за неподвижную. Задать движение точки в координатной форме – это значит задать координаты этой точки как функции времени:
Уравнения (1.7.1.) называются уравнениями движения точки. Уравнения движения (1.7.1.) точки в прямоугольных координатах, определяя положение движущейся точки в любой момент времени, определяют тем самым и её траекторию.
1.7.4. Скоростью точки называется вектор, определяющий в каждый данный момент быстроту и направление движения точки.
. Направление вектора средней скорости совпадает с направлением вектора
Мгновенная скорость
Таким образом, модуль мгновенной скорости При неравномерном движении модуль мгновенной скорости с течением времени изменяется.
1.7.5. В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физическая величина, характеризующая быстроту изменения скорости по модулю и направлению, называется ускорением. Рассмотрим плоское движение, т.е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор
. Мгновенным ускорением
Таким образом, ускорение Разложим вектор
|

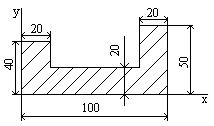
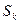 каждой части, мм
каждой части, мм 


 100
100 
 Геометрическое место положений движущейся точки в рассматриваемой системе отсчета называется траекторией этой точки (рис. 1.7.1.).
Геометрическое место положений движущейся точки в рассматриваемой системе отсчета называется траекторией этой точки (рис. 1.7.1.). или
или 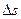 . Основной единицей пути является 1 метр (м).
. Основной единицей пути является 1 метр (м). (рис. 1.7.1.).
(рис. 1.7.1.). Естественный способ задания движения точки. Задать движение точки естественным способом – это значит: а) задать траекторию АВ движения точки в некоторой системе отсчёта Oxyz; б) на траектории выбрать начало отсчёта О и положительное направление отсчёта расстояний; в) указать закон движения точки М по данной траектории в виде уравнения
Естественный способ задания движения точки. Задать движение точки естественным способом – это значит: а) задать траекторию АВ движения точки в некоторой системе отсчёта Oxyz; б) на траектории выбрать начало отсчёта О и положительное направление отсчёта расстояний; в) указать закон движения точки М по данной траектории в виде уравнения  , где s – расстояние точки М, измеряемое по дуге ОМ, от начала отсчёта в данный момент времени t (рис. 1.7.2.).
, где s – расстояние точки М, измеряемое по дуге ОМ, от начала отсчёта в данный момент времени t (рис. 1.7.2.). Координатный способ задания движения. Положение точки в пространстве трёх измерений можно однозначно определить, задав три её координаты в некоторой системе отсчёта (рис. 1.7.3.).
Координатный способ задания движения. Положение точки в пространстве трёх измерений можно однозначно определить, задав три её координаты в некоторой системе отсчёта (рис. 1.7.3.). (1.7.1.)
(1.7.1.) Пусть материальная точка движется по какой-либо криволинейной траектории (рис. 1.7.4.) так, что в течении малого промежутка времени
Пусть материальная точка движется по какой-либо криволинейной траектории (рис. 1.7.4.) так, что в течении малого промежутка времени 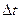 точка пройдёт путь
точка пройдёт путь  . Вектором средней скорости
. Вектором средней скорости  называется отношение перемещения
называется отношение перемещения  . При неограниченном уменьшении
. При неограниченном уменьшении 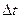 средняя скорость стремится к предельному значению, которое называется мгновенной скоростью
средняя скорость стремится к предельному значению, которое называется мгновенной скоростью  :
: . (1.7.2.)
. (1.7.2.)
 всё больше будет приближаться к
всё больше будет приближаться к  , поэтому модуль мгновенной скорости
, поэтому модуль мгновенной скорости (1.7.3.)
(1.7.3.)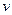 равен первой производной пути по времени.
равен первой производной пути по времени. . За промежуток времени
. За промежуток времени  (рис. 1.7.5.). Перенесём вектор
(рис. 1.7.5.). Перенесём вектор 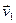 в точку А и найдём
в точку А и найдём  .
. Средним ускорением
Средним ускорением  нераномерного движения в интервале от
нераномерного движения в интервале от  называется векторная величина, равная отношению изменения скорости
называется векторная величина, равная отношению изменения скорости 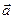 материальнойточки в момент времени
материальнойточки в момент времени  . (1.7.4.)
. (1.7.4.) , по модулю равный
, по модулю равный  , равный
, равный  , определяет изменение скорости за время
, определяет изменение скорости за время 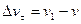 . Вторая же составляющая
. Вторая же составляющая  вектора
вектора 


