Тема 1.6. Центр тяжести тела.
1.6.1.Сложение параллельных сил. Центр параллельных сил. 1.6.2. Понятие о центре тяжести тела. 1.6.3. Координаты центра тяжести тела. 1.6.4. Центр тяжести симметричного тела. 1.6.5. Определение положения центра тяжести фигур и тел сложной формы. 1.6.1. Равнодействующая двух параллельных сил, направленных в одну сторону (рис. 1.6.1.), им параллельна, направлена в ту же сторону и равна по модулю их сумме:
линия действия равнодействующей лежит между линиями действия составляющих сил на расстояниях от них, обратно пропорциональных модулям этих сил:
Равнодействующая двух не равных по модулю параллельных сил, направленных в противоположные стороны (рис. 1.6.2.), им параллельна, направлена в сторону большей силы и равна по модулю их разности:
линия действия равнодействующей лежит за большей силой на расстояниях от линий действия составляющих сил, обратно пропорциональных модулям этих сил:
Зная правила сложения двух параллельных сил, нетрудно путём последовательного сложения найти равнодействующую и для любой системы параллельных сил
Остаётся определить положение точки С, через которую проходит линия действия равнодействующей. За точку приложения равнодействующей. Конечно, может быть взята любая точка, лежащая на линии её действия, но оказывается, что только одна из них, именно точка С, определённая путём последовательного сложения сил, обладает особым, весьма важным свойством: если мы повернём все данные силы вокруг их точек приложения на одинаковый угол, не нарушая их параллельности, то линия действия их равнодействующей, повернувшись на тот же самый угол, будет вновь проходить через точку С. Точка С носит название центра системы параллельных сил. Таким образом, центром данной системы параллельных сил называется точка, через которую проходит линия действия их равнодействующей при любом повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону. Воспользовавшись формулами аналитической геометрии, можно получить формулы координат
где В случае, если в систему входят силы противоположного направления, причём
1.6.2. По закону всемирного тяготения на все частицы тела, находящегося вблизи земной поверхности, действуют силы притяжения их к Земле, т.е. силы тяжести. Эти силы направлены о радиусу Земли и пересекаются приблизительно в её центре; но так как расстояние до центра Земли чрезвычайно велико по сравнению с расстояниями между частицами тела обычных размеров, то с очень большой точностью можно считать силы тяжести всех отдельных частиц тела параллельными. Равнодействующая сил тяжести всех отдельных частиц тела называется силой тяжести тела. Как бы мы ни поворачивали тело и не изменяли его положение в пространстве, силы тяжести его отдельных частиц останутся параллельными друг другу (вертикальными). Но при таком повороте равнодействующая параллельных сил всегда проходит через одну и ту же точку – центр данной системы параллельных сил. Центр тяжести тела есть такая, неизменно связанная с этим телом, точка, через которую проходит линия действия силы тяжести данного тела при любом положении тела в пространстве. Заметим, что неправильно представлять себе центр тяжести как материальную частицу тела, к которой непосредственно приложена сила тяжести тела. Центр тяжести тела есть всего лишь точка, через которую всегда проходит линия действия силы тяжести тела. Центр тяжести тела может лежать в точке, где вовсе нет материальных частиц, принадлежащих данному телу. Так, например, центром тяжести однородного шара с концентрической полостью служит его геометрический центр.
1.6.3. Так как центр тяжести тела есть центр параллельных сил тяжести его частиц, то его координаты определяются по формулам где Рассмотрим частные случаи. 1) Для однородного (одинаковой плотности по всему объёму) тела координаты центра тяжести определяются по формулем
где 2) Для однородной тонкой пластины постоянной толщины координаты центра тяжести определяются по формулам
где 3) Для однородного тела, площадь поперечного сечения которого одинакова по всей его длине и мала по сравнению с нею, координаты центра тяжести определяются по формулам
где
1.6.4. Теорема. Если однородное тело имеет плоскость (ось, центр) симметрии, то центр тяжести его лежит соответственно в плоскости (на оси, в центре) симметрии. Следствия. 1. Центр тяжести отрезка материальной однородной прямой линии лежит в его середине. 2. Центр тяжести площади однородного параллелограмма лежит в точке пересечения его диагоналей, являющихся центром симметрии параллелограмма. 3. Центры тяжести площадей правильного многоугольника, круга, эллипса и объёма шара лежат в их геометрических центрах.
1.6.5. Аналитический способ. Для определения положения центра тяжести фигур и тел сложной геометрической формы их разбивают на такие части простейшей формы (если, конечно, это возможно), для которых положение центра тяжести известно, а затем определяют положение центра тяжести всей фигуры или тела по соответствующим формулам (см. п. 1.6.3.). Если рассматриваемые фигуры или тела неоднородны, т.е. если они состоят из частей одинаковой плотности, то, разделив их на однородные части, умножают входящие в формулы (1.6.2.) – (1.6.4.) объёмы, площади и длины этих частей на соответствующий каждой части удельный вес. Если в данном теле или фигуре имеются полости или отверстия, то для определения центра тяжести такого тела или фигуры пользуются теми же примами и формулами, считая при этом объёмы и площади вырезанных частей отрицательными. В технической практике широкое распространение имеет стальной прокат различного профиля. Форма этих поперечных сечений, так же как и их размеры, устанавливаются государственными стандартами. В таблицах так зазываемого нормального сортамента прокатной стали, имеющихся в различного рода технических справочниках, приводятся для каждого калибра соответствующего профиля все необходимые сведения, в частности геометрические размеры профиля, площадь сечения, координаты центра тяжести и пр. Пользуясь этими данными, можно указанными выше приемами определить положение центра тяжести и составного сечения, полученного путём соединения нескольких стандартных профилей. Экспериментальный способ осуществляется двумя методами – подвешивания и взвешивания. Метод подвешивания заключается в том, что плоское тело, которое нельзя разбить на простейшие фигуры с известным положением центра тяжести, подвешивают на нити. Прочерчивают линию вдоль этой нити на плоскости тела. Затем эту плоскую фигуру открепляют и подвешивают за другую точку, после чего вновь проводят вертикальную линию (вдоль линии подвеса). Пересечение этих двух линий даёт точку, в которой находится центр тяжести. Метод взвешивания обычно применяется для крупных изделий: самолётов,. Вертолётов и других машин. Если известна масса, например, самолёта, то ставят на весы задние колёса и по показанию весов определяют реакцию
где
Вопросы для самопроверки. 1. Является ли центр тяжести центром параллельных сил? 2. Перечислите способы определения положения центра тяжести твёрдого тела. 3. Расскажите об аналитическом способе определения положения центра тяжести фигуры.
|

 ;
; .
.
 ;
;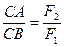 .
.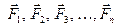 . Если силы данной системы направлены в одну сторону, то её равнодействующая, очевидно, параллельна данным силам и направлена в ту же сторону. Модуль равнодействующей равен сумме модулей составляющих сил:
. Если силы данной системы направлены в одну сторону, то её равнодействующая, очевидно, параллельна данным силам и направлена в ту же сторону. Модуль равнодействующей равен сумме модулей составляющих сил: .
. центра системы параллельных сил:
центра системы параллельных сил:
 - координаты точки приложения силы
- координаты точки приложения силы  .
. , то под
, то под  надо понимать алгебраическое значение силы, т.е. её модуль, взятый со знаком плюс при направлении силы в одну сторону и со знаком минус при направлении силы в другую сторону.
надо понимать алгебраическое значение силы, т.е. её модуль, взятый со знаком плюс при направлении силы в одну сторону и со знаком минус при направлении силы в другую сторону. , (1.6.1.)
, (1.6.1.) - координаты центра тяжести тела,
- координаты центра тяжести тела, 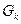 - силя тяжести произвольной частицы тела,
- силя тяжести произвольной частицы тела,  - сила тяжести всего тела.
- сила тяжести всего тела. , (1.6.2.)
, (1.6.2.) -объём одной частицы тела.
-объём одной частицы тела. , (1.6.3.)
, (1.6.3.)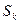 -площадь произвольного элемента фигуры.
-площадь произвольного элемента фигуры. , (1.6.4.)
, (1.6.4.)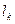 - элемент длины тела.
- элемент длины тела. . Затем составляют одно из уравнений равновесия; удобнее составить сумму моментов относительно точки А (передние колёса):
. Затем составляют одно из уравнений равновесия; удобнее составить сумму моментов относительно точки А (передние колёса): ,
, ,
,  - расстояние между передними колёсами и линией действия силы тяжести.
- расстояние между передними колёсами и линией действия силы тяжести.


