Задачи. 1. Определить характер прямолинейного движения точки по заданному закону движения:
1. Определить характер прямолинейного движения точки по заданному закону движения: а)
2. По данным предыдущего вопроса вычислите все кинематические характеристики движения точки для момента времени t = 2 c, приняв s в метрах.
3. Точка движется по окружности радиуса r = 4 м по закону
4. Точка движется по окружности, радиус которой
5. По окружности радиуса
Тема 1.8. Частные случаи движения точки. 1.8.1. Равномерное движение. 1.8.2. Равнопеременное движение.
1.8.1. Движение точки называется равномерным, если за любые равные промежутки времени точка проходит равные расстояния. Модуль скорости точки при этом движении Если в начальный момент точка находилась не в начале отсчёта расстояний, а на некотором расстоянии
Это уравнение определяет закон равномерного движения точки.
Так как при равномерном движении точки численное значение скорости постоянно, то графиком скорости равномерного движения будет прямая, параллельная оси времени (рис. 1.8.2.).
Если точка совершает криволинейное равномерное движение, то она имеет, как уже было сказано, только нормальное ускорение
1.8.2. Движение точки называется равнопеременным, если за равные, произвольно взятые промежутки времени модуль скорости точки изменяется на одну и ту же величину. Изменение скорости точки по модулю характеризуется, как мы знаем, касательным ускорением. Отсюда следует, что при равнопеременном движении точки значение касательного ускорения
где Закон равнопеременного движения точки имеет вид:
Примером равнопеременного движения точки может служить движение тела по вертикали под действием силы тяжести. Из физики известно, что под действием постоянной силы тело получает постоянное ускорение. Если пренебречь сопротивлением воздуха и изменением силы тяжести в зависимости от высоты тела, то можно считать, что ускорение свободно падающего или брошенного вертикально вверх тела, обычно обозначаемое буквой g, постоянно. Ускорение это изменяется с изменением географической широты и высоты места над уровнем моря, но изменение это незначительно, и потому им обычно пренебрегают, принимая за ускорение свободно падающего тела g=9,81м/с2. Полагая в формулах (1.8.2.) и (1.8.3.) ускорение S = h,получаем формулы для движения тела по вертикали под действием силы тяжести:
В этих формулах перед ускорением g надо брать знак плюс в случае свободного падения тела (равноускоренное движение) и знак минус для движения тела, брошенного вертикально вверх (равнозамедленное движение). В случае, если тело начинает падать без начальной скорости, то
Исключая из этих равенств время t, находим
Отсюда получается хорошо известная формула Галилея
где v — скорость тела при падении его без начальной скорости с высоты Так как формулы (1.8.4.), (1.8.5.) и (1.8.6.) выведены из условия движения тела в пустоте (при отсутствии сопротивления воздуха), то ими можно пользоваться в реальных условиях только в тех случаях, когда сопротивлением воздуха можно пренебречь, т.е. когда вес тела велик по сравнению с силой сопротивления воздуха, а высота
Задачи. 1.
2. Тело, двигаясь равнопеременно из состояния покоя 10 с, достигло скорости 50 м/с. Определить путь, пройденный телом за это время.
3. Торможение поезда, движущегося со скоростью 36 км/ч, начинается за 200 м до остановки. Считая движение поезда равнопеременным, найти время торможения и ускорение, получаемое поездом при торможении.
4. За какое время нужно остановить автомобиль, движущийся со скоростью 90 км/ч, если при быстром торможении ускорение равно – 6 м/с? Каков тормозной путь?
5. На графике изображена зависимость
|

 ; б)
; б)  ; в)
; в)  .
.
 (s – в метрах, t – в секундах). Найти модуль
(s – в метрах, t – в секундах). Найти модуль  ускорения точки и угол
ускорения точки и угол  между вектором ускорения и вектором скорости в тот момент
между вектором ускорения и вектором скорости в тот момент  , когда скорость равна 6 м /с.
, когда скорость равна 6 м /с. =200 м, с касательным ускорением
=200 м, с касательным ускорением 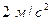 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени, когда её скорость
. Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени, когда её скорость 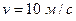 .
. движется точка согласно уравнению
движется точка согласно уравнению 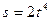 . Определить полное ускорение точки в момент времени
. Определить полное ускорение точки в момент времени  .
. . Отсюда следует, что при прямолинейном равномерном движении точки путь
. Отсюда следует, что при прямолинейном равномерном движении точки путь  .
.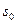 от него, то расстояние точки от начала отсчёта в момент времени t будет равно
от него, то расстояние точки от начала отсчёта в момент времени t будет равно . (1.8.1.)
. (1.8.1.) Так как расстояние точки от начала отсчёта изменяется во времени по линейному закону, то графиком движения точки является прямая линия (рис. 1.8.1.). По графику движения точки можно найти не только расстояние точки от начала отсчёта, но и скорость этого движения (рис. 1.8.1.):
Так как расстояние точки от начала отсчёта изменяется во времени по линейному закону, то графиком движения точки является прямая линия (рис. 1.8.1.). По графику движения точки можно найти не только расстояние точки от начала отсчёта, но и скорость этого движения (рис. 1.8.1.): .
.
 , где
, где  .
. . Поэтому, разделяя переменные в уравнении (1.7.4.) и интегрируя, получим формулу для скорости равнопеременного движения точки
. Поэтому, разделяя переменные в уравнении (1.7.4.) и интегрируя, получим формулу для скорости равнопеременного движения точки , (1.8.2.)
, (1.8.2.)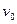 - модуль начальной скорости, т.е. скорости в момент времени t=0. Значение касательного ускорения
- модуль начальной скорости, т.е. скорости в момент времени t=0. Значение касательного ускорения  будем считать положительным при ускоренном движении и отрицательным (касательное ускорение направленно в сторону, противоположную направлению начальной скорости) при замедленном движении. Если
будем считать положительным при ускоренном движении и отрицательным (касательное ускорение направленно в сторону, противоположную направлению начальной скорости) при замедленном движении. Если  , то движение будет равнозамедленным до тех пор, пока скорость
, то движение будет равнозамедленным до тех пор, пока скорость 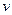 не сделается равной нулю.
не сделается равной нулю. . (1.8.3.)
. (1.8.3.) , (1.8.4.)
, (1.8.4.) . (1.8.5.)
. (1.8.5.) и предыдущие формулы принимают вид
и предыдущие формулы принимают вид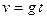 и
и  .
. .
. , (1.8.6.)
, (1.8.6.) .
. Расскажите, как двигалась точка, график скорости которой дан на рисунке.
Расскажите, как двигалась точка, график скорости которой дан на рисунке. для прямолинейного движения. Чему равен путь, пройденный телом?
для прямолинейного движения. Чему равен путь, пройденный телом?



