Тема 1.11. Сложное движение твёрдого тела.
1.11.1.Ппонятие сложного движения тела. 1.11.2. Понятие плоскопараллельного движения тела. 1.11.3.Разложение движения плоской фигуры на поступательное и вращательное. 1.11.4. Скорость точки плоской фигуры. 1.11.5. Мгновенный центр скоростей фигуры. 1.11.6. Сложение вращений вокруг параллельных осей. 1.11.7. Планетарные и дифференциальные передачи
1.11.1.Понятие сложного движения тела аналогично понятию сложного движения точки. В ряде случаев движение тела относительно неподвижной системы отсчета удобно рассматривать как движение сложное, состоящее из двух движений: относительного, т. е. движения тела по отношению к некоторой подвижной системе отсчета, и переносного —движения тела вместе с подвижной системой отсчета по отношению к неподвижной. Всякое сложное движение тела можно свести к той или иной совокупности поступательных и вращательных движений, являющихся не только простейшими, но и основными видами движения твердого тела. Задача определения абсолютного движения тела сводится обычно поэтому к задаче сложения или поступательных движений, или вращательных движений, или вращательного и поступательного движений, в зависимости от того, какими движениями будут переносное и относительное движения тела. Некоторые, особо важные для практики, частные случаи такого сложения движений тела и рассматриваются в данной теме, например способы определения абсолютных скоростей его точек в данный момент времени.
1.11.2. Плоскопараллельным или плоским движением твердого тела называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости. Частным случаем такого движения является уже изученное нами вращение твердого тела вокруг неподвижной оси. При вращательном движении, как мы знаем, все точки тела движутся в плоскостях, перпендикулярных к оси вращения, и, следовательно, любая из этих плоскостей может быть принята за неподвижную, параллельно которой движутся все точки тела. В ряде случаев плоскопараллельное движение тела может быть одновременно и поступательным движением. Однако поступательное движение нельзя, вообще говоря, рассматривать как частный случай плоскопараллельного движения. Не всякое поступательное движение тела есть плоскопараллельное движение, так же как и не всякое плоскопараллельное движение тела есть поступательное движение.
Отсюда следует, что для определения плоскопараллельного движения тела достаточно знать движение неизменяемой плоской фигуры, получающейся при пересечении тела какой-либо плоскостью, параллельной данной неподвижной плоскости. Изучением движения этой плоской фигуры в ее плоскости можно заменить, следовательно, изучение плоскопараллельного движения тела.
Это перемещение плоской фигуры можно представить себе составленным из поступательного и вращательного перемещений (рис. 1.11.4. ). В самом деле, перемещение прямой АВ в положение А'В' можно было бы получить поступательным ее перемещением в положение А'В" или А"В' и вращательным перемещением этой прямой вокруг оси, проходящей соответственно через точку А' или точку В' и перпендикулярной к плоскости фигуры. Произвольная точка, связанная с движущейся фигурой и принимаемая за центр ее поворота, называется полюсом. Нетрудно доказать, что, выбирая различные полюсы, мы изменяем только поступательную часть перемещения фигуры, угол же поворота и направление вращения фигуры от выбора полюса не зависят. Таким образом, мы приходим к выводу: всякое движение плоской фигуры в ее плоскости можно разложить на два движения: 1) поступательное движение вместе с произвольно выбранной точкой фигуры (полюсом) и 2) вращательное движение вокруг этой точки. Так как угол
Определив вращательную скорость Обычно за полюс принимается та точка фигуры, скорость которой в данный момент нам известна.
1.11.5. Можно доказать, что при всяком движении плоской фигуры (кроме поступательного) всегда можно отыскать такую точку, лежащую или на самой движущейся фигуре, или на ее мысленном продолжении, скорость которой в данный момент равна нулю. Неизменно связанная с движущейся плоской фигурой точка Р, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей этой фигуры. Мгновенный центр Р скоростей фигуры всегда лежит на линии, проведенной из какой-либо точки фигуры перпендикулярно к направлению скорости этой точки. Если известны направления скоростей двух каких-либо точек фигуры, то мгновенный центр Р скоростей этой фигуры легко находится как точка пересечения линий, проведенных из данных точек фигуры перпендикулярно к векторам скоростей этих точек (рис. 1.11.6.).
Найдя положение мгновенного центра скоростей Р и зная для данного момента скорость
Направление же вращения фигуры определяется известным направлением скорости ее точки. Указанный выше прием определения мгновенного центра скоростей фигуры как точки пересечения перпендикуляров, восставленных к векторам скоростей двух точек фигуры, неприменим, очевидно, в тех случаях, когда эти скорости параллельны. При этом возможны два случая.
Расстояния данных точек от мгновенного центра скоростей
Так как мгновенный центр скоростей всегда лежит на перпендикуляре, восставленном в любой точке фигуры к направлению ее скорости, а модули скоростей различных точек фигуры в каждый данный момент пропорциональны расстояниям этих точек от мгновенного центра, то положение этой точки Р на перпендикуляре может быть найдено из пропорции Если при этом В практических задачах часто приходится иметь дело со случаями, когда плоская фигура движется так, что ее контур катится без скольжения по некоторой неподвижной кривой. Так как в каждый данный момент у движущейся плоской фигуры может быть только одна точка, имеющая скорость, равную нулю, а при качении без скольжения таковой является точка фигуры, в которой она касается неподвижной кривой, то при качении скольжения контура фигуры по неподвижной кривой мгновенным центром скоростей будет точка касания этого контура с неподвижной кривой.
1.11.6. Абсолютное движение тела., участвующего в двух вращениях вокруг параллельных осей, есть частный случай плоскопараллельного движения тела, и для его определения достаточно рассмотреть движение плоской фигуры S (рис. 1.11.9.), являющейся сечением тела плоскостью, перпендикулярной к данным осям. Движение же плоской фигуры в ее плоскости можно, как известно, рассматривать в каждый данный момент как вращательное движение этой фигуры вокруг соответствующего этому моменту мгновенного центра в некоторой абсолютной угловой скоростью со. При определении положения мгновенного центра скоростей фигуры и ее абсолютной угловой скорости могут быть три случая, каждый из которых мы и рассмотрим. I случай. Оба вращения направлены в одну сторону (рис. 1.11.9.). Обозначим следы осей
· Два вращения, происходящих вокруг параллельных осей в одну сторону, можно в каждый данный момент заменить одним вращением, происходящим в ту же сторону вокруг мгновенной оси, параллельной данным осям, лежащей в одной плоскости с ними и делящей расстояние между ними на части, обратно пропорциональные угловым скоростям составляющих вращений:
· Абсолютная угловая скорость тела равна сумме угловых скоростей составляющих вращений:
II случай. Оба вращения направлены в разные стороны с различной угловой скоростью (рис. 1.11.10.). · Два вращения, происходящие вокруг параллельных осей в разные стороны с различными угловыми скоростями, можно заменить в каждый данный момент одним вращением, происходящим вокруг мгновенной оси, параллельной данным, в сторону вращения с большей угловой скоростью. Мгновенная ось сложного вращения лежит в одной плоскости с данными осями за осью с большей угловой скоростью и отстоит от данных осей на расстояниях, обратно пропорциональных угловым скоростям составляющих вращений:
· Абсолютная угловая скорость тела равна разности угловых скоростей составляющих вращений:
III случай. Оба вращения направлены в разные стороны, а их угловые скорости равны по численному значению (рис. 1.1.11.). · Два вращения тела, происходящие вокруг параллельных осей в разные стороны с равными угловыми скоростями, можно заменить в данный момент одним поступательным его движением, происходящим в направлении, перпендикулярном к плоскости, проведенной через оси составляющих вращений. · Модуль скорости поступательного движения тела равен при этом в данный момент произведению угловой скорости
2.11.7. Колеса, геометрические оси которых неподвижны, называются центральными. Колеса с подвижными геометрическими осями называются сателлитами. Колеса с подвижными осями (2 и 3 на, рис. 1.11.12.) совершают сложное движение, вращаясь одновременно вокруг своих осей ( Планетарные механизмы, в которых одно из центральных колес неподвижно, называются простыми планетарными передачами или, чаще, прост о планетарными передачами. В отличие от простых планетарных передач, планетарные механизмы, в которых нет неподвижных колес, называются дифференциальными передачами или просто дифференциалами. В дифференциальных передачах одно из центральных колес получает вращение вокруг своей неподвижной оси независимо от вращения водила, т. е. получает его от другого источника. Планетарные и дифференциальные механизмы имеют широкое распространение в технике, так как позволяют осуществить большие передаточные отношения при малом числе колес и (в дифференциальных механизмах) сложение двух независимых друг от друга угловых скоростей.
Вопросы для самопроверки. 1. Дайте определение плоскопараллельного движения. 2. Расскажите о подходе к изучению плоскопараллельного движения. 3. Сформулируйте теорему о представлении движения плоской фигуры поступательным перемещением и поворотом. 4. Как выражается скорость произвольной точки плоской фигуры через скорость полюса и скорость вращения вокруг полюса? 5. Дайте определение мгновенного центра скоростей. 6. Расскажите об основных приёмах нахождения мгновенного центра скоростей. 7. Расскажите о сложении вращений вокруг параллельных осей.
|

 Плоскопараллельное движение имеет огромное распространение в технике. Подавляющее большинство встречающихся на практике механизмов являются плоскими, т. е. представляют собой сочленение твердых тел, совершающих плоскопараллельное движение. Таково, например, движение всех звеньев кривошипно-ползунного механизма (рис. 1.11.1), состоящего из кривошипа ОА, ползуна В и шарнирно соединенного с ними шатуна АВ. Все точки каждого из звеньев движутся параллельно некоторой неподвижной плоскости (плоскости чертежа на рис. 1.11.1). Плоскопараллельное движение кривошипа является вместе с тем и вращательным движением вокруг неподвижной оси О. Плоскопараллельное движение ползуна одновременно и поступательное движение вдоль неподвижных направляющих. Плоскопараллельное же движение шатуна не будет ни вращательным (так как шатун не имеет неподвижных точек), ни поступательным (так как прямая АВ не остается при движении шатуна параллельной самой себе).
Плоскопараллельное движение имеет огромное распространение в технике. Подавляющее большинство встречающихся на практике механизмов являются плоскими, т. е. представляют собой сочленение твердых тел, совершающих плоскопараллельное движение. Таково, например, движение всех звеньев кривошипно-ползунного механизма (рис. 1.11.1), состоящего из кривошипа ОА, ползуна В и шарнирно соединенного с ними шатуна АВ. Все точки каждого из звеньев движутся параллельно некоторой неподвижной плоскости (плоскости чертежа на рис. 1.11.1). Плоскопараллельное движение кривошипа является вместе с тем и вращательным движением вокруг неподвижной оси О. Плоскопараллельное движение ползуна одновременно и поступательное движение вдоль неподвижных направляющих. Плоскопараллельное же движение шатуна не будет ни вращательным (так как шатун не имеет неподвижных точек), ни поступательным (так как прямая АВ не остается при движении шатуна параллельной самой себе). Выясним теперь, как можно упростить изучение этого весьма важного вида движения твердого тела. Пусть тело движется параллельно некоторой неподвижной плоскости П (рис. 1.11.2). Если мы пересечем данное тело плоскостью П', параллельной неподвижной плоскости П, то в сечении получится какая-то плоская фигура S. Эта фигура будет перемещаться при движении тела, оставаясь вcё время в той же плоскости П'. Очевидно, что при таком движении тела все его точки, лежащие на перпендикуляре А а к плоскости фигуры S, восставленном в какой-нибудь ее точке а, движутся совершенно одинаково, так же, как и точка а этой фигуры. Все точки тела, лежащие на перпендикуляре Вb, движутся так же, как и точка b фигуры S, и т. д.
Выясним теперь, как можно упростить изучение этого весьма важного вида движения твердого тела. Пусть тело движется параллельно некоторой неподвижной плоскости П (рис. 1.11.2). Если мы пересечем данное тело плоскостью П', параллельной неподвижной плоскости П, то в сечении получится какая-то плоская фигура S. Эта фигура будет перемещаться при движении тела, оставаясь вcё время в той же плоскости П'. Очевидно, что при таком движении тела все его точки, лежащие на перпендикуляре А а к плоскости фигуры S, восставленном в какой-нибудь ее точке а, движутся совершенно одинаково, так же, как и точка а этой фигуры. Все точки тела, лежащие на перпендикуляре Вb, движутся так же, как и точка b фигуры S, и т. д. Заметим также, что положение на плоскости неизменяемой плоской фигуры вполне определяется положением двух любых ее точек или, что все равно, положением какого-либо, прямолинейного отрезка, неизменно связанного с движущейся фигурой. Допустим, что при перемещении этой фигуры неизменно связанный с нею отрезок
Заметим также, что положение на плоскости неизменяемой плоской фигуры вполне определяется положением двух любых ее точек или, что все равно, положением какого-либо, прямолинейного отрезка, неизменно связанного с движущейся фигурой. Допустим, что при перемещении этой фигуры неизменно связанный с нею отрезок  занял в той же плоскости положение
занял в той же плоскости положение  (рис. 1.11.3.). Так как расстояние DEи Слюбой точки Eфигуры от данных ее точек Dи С неизменны, то новое положение этой точки легко определяется построением треугольника
(рис. 1.11.3.). Так как расстояние DEи Слюбой точки Eфигуры от данных ее точек Dи С неизменны, то новое положение этой точки легко определяется построением треугольника 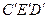 , равного
, равного  .
. 1.11.3. Пусть неизменно связанная с плоской фигурой произвольная прямая перемещается при движении этой фигуры за некоторый промежуток времени из положения АВ в положение А'В' (рис. 1.11.4.).
1.11.3. Пусть неизменно связанная с плоской фигурой произвольная прямая перемещается при движении этой фигуры за некоторый промежуток времени из положения АВ в положение А'В' (рис. 1.11.4.). поворота фигуры и направление ее вращения не зависят от выбора полюса, то и угловая скорость
поворота фигуры и направление ее вращения не зависят от выбора полюса, то и угловая скорость  плоской фигуры от выбора полюса не зависит.
плоской фигуры от выбора полюса не зависит. 1.11.4. Пусть плоская фигура S движется в своей плоскости (рис. 1.11.5.). примем какую-либо произвольную точку А фигуры S за полюс. Тогда можно считать, что по отношению к неподвижной системе отсчёта (связанной с плоскостью, в которой движется фигура) любая другая точка В фигуры участвует одновременно в двух движениях: переносном- вместе с фигурой в её поступательном движении со скоростью
1.11.4. Пусть плоская фигура S движется в своей плоскости (рис. 1.11.5.). примем какую-либо произвольную точку А фигуры S за полюс. Тогда можно считать, что по отношению к неподвижной системе отсчёта (связанной с плоскостью, в которой движется фигура) любая другая точка В фигуры участвует одновременно в двух движениях: переносном- вместе с фигурой в её поступательном движении со скоростью  выбранного полюса и оросительном движении вокруг полюса А. Тогда скорость (абсолютная скорость)
выбранного полюса и оросительном движении вокруг полюса А. Тогда скорость (абсолютная скорость)  любой точки B плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости
любой точки B плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости  первой точки B относительно второй точки A:
первой точки B относительно второй точки A: .
. точки В относительно полюса и зная скорость
точки В относительно полюса и зная скорость  Принимая мгновенный центр Р скоростей фигуры за полюс, легко найти скорости всех остальных точек фигуры в этот момент времени:
Принимая мгновенный центр Р скоростей фигуры за полюс, легко найти скорости всех остальных точек фигуры в этот момент времени:  . Следовательно, скорость любой точки плоской фигуры равна вращательной скорости этой точки вокруг мгновенного центра скоростей фигуры. Тогда
. Следовательно, скорость любой точки плоской фигуры равна вращательной скорости этой точки вокруг мгновенного центра скоростей фигуры. Тогда  , т.е. модули скоростей различных точек фигуры в каждый данный момент пропорциональны расстояниям этих точек от соответствующего данному моменту мгновенного центра скоростей фигуры. Направлены же скорости различных точек фигуры перпендикулярно к отрезкам, соединяющим соответствующие точки с мгновенным центром скоростей, в сторону вращения фигуры (рис. 1.11.6.). Таким образом, скорости различных точек плоской фигуры в каждый данный момент времени распределяются так, как если бы фигура вращалась в этот момент времени вокруг мгновенного центра скоростей, занимающего в разные моменты различные положения как относительно движущейся фигуры, так и относительно неподвижной плоскости, в которой движется фигура.
, т.е. модули скоростей различных точек фигуры в каждый данный момент пропорциональны расстояниям этих точек от соответствующего данному моменту мгновенного центра скоростей фигуры. Направлены же скорости различных точек фигуры перпендикулярно к отрезкам, соединяющим соответствующие точки с мгновенным центром скоростей, в сторону вращения фигуры (рис. 1.11.6.). Таким образом, скорости различных точек плоской фигуры в каждый данный момент времени распределяются так, как если бы фигура вращалась в этот момент времени вокруг мгновенного центра скоростей, занимающего в разные моменты различные положения как относительно движущейся фигуры, так и относительно неподвижной плоскости, в которой движется фигура.
 1. Скорости двух точек А и В фигуры параллельны, но эти точки не лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.7.).
1. Скорости двух точек А и В фигуры параллельны, но эти точки не лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.7.). . Угловая скорость фигуры в данный момент
. Угловая скорость фигуры в данный момент  , и вращение фигуры в этот момент, следовательно, отсутствует. А так как всякое абсолютное плоское движение фигуры можно рассматривать как совокупность поступательного движения со скоростью произвольно выбранного полюса и вращательного движения вокруг этого полюса (с угловой скоростью
, и вращение фигуры в этот момент, следовательно, отсутствует. А так как всякое абсолютное плоское движение фигуры можно рассматривать как совокупность поступательного движения со скоростью произвольно выбранного полюса и вращательного движения вокруг этого полюса (с угловой скоростью  , независящий от выбора полюса), то абсолютные скорости точек фигуры в данном случае равны только скорости полюса. Другими словами, в этом случае фигура совершает в данный момент поступательное движение, и скорости всех её точек в этот момент равны между собой.
, независящий от выбора полюса), то абсолютные скорости точек фигуры в данном случае равны только скорости полюса. Другими словами, в этом случае фигура совершает в данный момент поступательное движение, и скорости всех её точек в этот момент равны между собой. 2. Скорости двух точек А и В фигуры параллельны, и эти точки лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.8.).
2. Скорости двух точек А и В фигуры параллельны, и эти точки лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.8.). (рис. 1.11.8.).
(рис. 1.11.8.). то фигура совершает в данный момент поступательное движение (так же как и в предыдущем случае).
то фигура совершает в данный момент поступательное движение (так же как и в предыдущем случае). и
и  в плоскости фигуры S точками
в плоскости фигуры S точками  и
и 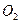 .
.
 .
. .
. .
. между осями составляющих вращений:
между осями составляющих вращений: .
. Планетарными и дифференциальными передачами называются механизмы, в которых имеются колеса с подвижными осями, вращающимися вместе с так называемым водилом (Н на рис. 1.11.12.) вокруг неподвижной оси.
Планетарными и дифференциальными передачами называются механизмы, в которых имеются колеса с подвижными осями, вращающимися вместе с так называемым водилом (Н на рис. 1.11.12.) вокруг неподвижной оси.


