1. К двум материальным точкам массы 2 и 8 кг приложены одинаковые силы. Сравните между собой значения ускорений этих точек.
2.  Определите числовое значение и направление ускорения точки А массой 2 кг под действием приложенной к ней системы сил, если
Определите числовое значение и направление ускорения точки А массой 2 кг под действием приложенной к ней системы сил, если  ,
, 
 ,
,  ,
,  .
.
Тема 1.13. Основы кинетостатики.
1.13.1. Принцип  Аламбера.
Аламбера.
1.13.2. Понятие силы инерции.
1.13.1. Принцип, который обычно связывают с именем выдающегося французского ученого Ж.  Аламбера (1717—1783), лежит в основе важного метода динамики, позволяющего задачи динамики формально сводить к задачам статики.
Аламбера (1717—1783), лежит в основе важного метода динамики, позволяющего задачи динамики формально сводить к задачам статики.
 Допустим, что к несвободной материальной точке М массы т приложена некоторая активная сила
Допустим, что к несвободной материальной точке М массы т приложена некоторая активная сила  . Освобождая мысленно точку от связей, заменим их действие на точку силой
. Освобождая мысленно точку от связей, заменим их действие на точку силой  реакции этих связей. Тогда точку М можно считать свободной, но находящейся под действием силы
реакции этих связей. Тогда точку М можно считать свободной, но находящейся под действием силы  , являющейся равнодействующей сил
, являющейся равнодействующей сил  и
и  (рис. 1.13.1.). По основному уравнению динамики точки
(рис. 1.13.1.). По основному уравнению динамики точки  . Условно приложим к точке М еще и вектор
. Условно приложим к точке М еще и вектор  .
.
Вектор 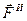 , равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки, называется силой инерции этой точки. Геометрическая сумма сил
, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки, называется силой инерции этой точки. Геометрическая сумма сил
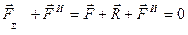
и совокупность сил  представляет, следовательно, уравновешенную систему.
представляет, следовательно, уравновешенную систему.
Симла 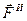 инерции материальной точки условно прилагается к самой материальной точке, и потому получающееся при этом равновесие является не действительным, а лишь условным, воображаемым равновесием.
инерции материальной точки условно прилагается к самой материальной точке, и потому получающееся при этом равновесие является не действительным, а лишь условным, воображаемым равновесием.
Однако такое условное присоединение силы инерции точки к числу сил, в действительности к ней приложенных, позволяет применить к решению задач динамики хорошо известные приемы статики и лежит в основе метода, называемого методом кинетостатики.
Идея метода кинетостатики может быть сформулирована для материальной точки следующим образом: во всякий момент движения материальной точки приложенные к ней активные силы, силы реакций наложенных на нее связей и сила инерции данной точки (условно приложенная к ней самой) взаимно уравновешиваются.
Метод кинетостатики вследствие своей простоты и наглядности широко применяется в технической практике для решения задач динамики. Особенно удобен этот метод для определения так называемых динамических реакций связей, т. е. реакций, возникающих в связях при движении системы. Этим методом можно пользоваться и для определения ускорений тел, входящих в состав системы.
Наряду с этим заметим, что все без исключения задачи динамики можно решать и без применения метода кинетостатики, не пользуясь вовсе понятием сил инерции.
1.13.2. В природе не бывает одностороннего действия сил. Если материальная точка массы т в результате взаимодействия с другими, окружающими ее телами, приобрела некоторое ускорение  , то к этим телам, согласно третьему основному закону механики, приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна
, то к этим телам, согласно третьему основному закону механики, приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна  , т.е. равна силе инерции точки. Только формально, так как сложение сил приложенных к различным телам физического смысла не имеет.
, т.е. равна силе инерции точки. Только формально, так как сложение сил приложенных к различным телам физического смысла не имеет.
Реально существуют лишь составляющие этой силы, приложенные к тем телам, которые являются источником активных сил, действующих на движущуюся с ускорением материальную точку, и к связям, наложенным на точку. О силе инерции  можно говорить как о реальной силе лишь в том случае, когда на точку действует только одно тело.
можно говорить как о реальной силе лишь в том случае, когда на точку действует только одно тело.
Рассмотрим такой пример. Рабочий катит перед собой по рельсам вагонетку, сообщая ей ускорение  . Для простоты считаем, что вагонетка движется по горизонтальному прямолинейному пути и никаких сопротивлений своему движению не встречает. Следовательно, источником силы, сообщающей вагонетке ускорение
. Для простоты считаем, что вагонетка движется по горизонтальному прямолинейному пути и никаких сопротивлений своему движению не встречает. Следовательно, источником силы, сообщающей вагонетке ускорение  , является только рабочий. По основному закону динамики для сообщения вагонетке этого ускорения рабочий должен приложить к ней силу
, является только рабочий. По основному закону динамики для сообщения вагонетке этого ускорения рабочий должен приложить к ней силу  , где т —масса вагонетки. Всякое действие одного тела на другое всегда сопровождается равным и противоположно направленным действием второго тела на первое. Следовательно, рабочий будет встречать со стороны вагонетки силу противодействия
, где т —масса вагонетки. Всякое действие одного тела на другое всегда сопровождается равным и противоположно направленным действием второго тела на первое. Следовательно, рабочий будет встречать со стороны вагонетки силу противодействия  , равную по модулю силе
, равную по модулю силе  давления рабочего на вагонетку и направленную в противоположную сторону, т. е. в сторону, противоположную ускорению. Очевидно, что сила
давления рабочего на вагонетку и направленную в противоположную сторону, т. е. в сторону, противоположную ускорению. Очевидно, что сила 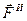 вагонетки приложена не к ней самой, а к руке рабочего (рис. 1.13.2.).
вагонетки приложена не к ней самой, а к руке рабочего (рис. 1.13.2.).
 Необходимо всегда иметь в виду, что, применяя метод кинетостатики, мы лишь условно прилагаем силу инерции материальной точки к самой точке.
Необходимо всегда иметь в виду, что, применяя метод кинетостатики, мы лишь условно прилагаем силу инерции материальной точки к самой точке.
 В общем случае движения точки по, криволинейной траектории ускорение
В общем случае движения точки по, криволинейной траектории ускорение  точки, как мы знаем, удобно разлагать на две составляющие: касательное (тангенсальное) ускорение
точки, как мы знаем, удобно разлагать на две составляющие: касательное (тангенсальное) ускорение 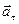 (
( )направленное по касательной к траектории движения, и нормальное ускорение
)направленное по касательной к траектории движения, и нормальное ускорение  (
(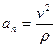 ,
,  - радиус кривизны траектории в данном положении материальной точки), направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке М массы т, движущейся со скоростью
- радиус кривизны траектории в данном положении материальной точки), направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке М массы т, движущейся со скоростью  , приложена сила
, приложена сила  , направление которой образует с направлением скорости
, направление которой образует с направлением скорости  некоторый угол (рис. 1.13.3.). Точка в этом случае будет двигаться по криволинейному пути с ускорением
некоторый угол (рис. 1.13.3.). Точка в этом случае будет двигаться по криволинейному пути с ускорением  , направленным одинаково с силой
, направленным одинаково с силой  .
.
Очевидно, что при криволинейном движении точки приложенную к ней силу  можно разложить на две составляющие: касательную силу
можно разложить на две составляющие: касательную силу  , изменяющую модуль скорости точки, и нормальную силу
, изменяющую модуль скорости точки, и нормальную силу  , изменяющую направление скорости точки.
, изменяющую направление скорости точки.
При криволинейном движении точки её силу инерции также можно разложить на две составляющие: касательную силу инерции  , напрвленную противоположно касательному ускорению точки, и нормальную силу инерции
, напрвленную противоположно касательному ускорению точки, и нормальную силу инерции  , направленную противоположно нормальному ускорению точки.
, направленную противоположно нормальному ускорению точки.
При несвободном криволинейном движении точки, действующей на неё нормальной силой будет реакция связи, заставляющая точку отклоняться от прямолинейного пути и, следовательно, сообщающая ей соответствующее нормальное ускорение. Силой же, действующей на связь, будет нормальная сила инерции данной точки.
 Положим, что в криволинейном желобе лежит шар (рис. 1.13.4.). Если сообщить ему толчок в направлении оси желоба, то возникнут одновременно две силы: нормальная реакция стенок желоба на шар
Положим, что в криволинейном желобе лежит шар (рис. 1.13.4.). Если сообщить ему толчок в направлении оси желоба, то возникнут одновременно две силы: нормальная реакция стенок желоба на шар  и нормальная сила инерции
и нормальная сила инерции  —давление шара на стенки жалоба, направленная по той же нормали от центра. Если желоб взять резиновым, то действие нормальной силы инерции наглядно проявится выпучиванием при движении шара наружной поверхности желоба.
—давление шара на стенки жалоба, направленная по той же нормали от центра. Если желоб взять резиновым, то действие нормальной силы инерции наглядно проявится выпучиванием при движении шара наружной поверхности желоба.
 Подвешенное к нити тело (рис. 1.13.5.) натягивает ее при покое с силой, равной по модулю силе тяже- сти
Подвешенное к нити тело (рис. 1.13.5.) натягивает ее при покое с силой, равной по модулю силе тяже- сти  тела. Будучи же приведено в колебание, тело натягивает нить в момент ее перехода через вертикальное положение с силой
тела. Будучи же приведено в колебание, тело натягивает нить в момент ее перехода через вертикальное положение с силой  (
( ). При быстром вращении центробежная сила инерции тела, приложенная к нити, осуществляющей связь, заставляющую тело совершать криволинейное движение, может настолько увеличить натяжение нити, что произойдет ее разрыв. В момент разрыва нити исчезнет реакция связи (сила
). При быстром вращении центробежная сила инерции тела, приложенная к нити, осуществляющей связь, заставляющую тело совершать криволинейное движение, может настолько увеличить натяжение нити, что произойдет ее разрыв. В момент разрыва нити исчезнет реакция связи (сила  ), приложенная к телу, так как исчезает связь, делавшая его движение несвободным; в тот же самый момент исчезнет и нормальная сила инерции, и тело будет перемещаться по касательной к окружности в той ее точке, в которой оно находилось в момент разрыва нити.
), приложенная к телу, так как исчезает связь, делавшая его движение несвободным; в тот же самый момент исчезнет и нормальная сила инерции, и тело будет перемещаться по касательной к окружности в той ее точке, в которой оно находилось в момент разрыва нити.
Аналогичным действием нормальной силы инерции объясняется и происходящий иногда разрыв маховиков при их очень быстром вращении. Если вся масса вращающегося тела распределена симметрично относительно его оси вращения, то нормальные силы инерции, развиваемые отдельными его частями, сказываются только в возникновении динамических напряжений (внутренних усилий) в материале тела. Эти динамические напряжения при больших скоростях могут достигать весьма больших значений, и с ними безусловно нужно считаться. Но если масса вращающегося тела распределена несимметрично относительно оси вращения, то нормальные силы инерции отдельных частиц тела оказывают также еще и добавочное давление на подшипники, увеличивая трение в подшипниках и их износ. Вследствие вращения тела равнодействующая неуравновешенных сил инерции все время изменяет свое направление, а это ведет к нежелательной вибрации тела. Вопрос об уравновешивании сил инерции имеет большое значение в современном машиностроении и рассматривается в теории механизмов и машин. При проектировании каждой новой машины необходимо учитывать силы инерции, которые могут возникнуть в ней при различных условиях работы.
Вопросы для самопроверки.
1. Что называется силой инерции точки?
2. Сформулируйте принцип  Аламбера.
Аламбера.

 Определите числовое значение и направление ускорения точки А массой 2 кг под действием приложенной к ней системы сил, если
Определите числовое значение и направление ускорения точки А массой 2 кг под действием приложенной к ней системы сил, если  ,
, 
 ,
,  ,
,  .
.
 Аламбера.
Аламбера. Допустим, что к несвободной материальной точке М массы т приложена некоторая активная сила
Допустим, что к несвободной материальной точке М массы т приложена некоторая активная сила  . Освобождая мысленно точку от связей, заменим их действие на точку силой
. Освобождая мысленно точку от связей, заменим их действие на точку силой  реакции этих связей. Тогда точку М можно считать свободной, но находящейся под действием силы
реакции этих связей. Тогда точку М можно считать свободной, но находящейся под действием силы  , являющейся равнодействующей сил
, являющейся равнодействующей сил  . Условно приложим к точке М еще и вектор
. Условно приложим к точке М еще и вектор  .
.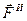 , равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки, называется силой инерции этой точки. Геометрическая сумма сил
, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки, называется силой инерции этой точки. Геометрическая сумма сил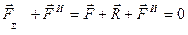
 представляет, следовательно, уравновешенную систему.
представляет, следовательно, уравновешенную систему. , то к этим телам, согласно третьему основному закону механики, приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна
, то к этим телам, согласно третьему основному закону механики, приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна  , т.е. равна силе инерции точки. Только формально, так как сложение сил приложенных к различным телам физического смысла не имеет.
, т.е. равна силе инерции точки. Только формально, так как сложение сил приложенных к различным телам физического смысла не имеет. Необходимо всегда иметь в виду, что, применяя метод кинетостатики, мы лишь условно прилагаем силу инерции материальной точки к самой точке.
Необходимо всегда иметь в виду, что, применяя метод кинетостатики, мы лишь условно прилагаем силу инерции материальной точки к самой точке. В общем случае движения точки по, криволинейной траектории ускорение
В общем случае движения точки по, криволинейной траектории ускорение 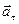 (
( )направленное по касательной к траектории движения, и нормальное ускорение
)направленное по касательной к траектории движения, и нормальное ускорение  (
(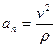 ,
,  - радиус кривизны траектории в данном положении материальной точки), направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке М массы т, движущейся со скоростью
- радиус кривизны траектории в данном положении материальной точки), направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке М массы т, движущейся со скоростью  , приложена сила
, приложена сила  , направленным одинаково с силой
, направленным одинаково с силой  , изменяющую модуль скорости точки, и нормальную силу
, изменяющую модуль скорости точки, и нормальную силу  , изменяющую направление скорости точки.
, изменяющую направление скорости точки. , напрвленную противоположно касательному ускорению точки, и нормальную силу инерции
, напрвленную противоположно касательному ускорению точки, и нормальную силу инерции  , направленную противоположно нормальному ускорению точки.
, направленную противоположно нормальному ускорению точки. Положим, что в криволинейном желобе лежит шар (рис. 1.13.4.). Если сообщить ему толчок в направлении оси желоба, то возникнут одновременно две силы: нормальная реакция стенок желоба на шар
Положим, что в криволинейном желобе лежит шар (рис. 1.13.4.). Если сообщить ему толчок в направлении оси желоба, то возникнут одновременно две силы: нормальная реакция стенок желоба на шар  и нормальная сила инерции
и нормальная сила инерции  Подвешенное к нити тело (рис. 1.13.5.) натягивает ее при покое с силой, равной по модулю силе тяже- сти
Подвешенное к нити тело (рис. 1.13.5.) натягивает ее при покое с силой, равной по модулю силе тяже- сти  тела. Будучи же приведено в колебание, тело натягивает нить в момент ее перехода через вертикальное положение с силой
тела. Будучи же приведено в колебание, тело натягивает нить в момент ее перехода через вертикальное положение с силой  (
( ). При быстром вращении центробежная сила инерции тела, приложенная к нити, осуществляющей связь, заставляющую тело совершать криволинейное движение, может настолько увеличить натяжение нити, что произойдет ее разрыв. В момент разрыва нити исчезнет реакция связи (сила
). При быстром вращении центробежная сила инерции тела, приложенная к нити, осуществляющей связь, заставляющую тело совершать криволинейное движение, может настолько увеличить натяжение нити, что произойдет ее разрыв. В момент разрыва нити исчезнет реакция связи (сила 


