Тангенсальная составляющая ускорения
т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю. Найдём вторую составляющую ускорения. Можно доказать, что при
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру её кривизны (поэтому её называют также центростремительным ускорением).
В зависимости от тангенсальной и нормальной составляющих ускорения движение можно классифицировать следующим образом: 1) 2) 3) 4) 5) 6) 7)
Вопросы для самопроверки. 1. Что называется материальной точкой? Почему в механике вводят такую модель? 2. Что такое система отсчёта? 3. Что такое вектор перемещения? Всегда ли модуль вектора перемещения равен отрезку пути, пройденному точкой? 4. Дать определение векторов средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения. 5. Что характеризует тангенсальная составляющая ускорения? Нормальная составляющая ускорения? Каковы их модули? 6. Возможны ли движения, при которых отсутствует нормальное ускорение? Тангенсальное ускорение? Приведите примеры.
|

 (1.7.5.)
(1.7.5.) векторы
векторы  и
и  оказываются взаимно перпендикулярными. Так как вектор скорости
оказываются взаимно перпендикулярными. Так как вектор скорости  , (1.7.6.)
, (1.7.6.) Полное ускорение тела есть геометрическая сумма тангенсальной и нормальной составляющих (рис. 1.7.6.):
Полное ускорение тела есть геометрическая сумма тангенсальной и нормальной составляющих (рис. 1.7.6.): . (1.7.7.)
. (1.7.7.) ,
,  - прямолинейное равномерное движение;
- прямолинейное равномерное движение; ,
,  ,
,  - равномерное движение по окружности;
- равномерное движение по окружности;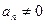 - равномерное криволинейное движение;
- равномерное криволинейное движение;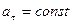 ,
, 


