Тема 1.16. Общие теоремы динамики.
1.16.1. Количество движения и импульс силы. 1.16.2. Теорема об изменении количества движения точки. 1.16.3. Потенциальная и кинетическая энергии. 1.16.4. Теорема об изменении кинетической энергии точки. 1.16.5. Основное уравнение динамики для вращательного движения твёрдого тела.
1.16.1. Количеством движения материальной точки называется вектор Так как масса точки есть скалярная положительная величина, то направление вектора количества движения точки всегда совпадает с направлением ее скорости, модуль же количества движения равняется произведению массы точки на модуль скорости точки. Из совпадения направлений векторов ее скорости: В Международной системе единиц (СИ) количество движения измеряется в килограмм-метрах в секунду, т. е. в кг-м/с. С понятием количества движения тесно связано понятие импульса силы. Рассмотрим только случай, когда на точку действует постоянная по модулю и по направлению сила. Импульсом . Так как время есть скалярная величина, то направление вектора совпадает с направлением вектора
Так же, как и количество движения, в СИ импульс выражается в кг-м/с.
1.16.2. Зависимость между вектором ускорения
Спроецировав это векторное равенство на координатную ось х, получим
Но, как известно из кинематики, проекция ускорения на неподвижную координатную ось равна первой производной по времени от проекции скорости точки на ту же ось:
Подставляя это значение в предыдущее уравнение, получим
или, вводя в левой части равенства постоянный множитель т под знак производной,
Производная по времени от проекции на какую-либо ось количества движения точки равна проекции на ту же ось силы, действующей на точку. Умножая обе части равенства (1.16.1.) на
Интегрируя обе части равенства в соответствующих пределах и обозначая проекцию начальной (в момент t = 0) скорости точки на ось х через
или
Совершенно так же получаются и аналогичные уравнения в проекциях на оси у и z:
Уравнения (1.16.2.) и (1.16.3.) выражают собой теорему об изменении количества движения материальной точки (в проекциях на оси координат), которую можно сформулировать следующим образом: изменение проекции количества движения точки на какую-либо ось равно проекции на ту же ось импульса силы, действующей на точку, за то же время. Теорема об изменении количества движения, точки, как и другие так называемые основные теоремы' динамики, является следствием второго основного закона динамики и вытекающего из него основного уравнения динамики и представляет собой результат математического преобразования этого уравнения. Теоремой об изменении количества движения точки следует пользоваться для решения тех задач, в которых устанавливается зависимость между массой материальной точки, ее скоростью в начальный и конечный моменты движения, силой и временем ее действия, причем одна из этих величин является искомой, а остальные—известными величинами. Если на точку действует одновременно не одна, а несколько сил, то под проекциями Всякую несвободную материальную точку, т. е. точку, движение которой ограничено некоторыми условиями (связями), можно мысленно освободить от связей, заменив их действие на точку реакциями этих связей. Следовательно, рассматривая движение несвободной точки, надо в число сил, на нее действующих, включить и реакции всех наложенных на точку связей.
1.16.3. Одним из основных физических понятий является энергия. В механике под энергией тела понимается величина, характеризующая его способность совершать в определенных условиях ту или иную работу. При этом различают два вида так называемой механической энергии: потенциальную и кинетическую. Потенциальной энергией Потенциальная энергия тела измеряется той работой, которую оно может совершить при перемещении его из данного положения в какое-либо другое. Так, например, тело, сила тяжести которого равна Нужно иметь в виду, что понятие потенциальной энергии— понятие относительное и имеет смысл только при указании двух сопоставляемых друг с другом положений тела. Очевидно, например, что потенциальная энергия тела, лежащего на Земле у края колодца, относительно данного места земной поверхности будет равна нулю. В то же время это тело обладает определенной потенциальной энергией относительно дна колодца, и притом тем большей, чем глубина последнего. Потенциальной энергией обладает и всякое тело, находящееся в состоянии упругой деформации, например: растянутая, сжатая или закрученная пружина, сжатый воздух или газ и т. д. Возникающие при деформации тела, т. е. при изменении во взаимном расположении его частиц, силы упругости совершат определенную работу в процессе восстановления формы тела, когда будут устранены причины, удерживающие тело в данном деформированном состоянии. Кинетической энергией тела называется энергия его механического движения. Кинетическая энергия измеряется той работой, которую движущееся тело может совершить при его затормаживании до остановки. Кинетическая энергия материальной точки зависит только от массы точки и ее скорости в момент начала торможения. Чем больше масса точки и чем больше ее скорость, тем большей кинетической энергией обладает точка. Так, летящий с большой скоростью снаряд, встретив на своем пути препятствия в виде толстых стен, брони и т. п. и теряя при этом свою скорость, преодолевает сопротивление этих препятствий, т. е. совершает огромную работу. Как это будет видно из следующего пункта, за меру кинетической энергии
Энергия, как и работа, выражается в джоулях (килоджоулях, мегаджоулях).
Согласно тому же закону векторы силы
Но так как
Интегрируя левую часть последнего равенства в пределах изменения скорости от
или
где А- работа силы Равенство (1.16.4.) может быть сформулировано следующим образом: изменение кинетической энергии материальной точки на некотором пути равно работе приложенной к ней силы на том же пути (теорема об изменении кинетической энергии материальной точки). Если движение материальной точки совершалось под действием не одной, а нескольких приложенных к ней сил, то под работой А в уравнении (1.16.4.) надо понимать работу равнодействующей этих сил, равную, как было доказано ранее, алгебраической сумме работ всех составляющих сил. Если под действием сил сопротивления, приложенных к данной материальной точке, точка останавливается, то конечная скорость
Работа сил сопротивления, как мы знаем, всегда отрицательна, потому отрицательной будет и правая часть написанного выше равенства. Таким образом, выражение Теорема об изменениии кинетической энергии точки позволяет определить работу приложенных к ней сил при переходе точки из одного положения в другое и в тех случаях (переменной силы и криволинейного движения точки), когда непосредственное вычисление работы по формуле (1.15.3.) затруднительно. Для этого надо только знать массу точки и модули ее скорости в начальном и конечном положениях. Если же, наоборот, мы имеем возможность непосредственного определения работы приложенных к точке сил, то, зная массу точки и модуль ее скорости в одном положении, легко найти, пользуясь данной теоремой, модуль скорости точки в другом положении. Теорема об изменении кинетической энергии точки дает наиболее простой способ решения тех задач, в которых устанавливается зависимость между действующей на точку силой, скоростью точки и пройденным ею путем.
1.16.5. Пусть твердое тело, имеющее возможность вращаться вокруг неподвижной оси z, находится под действием приложенной к нему системы сил Если же эта сумма моментов не равна нулю, то тело вращается вокруг оси z с некоторым угловым ускорением Чтобы определить угловое ускорение тела, воспользуемся методом кинетостатики. Условно присоединив к приложенным к телу активным силам силы инерции всех его частиц, мы можем применить к полученной системе сил соответствующее условие равновесия. В рассматриваемом случае это условие принимает следующий вид: сумма моментов приложенных к телу активных сил и сил инерции всех его частиц относительно оси вращения тела должна равняться нулю.
Все центробежные силы инерции пересекают ось zвращения тела, и, следовательно, моменты их относительно этой оси равны нулю. Касательная сила инерции частицы тк дает относительно оси вращения тела момент Составляя сумму моментов касательных сил инерции для всех элементарных частиц тела, будем иметь Обозначим Моментом инерции Следовательно, сумма моментов сил инерции всех материальных частиц тела, вращающегося вокруг неподвижной оси, равна
Прибавляя эту сумму к сумме моментов всех приложенных к телу активных сил, мы получим, в соответствии с установленным выше условием, следующее равенство:
Для краткости будем называть алгебраическую сумму моментов всех приложенных к телу активных сил относительно оси z вращения тела вращающим моментом и обозначать его
Таким образом, приходим к следующему равенству:
Вращающий момент Так как момент инерции J данного тела относительно данной оси есть величина постоянная, то, как это следует из уравнения (1.16.5.), при постоянном вращающем моменте Так, если момент приложенных к валу машины движущих сил равен по модулю моменту сил сопротивления, то вал будет вращаться равномерно. Если момент движущих сил больше момента сил сопротивления, то вал вращается ускоренно. Если момент движущих сил будет меньше момента сил сопротивления, то вал будет вращаться замедленно. Нетрудно заметить, что по своему виду основное уравнение (1.16.5.) динамики для вращательного движения тела напоминает основное уравнение динамики для материальной точки (или, что то же, для поступательного движения тела):
Из сопоставления этих уравнений видно, что момент инерции тела играет при его вращательном движении ту же роль, что масса тела при поступательном движении. Так же как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении вокруг этой оси. При одном и том же вращающем моменте угловое ускорение тела будет тем меньше, чем больше момент инерции тела относительно оси вращения. Существенное отличие момента инерции тела от его массы заключается, однако, в том, что масса тела является для него величиной постоянной, тогда как момент инерции тела зависит не только от самой вращающейся массы, но и от распределения этой массы относительно оси вражения. Например, одну и ту же длинную палку значительно легче привести руками в быстрое вращение вокруг её продольной оси, чем вокруг оси, перпендикулярной к её длине. Объясняется это тем, что момент инерции палки в первом случае значительно меньше, чем во втором. Поэтому для сообщения одинакового углового ускорения в первом случае потребуется значительно меньший вращающий момент. Колесо с тяжёлым ободом и лёгкой втулкой обладает большим моментом инерции, чем колесо той же массы, но с тяжёлой втулкой и лёгким ободом, так как в первом случае большая часть массы находится на наибольшем расстоянии от оси вращения. А так как чем значительнее момент инерции тела, тем труднее его движение, то этим и пользуются в маховиках, служащих для выравнивания хода машины, делая их значительного диаметра и распределяя большую часть их массы по ободу.
Вопросы для самопроверки. 1. Дайте определение количества движения точки. 2. Что называется импульсом силы за конечный промежуток времени? 3. Сформулируйте теорему об изменении количества движения точки. 4. Что называется кинетической энергией точки? 5. Сформулируйте теорему об изменении кинетической энергии точки. 6. Что называется мометом инерции тела относительно оси? 7. Вывести основное уравнение динамики для вращательного движения тела.
|

 , равный произведению массы
, равный произведению массы  точки на вектор
точки на вектор  ее скорости.
ее скорости. ,
,  и
и  .
. постоянной по модулю и по направлению силы за некоторый промежуток времени называется вектор, равный произведению вектора
постоянной по модулю и по направлению силы за некоторый промежуток времени называется вектор, равный произведению вектора 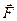 силы на данный промежуток времени:
силы на данный промежуток времени: ,
, 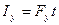 и
и 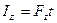 .
. точки и вектором приложенной к нему силы
точки и вектором приложенной к нему силы  .
. .
. .
. .
. . (1.16.1.)
. (1.16.1.) , будем иметь
, будем иметь .
. и проекцию конечной (в момент времени t =
и проекцию конечной (в момент времени t =  ) скорости точки на ту же ось через
) скорости точки на ту же ось через  получим
получим ,
,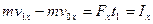 . (1.16.2.)
. (1.16.2.) и
и  . (1.16.3.)
. (1.16.3.) силы, действующей на точку, надо понимать, согласно закону независимости действия сил, проекцию равнодействующей всех сил, приложенных к точке, равную, как известно, алгебраической сумме проекций составляющих сил на соответствующую ось.
силы, действующей на точку, надо понимать, согласно закону независимости действия сил, проекцию равнодействующей всех сил, приложенных к точке, равную, как известно, алгебраической сумме проекций составляющих сил на соответствующую ось. , или энергией положения, называетсл энергия, зависящая только от взаимного расположения тел или частей одного и того же тела.
, или энергией положения, называетсл энергия, зависящая только от взаимного расположения тел или частей одного и того же тела.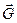 , удерживаемое на высоте h над Землей, обладает относительно этой поверхности потенциальной энергией, равной произведению
, удерживаемое на высоте h над Землей, обладает относительно этой поверхности потенциальной энергией, равной произведению 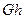 , т. е. той работе, которую оно может совершить при падении на Землю (если будут устранены препятствия такому движению тела).
, т. е. той работе, которую оно может совершить при падении на Землю (если будут устранены препятствия такому движению тела). материальной точки следует принять половину произведения массы
материальной точки следует принять половину произведения массы  ее скорости:
ее скорости: .
. 1.16.4. Пусть материальная точка М массы т под действием приложенной к ней силы
1.16.4. Пусть материальная точка М массы т под действием приложенной к ней силы  и спроецировав обе части последнего равенства на направление скорости, будем иметь
и спроецировав обе части последнего равенства на направление скорости, будем иметь .
. , то получим
, то получим  . Умножим обе части последнего равенства на малое перемещение
. Умножим обе части последнего равенства на малое перемещение  :
: 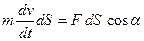 или
или  ,
,  .
. до
до  а правую—соответственно в пределах от 0 до S, будем иметь
а правую—соответственно в пределах от 0 до S, будем иметь ,
, , (1.16.4.)
, (1.16.4.) .
. представляет собой работу, которую может совершить данная точка, движущаяся со скоростью
представляет собой работу, которую может совершить данная точка, движущаяся со скоростью  (рис. 1.16.2.). Условием равновесия тела, имеющего неподвижную ось, является, как известно из статики, равенство нулю алгебраической суммы моментов всех приложенных к телу активных сил
(рис. 1.16.2.). Условием равновесия тела, имеющего неподвижную ось, является, как известно из статики, равенство нулю алгебраической суммы моментов всех приложенных к телу активных сил  , знак которого, очевидно, совпадает со знаком главного момента приложенных к телу сил.
, знак которого, очевидно, совпадает со знаком главного момента приложенных к телу сил. Разобьем данное тело на элементарные материальные частицы. Обозначим массу одной из таких частиц
Разобьем данное тело на элементарные материальные частицы. Обозначим массу одной из таких частиц  (рис. 1.16.2.), а ее расстояние до оси -
(рис. 1.16.2.), а ее расстояние до оси -  . Силу инерции каждой такой частицы разложим на составляющие: центробежную, равную по модулю
. Силу инерции каждой такой частицы разложим на составляющие: центробежную, равную по модулю 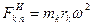 и направленную по радиусу от центра, и касательную, равную по модулю
и направленную по радиусу от центра, и касательную, равную по модулю 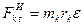 , и направленную по перпендикуляру к радиусу в сторону, противоположную касательному ускорению. Направления сил
, и направленную по перпендикуляру к радиусу в сторону, противоположную касательному ускорению. Направления сил  и
и  показаны на рис. 1.16.2.; при этом мы считаем, что главный момент приложенных к телу сил
показаны на рис. 1.16.2.; при этом мы считаем, что главный момент приложенных к телу сил  . При отрицательном угловом ускорении направление касательной силы инерции изменится на противоположное.
. При отрицательном угловом ускорении направление касательной силы инерции изменится на противоположное. .
. .
. через
через  и назовем моментом инерции тела относительно его оси вращения.
и назовем моментом инерции тела относительно его оси вращения. каждой частицы тела на квадрат расстояния
каждой частицы тела на квадрат расстояния  этой частицы до данной оси.
этой частицы до данной оси. .
.
 :
:
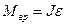 . (1.16.5.)
. (1.16.5.)


