1) Получение нулей в каждой строке, для чего найти наименьший элемент в каждой строке di и вычесть его из всех элементов для образования новой таблицы (Таблица 2). Аналогично делается для каждого столбца (Таблица 3).
Таблица 2.
|
| B1
| B2
| B3
| B4
| ai
|
| A1
|
|
|
|
|
|
| A2
|
|
|
|
|
|
| A3
|
|
|
|
|
|
| A4
|
|
|
|
|
|
| bj
|
|
|
|
|
|
| dj
|
|
|
|
|
|
Таблица 3.
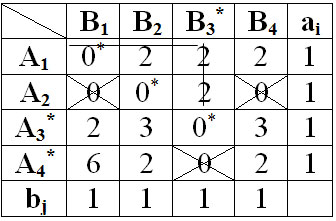
1) Поиск оптимального решения. Для поиска оптимального решения необходимо сначала рассмотреть одну из строк Таблицы 3, имеющую меньшее количество нулей. Отметить "*" один из нулей этой строки и зачеркнуть все остальные нули этой строки и того столбца, в котором находится этот нуль. Аналогичные операции последовательно проводят для всех строк. Если назначения, которые получены при всех нулях, отмечены звездочкой, являются полными (т.е. число нулей со звездочкой равно n), то решение является оптимальным. В противном случае переходят к следующему этапу.
2) Поиск минимального набора строк и столбцов, которые содержат нули. Для этого необходимо отметить звездочкой:
O а) все строки, в которых не имеется ни одного отмеченного "*" нуля.
O б) все столбцы, содержащие перечеркнутый ноль хотя бы в одной из отмеченных "*" строк.
O в) все строки, содержащие отмеченные "*" нули хотя бы в одном из отмеченных "*" столбцов.
Действия б) и в) повторяются поочередно до тех пор, пока есть что отмечать.
После этого необходимо зачеркнуть каждую непомеченную строку, и каждый помеченный столбец.
Цель этого этапа: провести минимальное число горизонтальных и вертикальных прямых, пересекающих, по крайней мере, один раз все нули.
3) Перестановка некоторых нулей: взять наименьшее число из тех клеток, через которые не проведены прямые, вычесть его из каждого числа не вычеркнутых столбцов и прибавить к каждому числу вычеркнутых строк в вычеркнутых столбцах. Получим таблицу 4.
Таблица 4.
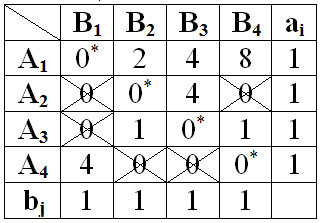
В последней таблице 4 число нулей, отмеченных "*" равно 4=n, следовательно, назначение является полным, а решение оптимальным.
Клетки, отмеченные "*" указывают объект монтажа для каждого крана. Отмеченное решение может быть не единственным. Проверим для данной задачи:
Y = 3+4+2+8 = 17 - общее время монтажа.






