Функции комплексного переменного. Предел и непрерывность функции
В свободное время можно познакомиться с достопримечательностями поселка, поетить музей АРКАИМА или сувенирную лавку., а такжеполюбоваться удивительным закатом в Аркаимской долине. День 3: Ранний подъем 05:00. Встречаем рассвет. Завтрак. Отправление в Пермь. Возвращение в Пермь в воскресенье примерно к 22:00.
Стоимость тура от 6 700 руб./чел. В стоимость входит:трансфер, проживание в домиках (2 ночевки), экскурсионная программа, страховка.
Дополнительно оплачиваются: - горячее питания на ваш вкус и кошелек - услуги гида, подъезд к каждой горе -150 руб./чел.
Заявки по телефонам: 8 912 580 83 76 или через интернет http://vk.com/club68721252 18.09.2015 ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО Функции комплексного переменного. Предел и непрерывность функции Говорят, что на множестве D точек плоскости Например, Мы будем рассматривать только такие функции, для которых множества D и G являются областями, причем D называется областью определения, а G – областью значений функции Определение. Функция Задание функции комплексного переменного
где Это позволяет свести изучение функции комплексного переменного к изучению двух функций действительных переменных. Пример 1. Выделим действительную и мнимую части функции
Отсюда
Геометрически заданную на D однозначную функцию
Точки z, линии Если кривая
Если в плоскости z кривая
Определение. Комплексное число Существование Определение. Функция
|


 задана функция
задана функция  , если каждой точке
, если каждой точке  поставлено в соответствие одно (однозначная функция) или несколько (многозначная функция) значений комплексного переменного
поставлено в соответствие одно (однозначная функция) или несколько (многозначная функция) значений комплексного переменного  .
.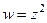 – однозначная функция,
– однозначная функция,  – многозначная функция.
– многозначная функция. .
. , если любым различным значениям
, если любым различным значениям  , взятым из области
, взятым из области  .
. ,
, 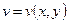 :
: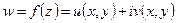 , (1)
, (1) ,
, 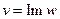 .
. . Так как
. Так как  ,имеем
,имеем .
. ,
,  .●
.●
 , области
, области  называют прообразами точек
называют прообразами точек  и областей
и областей  соответственно, а w,
соответственно, а w,  ,
,  называют образами при отображении
называют образами при отображении  или
или  ,
,  , то можно получить параметрические уравнения
, то можно получить параметрические уравнения 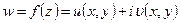 как функции параметра t:
как функции параметра t: .
. , то для нахождения уравнения ее образа
, то для нахождения уравнения ее образа  в плоскости w при отображении, осуществляемом функцией
в плоскости w при отображении, осуществляемом функцией  , достаточно исключить x и y из уравнений
, достаточно исключить x и y из уравнений
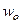 называется пределом функци и
называется пределом функци и 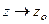 , если для любого
, если для любого  найдется
найдется 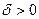 такое, что для всех
такое, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  . В этом случае пишут
. В этом случае пишут  .
. , где
, где  , равносильно существованию
, равносильно существованию  и
и  , причем
, причем  .
. , если она определена в точке
, если она определена в точке  , где
, где  – конечное комплексное число.
– конечное комплексное число.


