где – отрицательно ориентированный замкнутый контур, принадлежащий области аналитичности функции.
При обходе контура Из определения следует, что вычет относительно
Между утверждениями (7) и (2), несмотря на их внешнее сходство, имеется существенное различие. Дело в том, что в разложении Лорана в окрестности точки Пример 4. Найдем вычет функции Лорановское разложение данной функции имеет вид:
Так как коэффициент Теорема 1. (Основная теорема Коши о вычетах). Если функция
Основная теорема о вычетах имеет важное значение для приложений. Она позволяет вычислять интегралы по замкнутому контуру от функции комплексного переменного, не прибегая к первообразным или криволинейным интегралам. С помощью вычетов вычисляются определенные и несобственные интегралы от функций действительного переменного. Пример 5. Вычислим интеграл Простые полюсы
Теорема 2. Если функция
Или
Пример 6. Вычислим интеграл Подынтегральная функция имеет десять простых полюсов
Так как Таким образом
|


 бесконечно удаленная точка
бесконечно удаленная точка  остается слева.
остается слева. равен коэффициенту при
равен коэффициенту при  в лорановском разложении
в лорановском разложении  в окрестности
в окрестности  взятому с противоположным знаком:
взятому с противоположным знаком: (7)
(7)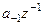 принадлежит правильной (а не главной) части ряда, и
принадлежит правильной (а не главной) части ряда, и  может быть отличным от нуля и тогда, когда
может быть отличным от нуля и тогда, когда  относительно точки
относительно точки  ,
, 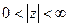
 при
при  равен 1, то
равен 1, то  .
. , за исключением изолированных особых точек
, за исключением изолированных особых точек  то для любого замкнутого контура
то для любого замкнутого контура 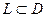 , охватывающего эти точки
, охватывающего эти точки . (8)
. (8) , где
, где 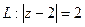 .
. и
и  находятся внутри контура
находятся внутри контура  , поэтому, применяя первую теорему о вычетах можно записать
, поэтому, применяя первую теорему о вычетах можно записать .●
.● (9)
(9)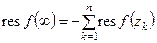 . (10)
. (10)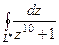 , где
, где 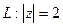 .
. , лежащих на единичной окружности. Лорановское разложение функции в окрестности бесконечно удаленной точки имеет вид
, лежащих на единичной окружности. Лорановское разложение функции в окрестности бесконечно удаленной точки имеет вид ,
,  .
. , то, применяя вторую теорему о вычетах можно записать
, то, применяя вторую теорему о вычетах можно записать  .
. .●
.●


