В зависимости от проведения функции в окрестности особой точки различают три типа особенностей.
Изолированная особая точка  функции
функции  называется:
называется:
а) устранимой особой точкой, если существует конечный предел
 , (1)
, (1)
б) полюсом, если  , (2)
, (2)
причем полюсом  -гопорядка, если
-гопорядка, если
 , (3)
, (3)
и простым полюсом при 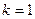 ;
;
в) существенно особой точкой, если не существует  (ни конечный, ни бесконечный).
(ни конечный, ни бесконечный).
Имеют место следующие утверждения:
1. Для того, чтобы изолированная особая точка  функции
функции  была устранимой, необходимо и достаточно, чтобы лорановское разложение
была устранимой, необходимо и достаточно, чтобы лорановское разложение  в окрестности точки
в окрестности точки  не содержало главной части, т.е. имело вид
не содержало главной части, т.е. имело вид
 . (4)
. (4)
2. Для того, чтобы изолированная особая точка  функции
функции  была полюсом
была полюсом  -го порядка, необходимо и достаточно, чтобы главная часть лорановского разложения содержала лишь конечное число
-го порядка, необходимо и достаточно, чтобы главная часть лорановского разложения содержала лишь конечное число  членов
членов
 ,
,  . (5)
. (5)
3. Для того, чтобы изолированная особая точка  функции
функции  была существенно особой, необходимо и достаточно, чтобы главная часть лорановского разложения содержала бесконечно много членов.
была существенно особой, необходимо и достаточно, чтобы главная часть лорановского разложения содержала бесконечно много членов.
Пример 1. Особой точкой функции  является точка
является точка  . Разложение этой функции в ряд Лорана имеет вид:
. Разложение этой функции в ряд Лорана имеет вид:
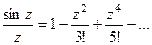
Так как главная часть отсутствует, то  является устранимой особой точкой.
является устранимой особой точкой.
Пример 2. Особой точкой функции  является точка
является точка  . Разложение этой функции в ряд Лорана имеет вид:
. Разложение этой функции в ряд Лорана имеет вид:

Главная часть состоит из двух слагаемых, поэтому  – полюс второго порядка.
– полюс второго порядка.
Пример 3. Особой точкой функции 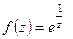 является точка
является точка  . Разложение этой функции в ряд Лорана имеет вид:
. Разложение этой функции в ряд Лорана имеет вид:
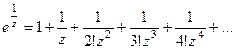
Главная часть разложения бесконечна, поэтому  – существенно особая точка.●
– существенно особая точка.●
Точка  называется нулем функции
называется нулем функции  , если
, если  . Точка
. Точка  называется нулем порядка
называется нулем порядка  , если
, если
 , а
, а  . (6)
. (6)
Ряд Тейлора в окрестности точки  – нуля порядка
– нуля порядка 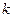 функции
функции  – имеет вид
– имеет вид 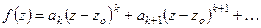
Теорема. Для того, чтобы точка  была нулем порядка
была нулем порядка  функции
функции  , необходимо и достаточно, чтобы имело место равенство
, необходимо и достаточно, чтобы имело место равенство
 ,(7)
,(7)

 функции
функции  называется:
называется: , (1)
, (1) , (2)
, (2) -гопорядка, если
-гопорядка, если , (3)
, (3)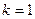 ;
; (ни конечный, ни бесконечный).
(ни конечный, ни бесконечный). . (4)
. (4) была полюсом
была полюсом  членов
членов ,
,  . (5)
. (5) является точка
является точка  . Разложение этой функции в ряд Лорана имеет вид:
. Разложение этой функции в ряд Лорана имеет вид: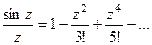
 является точка
является точка 
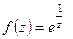 является точка
является точка 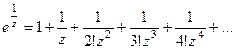
 . Точка
. Точка  , если
, если , а
, а  . (6)
. (6)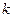 функции
функции  – имеет вид
– имеет вид 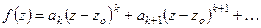
 функции
функции  ,(7)
,(7)


