Для определения порядка нуля функции полезно помнить, что если  нуль порядка
нуль порядка  для
для 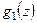 и нуль порядка
и нуль порядка  для
для  , то
, то  – нуль порядка
– нуль порядка 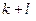 для произведения
для произведения  , порядка
, порядка  (при
(при 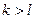 ) для частного
) для частного 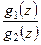 ;
;  – правильная точка, не являющаяся нулем при
– правильная точка, не являющаяся нулем при  и особая точка при
и особая точка при 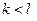 .
.
Теорема. Для того, чтобы точка  была полюсом порядка
была полюсом порядка  для функции
для функции  , необходимо и достаточно, чтобы эта точка была нулем порядка
, необходимо и достаточно, чтобы эта точка была нулем порядка 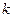 для функции
для функции  .
.
Рассмотрим особенности функции в бесконечно удаленной точке.
Под точкой  понимают абстрактную точку плоскости
понимают абстрактную точку плоскости  , окрестностью которой, является множество чисел
, окрестностью которой, является множество чисел  , удовлетворяющих неравенству
, удовлетворяющих неравенству 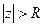 , где
, где 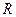 – любое действительное положительное число.
– любое действительное положительное число.
Ряд Лорана функции  в окрестности точки
в окрестности точки  определяют с помощью замены переменной
определяют с помощью замены переменной  для функции
для функции  в окрестности точки
в окрестности точки  . Ряд Лорана в окрестности точки
. Ряд Лорана в окрестности точки  имеет вид
имеет вид
 ,
,
где  главная часть,
главная часть,
 правильная часть.
правильная часть.
Поведение функции в окрестности бесконечно удаленной точки дает возможность классифицировать ее особенности в этой точке.
1. Точка  называется устранимой особой точкой функции, если
называется устранимой особой точкой функции, если  , где
, где 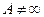 .
.
Ряд Лорана в этом случае не содержит положительных степеней
 .
.
2. Точка  называется полюсом функции, если
называется полюсом функции, если  .
.
Если ряд Лорана в окрестности  содержит конечное число
содержит конечное число  положительных степеней:
положительных степеней:
 ,
,
то точка  называется полюсом порядка
называется полюсом порядка  .
.
3. Точка  называется существенно особой для функции, если
называется существенно особой для функции, если  не существует.
не существует.
Ряд Лорана в этом случае содержит бесконечное число положительных степеней  .
.
Заметим, что точка 
 называется нулем порядка
называется нулем порядка  функции
функции  , если точка
, если точка  является нулем порядка
является нулем порядка  для функции
для функции  .
.

 нуль порядка
нуль порядка  для
для 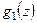 и нуль порядка
и нуль порядка  для
для  , то
, то 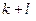 для произведения
для произведения  , порядка
, порядка  (при
(при 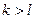 ) для частного
) для частного 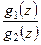 ;
;  и особая точка при
и особая точка при 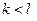 .
. , необходимо и достаточно, чтобы эта точка была нулем порядка
, необходимо и достаточно, чтобы эта точка была нулем порядка 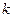 для функции
для функции  .
. понимают абстрактную точку плоскости
понимают абстрактную точку плоскости  , окрестностью которой, является множество чисел
, окрестностью которой, является множество чисел 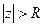 , где
, где 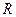 – любое действительное положительное число.
– любое действительное положительное число. в окрестности точки
в окрестности точки  для функции
для функции  в окрестности точки
в окрестности точки  . Ряд Лорана в окрестности точки
. Ряд Лорана в окрестности точки  ,
, главная часть,
главная часть, правильная часть.
правильная часть. называется устранимой особой точкой функции, если
называется устранимой особой точкой функции, если  , где
, где 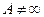 .
. .
. .
. положительных степеней:
положительных степеней: ,
, называется полюсом порядка
называется полюсом порядка  не существует.
не существует.
 функции
функции  , если точка
, если точка  является нулем порядка
является нулем порядка  .
.


