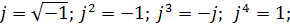Пример решения задачи 2
Выбрав свой вариант задачи 2 по табл. 3 и выписав исходные данные, формулируем конкретное условие задачи. Например: Определить по критериям Гурвица и Михайлова устойчивость САУ, состоящей из трёх последовательно соединённых звеньев А, Е и Ж, третье звено охвачено местной отрицательной обратной связью (четвертым звеном М). САУ охвачена главной отрицательной обратной связью с коэффициентом kгос= -1. 1. Определяем передаточные функции звеньев САУ. Из табл.4 берем исходные данные. Звено 1 - А (безынерционное): y(t)=kx(t); Y1(P)=k1X1(p); W1 (p)=Y1(p)/X1p=k1; k1=10. Звено 2-Е (интегро-дифференцирующее):
Звено 3 - Ж (инерционное 2-го порядка):
Звено 4 - М (звено корректирующей отрицательной обратной связи): y(t)=kКОСx(t);
2. Составляем структурную алгоритмическую схему САУ (рис.4). 3. Определяем передаточную функцию прямой ветви САУ (см.рис.4): Wn(p) = W1(p) W2(p) W3кос(p), где передаточная функция третьего звена, охваченного корректирующей (местной) отрицательной обратной связью, определяется в виде: W3кос = W3(p)/[1 + W3(p) Wкос(p)]. Подставляя соответствующие выражения передаточных функций звеньев с учетом численных значений коэффициентов kt и постоянных времени Ti получим:
4. Определяем передаточную функцию замкнутой САУ:
5. Вычисляем характеристическое уравнение замкнутой САУ G(p)=0:
Подставляя значения передаточных функций G(p)=5p311p2+107p+85=0.
Рис 4 Структурная алгоритмическая схема САУ (к задаче 2).
Рис.5 - Годограф Михайлова САУ (к задаче 2). 6. Определяем устойчивость по критерию Гурвица. Исследуемая САУ имеет характеристическое уравнение 3-й степени: а0р +a1p2+a2p+a3=0 Матрица Гурвица будет иметь вид:
Поскольку все коэффициенты характеристического уравнения положительны а0=5>0; a1=11>0; а2=107>0; а3=85>0 и определитель ∆2=a1a2 - а0а3=11·107-85·5=752>0, то исследуемая САУ устойчива. 7. Определяем устойчивость по критерию Михайлова. Для полученного характеристического уравнения комплексный многочлен имеет вид: G(jω)=5(jω)3+11(jω)2+107jω+85. Разделим многочлен G(jω) на действительную Re[G(jω)] и мнимую Im[G(jω)] части: G(jω)=Re[G(jω)] +Im[G(jω)] =R(ω) +jJ(ω), имея ввиду, что G(jω)=85-11ω2+ jω(107-5 ω2)= R(ω)+Jj(ω). Задаваясь различными значениями частоты ω, найдем координаты R(ω) и J(ω) точек годографа Михайлова. Вначале находим значения для характерных точек (при J(ω))=0 и при R(ω)=0). Годограф пересекает ось абсцисс, если J(ω)=ω (107-5ω2)=0. Решение этого уравнения дает действительные корни: ω1=0; ω2=4,6. Находим значения ω, при которых годограф пересекает ось ординат: R(ω)=85-11ω2=0. Это уравнение имеет один действительный корень ω3=2,78. Задаваясь несколькими промежуточными значениями частоты ω, вычисляем значения R(ω) и J(ω). Результаты сводим в табл. 5
Таблица 5 Координаты точек годографа Михайлова
По полученным точкам строим годограф Михайлова (рис.5). Так как при изменении частоты от 0 до ∞ годограф Михайлова, вращаясь в положительном направлении против часовой стрелки, начинается на положительной части вещественной оси, последовательно проходит три квадранта и не пересекает начала координат, то анализируемая система третьего порядка устойчива. Вывод. Проверка по двум критериям (Гурвица и Михайлова) показала, что исследуемая САУ устойчива.
Литература 1. Бородин И.Ф., Недилько Н.М. Автоматизация технологических процессов. - М.:Агропромиздат, 1986. 2. Бородин И.Ф., Кирилин Н.И. Основы автоматики и автоматизации производственных процессов, - М.:Колос, 1977. 3. Автоматика и автоматизация производственных процессов: Учебное пособие/Под ред.И.И. Мартыненко. - М.:Агропромиздат, 1986. 4. Бохан Н.И., Бородин И.Ф. и др. Технические средства автоматики и телемеханики. - М.:Агропромиздат, 1992. 5. Бородин И.Ф. Технические средства автоматики. - М.:Колос, 1982. 6. Элементы и устройства сельскохозяйственной автоматики.:Справоч. пособие /Под ред. Н.И. Бохана. - Минск. 1983. 7. Яницкий С.В. Применение электроэнергии и основы автоматизации производственных процессов. - М.:Колос, 1977.
|

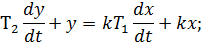



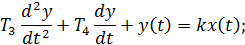
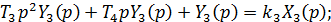





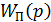 и
и 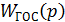 , получим после преобразований:
, получим после преобразований: