Энтропия и ее свойства.
Энтропия источника. Основной характеристикой источника информации является его энтропия, равная среднему количеству информации, приходящейся на одно состояние источника. Это значит, что, узнав о реализации (наступлении) какого-либо из состояний источника, мы получаем информацию, равную по количеству энтропии этого источника. Энтропия отражает степень неопределенности состояния системы и одновременно является количественной мерой информации. Свойство 1. Энтропия является неотрицательной ограниченной функцией, определенной на отрезке от 0 до 1. Это следует из того, что для pi (0 ≤ pi ≤ 1) функция log2 pi ≤ 0, а значит, слагаемые hi = – pilog2 pi (1 ≤ i ≤ N) неотрицательны. Чтобы убедиться в том, что функция ограничена, найдем предел hi при pi → 0:
Таким образом, H ( Свойство 2. Энтропия является монотонно возрастающей функцией от числа состояний N, если все состояния равновероятны. Для доказательства этого свойства покажем, что при
Как известно, логарифм является монотонно возрастающей функцией своего аргумента, в данном случае N. Свойство 3. Энтропия равна 0 лишь в том случае, когда вероятность одного из состояний равна 1, а вероятности остальных состояний нулевые. Эта ситуация возникает тогда, когда заведомо известен исход события, т. е. N = 1, что является не уменьшаемым значением информационной неопределенности, не связанным с получением информации. Свойство 4. Энтропия максимальна, когда все состояния источника равновероятны. Этот случай соответствует максимальной неопределенности состояния источника (непредсказуемости возможного исхода). Свойство 5. Энтропия не зависит от пути выбора состояния источника. Выбор может быть как непосредственным, так и многоступенчатым. В последнем случае неопределенность выбора состояния складывается из неопределенностей выбора группы состояний и неопределенностей выбора состояния в каждой группе. Свойство 6. Энтропия обладает свойством аддитивности. Смысл этого свойства заключается в следующем. Если два источника U и V независимо друг от друга принимают состояния ( Завершая изучение основных свойств энтропии, отметим следующий факт. Доказано, что функционал вида
|


 ) ≥ 0 и ограничена.
) ≥ 0 и ограничена. формула Шеннона переходит в формулу Хартли:
формула Шеннона переходит в формулу Хартли: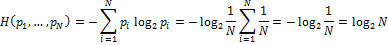
 ) и (
) и ( соответственно, то их можно рассматривать как один источник UV, состояния которого определяются парами (
соответственно, то их можно рассматривать как один источник UV, состояния которого определяются парами ( )при i= 1,…, N; j = 1,…, M. В этом случае H(UV) = H(U) + H(V).
)при i= 1,…, N; j = 1,…, M. В этом случае H(UV) = H(U) + H(V).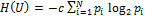 является единственным, удовлетворяющим всем сформулированным выше свойствам. Здесь c –некоторая константа. В нашем случае c = 1.
является единственным, удовлетворяющим всем сформулированным выше свойствам. Здесь c –некоторая константа. В нашем случае c = 1.


