Методы построения оптимальных кодов
Оптимальное кодирование - ко дирование, минимизирующее избыточность кода. Оптимальный код, как правило, неравномерный. Рассмотрим два наиболее известных метода оптимального побуквенного кодирования. Метод Шеннона – Фано: Шаг 1. Упорядочиваем символы исходного алфавита в порядке невозрастания их вероятностей. (Записываем их в строку.) Шаг 2. Не меняя порядка символов, делим их на две группы так, чтобы суммарные вероятности символов в группах были по возможности равны. Шаг 3. Приписываем группе слева "0", а группе справа "1" в качестве элементов их кодов. Шаг 4. Просматриваем группы. Если число элементов в группе более одного, идем на Шаг 2. Если в группе один элемент, построение кода для него завершено. Очевидно, что процесс построения кода в общем случае содержит неоднозначность, так как мы не всегда можем поделить последовательность на два равновероятных подмножества. Либо слева, либо справа сумма вероятностей будет больше. Критерием лучшего варианта является меньшая избыточность кода. Заметим также, что правильное считывание кода – от корня дерева к символу, – обеспечит его префиксность. Метод Хаффмана: Шаг 1. Упорядочиваем символы исходного алфавита в порядке невозрастания их вероятностей. (Записываем их в столбец). Шаг 2. Объединяем два символа с наименьшими вероятностями. Символу с большей вероятностью приписываем "1", символу с меньшей – "0" в качестве элементов их кодов. Шаг 3. Считаем объединение символов за один символ с вероятностью, равной сумме вероятностей объединенных символов. Шаг 4. Возвращаемся на Шаг 2 до тех пор, пока все символы не будут объединены в один с вероятностью, равной единице. Считывание кода идет от корня двоичного дерева к его вершинам с обозначением символов. Это обеспечивает префиксность кода. Метод Хаффмана также содержит неоднозначность, так как в алфавите могут оказаться несколько символов с одинаковой вероятностью, и код будет зависеть от того, какие символы мы будем объединять в первую очередь. Блочное кодирование. В отличие от побуквенного, блочное кодирование формирует коды для буквосочетаний, составленных из m символов исходного алфавита. Буквосочетания можно рассматривать как новый, расширенный алфавит объемом Блочное кодирование применяется к алфавитам, в которых вероятность появления одной какой-то буквы значительно превышает вероятность появления других букв. Из теории вероятностей известно, что если буквы появляются независимо одна от другой, то вероятность появления некоторой последовательности букв равна произведению вероятностей входящих в нее букв. Исходя из этого, рассчитываем вероятности для буквосочетаний и кодируем их одним из методов побуквенного оптимального кодирования (т. е. методом Шеннона – Фано или методом Хаффмана). Однако практика показывает, что с увеличением числа символов в блоке больше четырех, сложность кодирующего устройства растет быстрее, чем оптимальность кода. Поэтому применение слишком длинных блоков нецелесообразно.
|

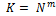 , где N – объем исходного алфавита; m – число символов в буквосочетании.
, где N – объем исходного алфавита; m – число символов в буквосочетании.


