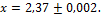Поскольку все числа в ЭВМ записываются в конечную разрядную сетку, очень актуальна процедура округления числа до требуемого количества разрядов.
Округлением числа  до
до  разрядов в заданной системе счисления называется операция замены его таким числом xs, все разряды которого, начиная с
разрядов в заданной системе счисления называется операция замены его таким числом xs, все разряды которого, начиная с  го и младше, равны нулю.
го и младше, равны нулю.
Простейшая процедура округления заключается в "отбрасывании" разрядов, начиная с 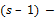 го. Таким образом, если число x имеет вид
го. Таким образом, если число x имеет вид  то
то 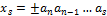
Разность между округлённым и округляемым значениями называется ошибкой (погрешностью) округления:

Очевидно, что при таком способе округления (назовём его первым) ошибка всегда будет иметь знак, противоположный знаку округляемого числа. Это может приводить к быстрому накоплению ошибки в вычислениях.
Давайте оценим ошибку по величине. Абсолютная погрешность округления  имеет наибольшее значение, когда числа
имеет наибольшее значение, когда числа  и т. д. принимают наибольшее значение, равное максимальному базисному числу в рассматриваемой системе счисления с основанием p:
и т. д. принимают наибольшее значение, равное максимальному базисному числу в рассматриваемой системе счисления с основанием p: 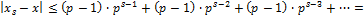
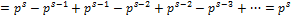
Итак, верхняя оценка для абсолютной погрешности получилась равной 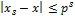
Но процесс округления 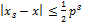 является лучшим, так как он обеспечивает наименьшую погрешность округления, так как знак ошибки округления будет меняться (в половине случаев округление идет с недостатком, а в половине - с избытком.) Поэтому накопление ошибки в арифметических действиях не будет происходить заведомо быстро.
является лучшим, так как он обеспечивает наименьшую погрешность округления, так как знак ошибки округления будет меняться (в половине случаев округление идет с недостатком, а в половине - с избытком.) Поэтому накопление ошибки в арифметических действиях не будет происходить заведомо быстро.
Выразим данную процедуру округления формально. Числа, имеющие нулевые разряды, начиная с 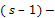 го, образуют на вещественной оси равномерную сетку с шагом
го, образуют на вещественной оси равномерную сетку с шагом 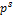 . Среди них есть число
. Среди них есть число  , наиболее близкое к
, наиболее близкое к  . Ясно, что
. Ясно, что 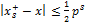
Из геометрических соображений следует, что наилучшее приближение  к x будет единственным, если имеет место строгое неравенство. Учитывая возможность равенства, запишем
к x будет единственным, если имеет место строгое неравенство. Учитывая возможность равенства, запишем
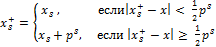 (2)
(2)
где  – округление отбрасыванием разрядов;
– округление отбрасыванием разрядов;  – наилучшее округление;
– наилучшее округление; 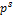 – единица
– единица  –го разряда.
–го разряда.
Этот способ округления идентичен принятому в 10-ичной системе счисления. В машинах он реализуется в два этапа: 1) к старшему из отбрасываемых разрядов, 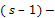 му, прибавляем
му, прибавляем  ; 2) разряды с
; 2) разряды с 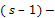 го отбрасываются.
го отбрасываются.
Округление числа до верной цифры: Числа, представляющие собой результат вычислений или измерений, как правило, содержат ошибку и в общем случае их принято записывать в виде 
где  – приближенное значение числа
– приближенное значение числа  ;
;  – абсолютная погрешность этого приближения.
– абсолютная погрешность этого приближения.
В соответствии с требованиями теории погрешностей все цифры числа  должны быть верными. Приведем определение.
должны быть верными. Приведем определение.
Цифра  в записи
в записи  - ичной дроби приближенного числа
- ичной дроби приближенного числа  называется верной, если погрешность приближения не превышает единицы
называется верной, если погрешность приближения не превышает единицы  - го разряда.
- го разряда.
Например, рассмотрим запись  . Цифры 2, 3, 6 являются верными, так как выполняются неравенства
. Цифры 2, 3, 6 являются верными, так как выполняются неравенства  а цифра 5 является сомнительной, поскольку единица разряда, в котором она записана, меньше погрешности
а цифра 5 является сомнительной, поскольку единица разряда, в котором она записана, меньше погрешности 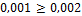 .
.
В подобных случаях требуется округление числа a до верной s -й цифры  . При этом ошибка округления суммируется с исходной абсолютной погрешностью числа
. При этом ошибка округления суммируется с исходной абсолютной погрешностью числа  . Пусть, начиная с (s – 1)-го разряда, все цифры числа a являются сомнительными. Обозначим сомнительную часть числа
. Пусть, начиная с (s – 1)-го разряда, все цифры числа a являются сомнительными. Обозначим сомнительную часть числа  . Тогда алгоритм округления до верной s -й цифры имеет вид
. Тогда алгоритм округления до верной s -й цифры имеет вид
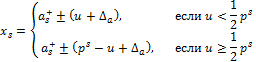
где 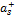 – это число a, округленное в соответствии с (2). Так, рассмотренное нами число
– это число a, округленное в соответствии с (2). Так, рассмотренное нами число  после процедуры округления его до верной цифры правильнее будет записать как
после процедуры округления его до верной цифры правильнее будет записать как 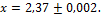

 до
до  разрядов в заданной системе счисления называется операция замены его таким числом xs, все разряды которого, начиная с
разрядов в заданной системе счисления называется операция замены его таким числом xs, все разряды которого, начиная с  го и младше, равны нулю.
го и младше, равны нулю.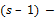 го. Таким образом, если число x имеет вид
го. Таким образом, если число x имеет вид  то
то 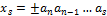

 имеет наибольшее значение, когда числа
имеет наибольшее значение, когда числа  и т. д. принимают наибольшее значение, равное максимальному базисному числу в рассматриваемой системе счисления с основанием p:
и т. д. принимают наибольшее значение, равное максимальному базисному числу в рассматриваемой системе счисления с основанием p: 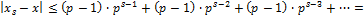
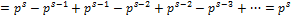
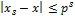
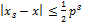 является лучшим, так как он обеспечивает наименьшую погрешность округления, так как знак ошибки округления будет меняться (в половине случаев округление идет с недостатком, а в половине - с избытком.) Поэтому накопление ошибки в арифметических действиях не будет происходить заведомо быстро.
является лучшим, так как он обеспечивает наименьшую погрешность округления, так как знак ошибки округления будет меняться (в половине случаев округление идет с недостатком, а в половине - с избытком.) Поэтому накопление ошибки в арифметических действиях не будет происходить заведомо быстро.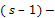 го, образуют на вещественной оси равномерную сетку с шагом
го, образуют на вещественной оси равномерную сетку с шагом 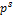 . Среди них есть число
. Среди них есть число  , наиболее близкое к
, наиболее близкое к 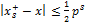
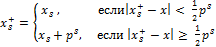 (2)
(2) – округление отбрасыванием разрядов;
– округление отбрасыванием разрядов;  ; 2) разряды с
; 2) разряды с 
 – приближенное значение числа
– приближенное значение числа  – абсолютная погрешность этого приближения.
– абсолютная погрешность этого приближения. в записи
в записи  - ичной дроби приближенного числа
- ичной дроби приближенного числа  - го разряда.
- го разряда. . Цифры 2, 3, 6 являются верными, так как выполняются неравенства
. Цифры 2, 3, 6 являются верными, так как выполняются неравенства  а цифра 5 является сомнительной, поскольку единица разряда, в котором она записана, меньше погрешности
а цифра 5 является сомнительной, поскольку единица разряда, в котором она записана, меньше погрешности 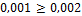 .
. . При этом ошибка округления суммируется с исходной абсолютной погрешностью числа
. При этом ошибка округления суммируется с исходной абсолютной погрешностью числа  . Тогда алгоритм округления до верной s -й цифры имеет вид
. Тогда алгоритм округления до верной s -й цифры имеет вид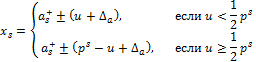
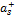 – это число a, округленное в соответствии с (2). Так, рассмотренное нами число
– это число a, округленное в соответствии с (2). Так, рассмотренное нами число  после процедуры округления его до верной цифры правильнее будет записать как
после процедуры округления его до верной цифры правильнее будет записать как