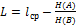Количество и объем информации. Избыточность кода.
Рассмотрим схему обращения информации Отправитель передал сообщение, состоящее из m букв алфавита A, обладающего энтропией H(A). Количество информации в сообщении равно Кодирующее устройство кодирует исходное сообщение символами алфавита B с энтропией H(A). Если код равномерный, то количество информации в закодированном сообщении
Сравним полученные значения I и Ik.Ясно, что в общем случае Однако, в соответствии с определением, кодирование есть переход от одной формы записи к другой, содержащей ту же самую информацию. И с этой точки зрения неравенство Объёмом информации – кол-о перед-ой инф-ии, рассчитанное относительно кодового (вторичного) алфавита При неравномерном кодировании объём информации выражается по формуле Mинимально возможная средняя длина кодового слова равна Cредняя длина кодового слова при кодировании произвольного алфавита A любым двоичным кодом не может быть меньше энтропии исходного алфавита. Избыточностью кода - превышение средней длины кода над минимально возможной Избыточность кода является следствием как процедуры кодирования (природы кода), так и свойств алфавитов, в этом процессе участвующих.
|
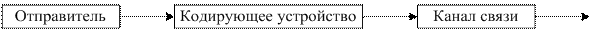
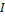=m 
H(A)
легко подсчитать: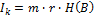
где r – разрядность равномерного кода.
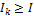. Это следует из формулы расчета минимальной разрядности кода. Равенство имеет место лишь в весьма редких случаях. Например, при двоичном кодировании равновероятного алфавита А, если при этом 
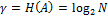, и H (B) = 1.
.
.
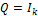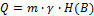
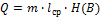
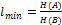