Диапазоны представимых чисел в форме с фиксированной и плавающей запятой.
Начнём с разрядной сетки типа ФЗ,
Его можно выразить как
Объединив полученные результаты, запишем диапазон: Для произвольной натуральной системы счисления с основанием p: Все числа все числа Рассуждая аналогично, найдём диапазон чисел в разрядной сетке типа ФЗ, б: Чтобы произвольное число х поместилось в разрядную сетку, в общем случае его предварительно следует отмасштабировать, т. е. домножить на число Необходимость ручного масштабирования является одним из основных недостатков разрядных сеток такого типа, ограничивая их применение в вычислительных машинах. Кроме того, относительная погрешность малых чисел оказывается очень высока при таком способе их записи. Поэтому на практике большее применение получили разрядные сетки с плавающей запятой, в которых размещается не только само число, но и его масштаб. Диапазон представимых чисел для разрядных сеток с плавающей запятой значительно шире, чем для сеток с фиксированной запятой. Для положительных чисел получаем: наибольшее
Для отрицательных чисел:
Объединяем интервалы: Этот результат получен для 2-ичной СС, но его легко обобщить для произвольной натуральной СС с основанием
Отсюда видно, что чем больше Область машинного нуля имеет вид Область переполнения Итак, представление числа с плавающей запятой имеет ряд преимуществ: – шире диапазон представимых чисел; – не требуется предварительное масштабирование чисел; – относительная погрешность числа не зависит от его значения.
|

 Для того что бы найти диапазон чисел, представимых в разрядных сетках с фиксированной запятой надо найти наибольшее и наименьшее значение чисел для положительной и отрицательной частей числовой оси.
Для того что бы найти диапазон чисел, представимых в разрядных сетках с фиксированной запятой надо найти наибольшее и наименьшее значение чисел для положительной и отрицательной частей числовой оси. а. Для простоты рассмотрим случай
а. Для простоты рассмотрим случай  . Наибольшее положительное число в разрядной сетке будет иметь вид:
. Наибольшее положительное число в разрядной сетке будет иметь вид: , где
, где  – число разрядов, отведённых под запись числа.
– число разрядов, отведённых под запись числа.





 образуют область машинного нуля, попадая в которую число считается равным нулю;
образуют область машинного нуля, попадая в которую число считается равным нулю; образуют область переполнения - если в процессе вычислений промежуточный результат попадает в эту область, то следует аварийная остановка вычислительного процесса.
образуют область переполнения - если в процессе вычислений промежуточный результат попадает в эту область, то следует аварийная остановка вычислительного процесса.
 – масштаб, такое, чтобы результат
– масштаб, такое, чтобы результат 
 или
или 
 или
или 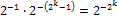





 :
:
 и
и  , тем шире диапазон представимых чисел.
, тем шире диапазон представимых чисел. она зависит только от
она зависит только от 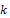 – числа разрядов, отведённых под порядок.
– числа разрядов, отведённых под порядок.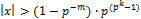 определяется всеми параметрами сетки.
определяется всеми параметрами сетки.


