Систематический и несистематический риски. Модель САРМ.
Общий риск портфеля состоит из двух частей: диверсифицируемый (несистематический) риск, т.е. риск, который может быть элиминирован за счет диверсификации (инвестирование 1 млн. руб. в акции десяти компаний менее рискованно, нежели инвестирование той же суммы в акции одной компании); недиверсифицируемый (систематический, или рыночный) риск, т.е. риск, который нельзя уменьшить путем изменения структуры портфеля. Пороговая ставка доходности - мин ставка на котор согласен инвестор iпор=RF+RP, RF-безриск ставка RP-плата за риск. Для определения RP используют оценку капитальных активов САРМ. iпор=RF+(E(R)м – RF)*β, E(R)м-среднерыночная доходность, β- коэф дает конкретность. (из лекции)
Имея в виду, что переменная х представляет собой риск, характеризуемый показателем ß, а у — ожидаемую доходность ke, получим следующую формулу, которая и является моделью САРМ: ke = krf + ß · (km – krf), где ke — ожидаемая доходность акций данной компании; krf — доходность безрисковых ценных бумаг (в частности, в США берут за основу государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка) km — ожидаемая доходность в среднем на рынке ценных бумаг; ß — бета-коэффициент данной компании. Показатель (km—krf) имеет вполне наглядную интерпретацию, представляя собой рыночную (т.е. в среднем) премию за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпораций и пр.). Аналогично, показатель (kg—krf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компании. Модель САРМ означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск.
|

 Для понимания логики модели легче всего воспользоваться графическим представлением (рис. 5.12). Ставится задача найти взаимосвязь между ожидаемой доходностью (у) и риском ценной бумаги (х), т.е. построить функцию у = f(x). Построение основывается на следующих очевидных рассуждениях: а) доходность ценной бумаги связана с присущим ей риском прямой связью; б) риск характеризуется некоторым показателем ß; в) «средней» ценной бумаге т.е. бумаге, имеющей средние значения риска и доходности, соответствуют ß = 1 и доходность km; г) имеются доходности, денные бумаги со ставкой krf и ß = 0. Исходя из приведенных выше предпосылок, доказывается, что искомая зависимость у = f(x) представляет собой прямую линию. Итак, мы имеем две точки с координатами (0, krf) и (1, km). Из курса геометрии известно, что уравнение прямой, проходящей через точки (х1, у1) и (х2, у2) задается формулой:
Для понимания логики модели легче всего воспользоваться графическим представлением (рис. 5.12). Ставится задача найти взаимосвязь между ожидаемой доходностью (у) и риском ценной бумаги (х), т.е. построить функцию у = f(x). Построение основывается на следующих очевидных рассуждениях: а) доходность ценной бумаги связана с присущим ей риском прямой связью; б) риск характеризуется некоторым показателем ß; в) «средней» ценной бумаге т.е. бумаге, имеющей средние значения риска и доходности, соответствуют ß = 1 и доходность km; г) имеются доходности, денные бумаги со ставкой krf и ß = 0. Исходя из приведенных выше предпосылок, доказывается, что искомая зависимость у = f(x) представляет собой прямую линию. Итак, мы имеем две точки с координатами (0, krf) и (1, km). Из курса геометрии известно, что уравнение прямой, проходящей через точки (х1, у1) и (х2, у2) задается формулой: 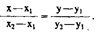 Подставляя в формулу исходные данные, получим: у = krf + (km— krf) · х.
Подставляя в формулу исходные данные, получим: у = krf + (km— krf) · х.


