Необходимое условие экстремума функции двух переменных
Теорема Если функция Доказательство 1. Докажем что равна нулю частная производная по переменной 2. Для этого рассмотрим в окрестности точки 3. Тогда функция 4. Для функции одной переменной выполняется необходимое условие экстремума функции одной переменной: 5. Аналогично функцию Определение 1. Внутренние точки окрестности точки
называются стационарными точками функции Определение 2. Подозрительные на локальный экстремум являются критические точки, в которых хотя бы одна из частных производных №13 Неопределенный интеграл, основные теоремы. Определение: совокупность всех первообразных у=f(х) на промежутке Х, называется неопределенным интегралом. Основные теоремы: — производная от неопределенного интеграла равна подынтегральной функции — дифференциалом неопределенного интеграла является подынтегральное выражение — неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до последнего слагаемого — постоянный множитель можно выносить за знак интеграла — интеграл от алгебраической суммы равен сумме интегралов — интеграл от произведения равен произведению интегралов — интеграл от частного равен частному интегралов — — Совокупность всех первообразных для функции f (х) на промежутке Х называется неопределенным интегралом от функции f (х) и обозначается ò f (х) dx, где ò - знак интеграла, f (х) – подынтегральная функция, f (х) dx – подынтегральное выражение. Производная от неопределенного интеграла равна подынтегральной функции, т.е. (ò f (х) dx) ¢= f (х). Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. d (ò f (х) dx) = f (х) dх.
|
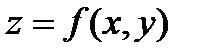имеет в точке 
экстремум, и в этой точке 
существуют частные производные первого порядка, то в этой точке 
частные производные первого порядка равны 0, т.е. 
.
в точке 
, если 
– точка экстремума функции.
, т.е. 
фиксируем.
может быть рассмотрена как функция одной переменной 
, которая имеет экстремум в точке 
и имеет производную 
.
.
можно рассмотреть как функцию одной переменной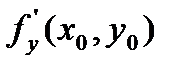 
в точке 
. ч.т.д.
,
для любой упорядоченной пары 
из 
- окрестности точки 
. 
, 
не существует или если они обе существуют, то равны нулю[1].
