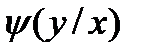Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, даются формуламиM(X) = np, D(X) = npq. — Следствие. Математическое ожидание величины (m/n) в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. M(m/n) = р, D(m /n)=pq/n. — Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0,1 2,…,m,…,n с вероятностями р(m) = Р(Х=m) =е─λ λm/m!, где λ = np. Tеорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона. т.е. М(Х) = λ, D(X)= λ;. Распределение Пуассона ─ частный случай биномиального закона распределения для относительно больших n и относительно малых р. — Равномерный закон распределения Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если её плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.e. —
№48 Числовые характеристики системы двух случайных величин
— — — где - условная плотность случайной величины Y при X=x.
|
Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и s2, если её плотность вероятности имеет вид:
Условным математическим ожиданием дискретной случайной величины Y при X=x (x- определенное возможное значение X) называют сумму произведений возможных значений Y на их условные вероятности: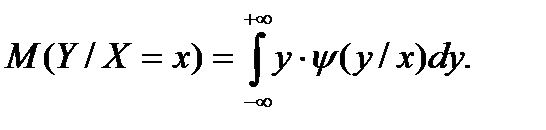
Для непрерывных величин:
