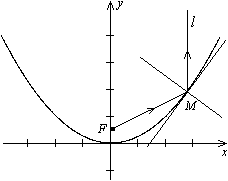Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса  опустим перпендикуляр
опустим перпендикуляр  на директрису
на директрису  . Начало координат
. Начало координат  расположим на середине отрезка
расположим на середине отрезка  , ось
, ось  направим вдоль отрезка
направим вдоль отрезка  так, чтобы ее направление совпадало с направлением вектора
так, чтобы ее направление совпадало с направлением вектора 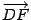 . Ось
. Ось  проведем перпендикулярно оси
проведем перпендикулярно оси  (рис. 12.15).
(рис. 12.15).
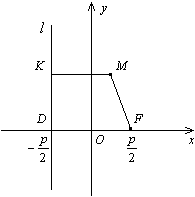
Рис.12.15.
Теорема 12.4 Пусть расстояние между фокусом  и директрисой
и директрисой  параболы равно
параболы равно  . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение

| (12.10)
|
Доказательство. В выбранной системе координат фокусом параболы служит точка  , а директриса имеет уравнение
, а директриса имеет уравнение  (рис. 12.15).
(рис. 12.15).
Пусть  -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
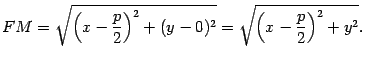
Расстоянием от точки  до директрисы
до директрисы  служит длина перпендикуляра
служит длина перпендикуляра  , опущенного на директрису из точки
, опущенного на директрису из точки  . Из рисунка 12.15 очевидно, что
. Из рисунка 12.15 очевидно, что  . Тогда по определению параболы
. Тогда по определению параболы  , то есть
, то есть

Возведем обе части последнего уравнения в квадрат:
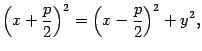
откуда
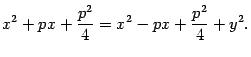
После приведения подобных членов получим уравнение (12.10).
Уравнение (12.10) называется каноническим уравнением параболы.
Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью  .
.
Доказательство. Проводится так же, как и доказательство (предложения 12.1).
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если переобозначить переменные  ,
,  , то уравнение (12.10) можно записать в виде
, то уравнение (12.10) можно записать в виде
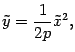
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).

Рис.12.16.Парабола
Пример 12.6 Постройте параболу 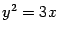 . Найдите ее фокус и директрису.
. Найдите ее фокус и директрису.
Решение. Уравнение является каноническим уравнением параболы,  ,
,  . Осью параболы служит ось
. Осью параболы служит ось  , вершина находится в начале координат, ветви параболы направлены вдоль оси
, вершина находится в начале координат, ветви параболы направлены вдоль оси  . Для построения найдем несколько точек параболы. Для этого придаем значения переменному
. Для построения найдем несколько точек параболы. Для этого придаем значения переменному  и находим значения
и находим значения  . Возьмем точки
. Возьмем точки  ,
, 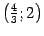 ,
,  . Учитывая симметрию относительно оси
. Учитывая симметрию относительно оси  , рисуем кривую (рис. 12.17)
, рисуем кривую (рис. 12.17)
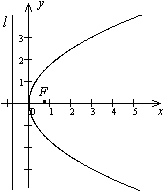
Рис.12.17.Парабола, заданная уравнением 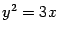
Фокус  лежит на оси
лежит на оси  на расстоянии
на расстоянии  от вершины, то есть имеет координаты
от вершины, то есть имеет координаты  . Директриса
. Директриса  имеет уравнение
имеет уравнение  , то есть
, то есть  .
.
Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.
Предложение 12.5 Пусть  -- фокус параболы,
-- фокус параболы,  -- произвольная точка параболы,
-- произвольная точка параболы,  -- луч с началом в точке
-- луч с началом в точке  параллельный оси параболы. Тогда нормаль к параболе в точке
параллельный оси параболы. Тогда нормаль к параболе в точке  делит угол, образованный отрезком
делит угол, образованный отрезком  и лучом
и лучом  , пополам.
, пополам.
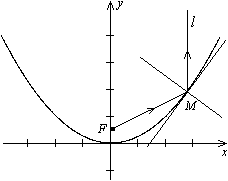
Рис.12.18.Отражение светового луча от параболы
Это свойство означает, что луч света, вышедший из фокуса  , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.
, отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.

 опустим перпендикуляр
опустим перпендикуляр  на директрису
на директрису  . Начало координат
. Начало координат  расположим на середине отрезка
расположим на середине отрезка  направим вдоль отрезка
направим вдоль отрезка 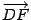 . Ось
. Ось  проведем перпендикулярно оси
проведем перпендикулярно оси 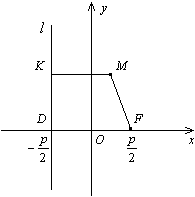
 . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение
 , а директриса имеет уравнение
, а директриса имеет уравнение  (рис. 12.15).
(рис. 12.15). -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим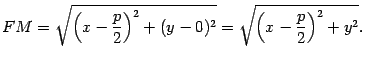
 до директрисы
до директрисы  , опущенного на директрису из точки
, опущенного на директрису из точки  . Тогда по определению параболы
. Тогда по определению параболы  , то есть
, то есть
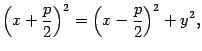
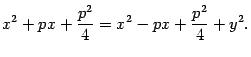
 ,
,  , то уравнение (12.10) можно записать в виде
, то уравнение (12.10) можно записать в виде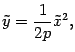

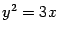 . Найдите ее фокус и директрису.
. Найдите ее фокус и директрису. ,
,  . Осью параболы служит ось
. Осью параболы служит ось  и находим значения
и находим значения  . Возьмем точки
. Возьмем точки  ,
, 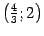 ,
,  . Учитывая симметрию относительно оси
. Учитывая симметрию относительно оси 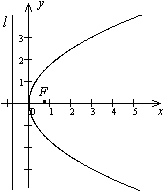
 от вершины, то есть имеет координаты
от вершины, то есть имеет координаты  . Директриса
. Директриса  .
. и лучом
и лучом