РАЗЛИЧНЫЕ УРАВНЕНИЯ ПРЯМОЙ
Прямую в пространстве можно задать различными способами (точкой и вектором, параллельной ей; двумя точками и т. п.), в связи с чем рассматривают различные виды ее уравнений. Векторно-параметрическое уравнение прямой. Направляющим вектором прямой называется любой ненулевой вектор, параллельный ей. Если даны точка
Где
Параметрические уравнения прямой. Переходя от векторного соотношения (4.18) к координатным, получаем
Эти уравнения называются параметрическими уравнениями прямой, проходящей через точку Канонические уравнения прямой. Выражая параметр t из уравнений (4.19) н приравнивая полученные выражения, находим, что
Уравнения (4.20) называются каноническими уравнениями прямой, проходящей через точку Уравнение прямой, проходящей через две точки. Если даны две точки
Взять вектор Поэтому уравнения (4.20) примут вид
Пример 4.10. Записать параметрические и канонические уравнения прямой, проходящей через точку
Так как в данном случае Параметрические уравнения (4Л 9) принимают вид
Пример 4.11. Составить уравнения прямой; проходящей через точки Поскольку
Обозначая равные отношения буквой
|

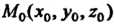 И. направляющий вектор
И. направляющий вектор  Прямой (рис. 4.8), то
Прямой (рис. 4.8), то (4.18)
(4.18) - радиус-вектор точки
- радиус-вектор точки 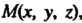
 - радиус-вектор точки
- радиус-вектор точки - переменная величина (параметр). Уравнение (4.18) называется векторно-параметрическим уравнением прямой, проходящей через точку
- переменная величина (параметр). Уравнение (4.18) называется векторно-параметрическим уравнением прямой, проходящей через точку  И имеющей направляющий вектор
И имеющей направляющий вектор  . Равенство (4.18) следует из определения суммы векторов и необходимого и достаточного условия коллинеарности двух векторов.
. Равенство (4.18) следует из определения суммы векторов и необходимого и достаточного условия коллинеарности двух векторов. (4.19)
(4.19) Н имеющей направляющий вектор
Н имеющей направляющий вектор 
 (4.20)
(4.20) И имеющей направляющий вектор
И имеющей направляющий вектор 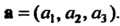
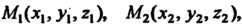 То в качестве ее направляющего вектора можно
То в качестве ее направляющего вектора можно
 (4.21)
(4.21) Параллельно вектору
Параллельно вектору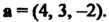


 а канонические уравнения (4.20) запишутся так:
а канонические уравнения (4.20) запишутся так:
 Привести эти уравнения к параметрическому виду. ¦
Привести эти уравнения к параметрическому виду. ¦ , то уравнения (4.21) примут вид
, то уравнения (4.21) примут вид , или
, или 
 Получаем параметрические уравнения данной прямой:
Получаем параметрические уравнения данной прямой:



