Как определить взаимное расположение двух прямых?
Начнём с первого случая: Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства Рассмотрим прямые Действительно, если все коэффициенты уравнения Второй случай, когда прямые параллельны: Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных В качестве примера рассмотрим две прямые Однако совершенно очевидно, что Вывод: И третий случай, когда прямые пересекаются: Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных Так, для прямых Из первого уравнения следует, что Вывод: прямые пересекаются В практических задачах можно использовать только что рассмотренную схему решения. Она, кстати, весьма напоминает алгоритм проверки векторов на коллинеарность, который мы рассматривали на уроке Понятие линейной (не) зависимости векторов. Базис векторов. Но существует более цивилизованная упаковка: Пример 1 Выяснить взаимное расположение прямых: Решение основано на исследовании направляющих векторов прямых: а) Из уравнений Вычислим определитель, составленный из координат данных векторов: На всякий случай поставлю на распутье камень с указателями: 1) Если мало что понятно, начните со статьи Векторы для чайников. Остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =) б) Найдем направляющие векторы прямых Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо. Очевидно, что коэффициенты при неизвестных Выясним, справедливо ли равенство Таким образом, в) Найдем направляющие векторы прямых Вычислим определитель, составленный из координат данных векторов: Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов Теперь выясним, справедливо ли равенство Полученное значение Таким образом, прямые совпадают. Ответ: Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно буквально в считанные секунды. В этой связи не вижу смысла предлагать что-либо для самостоятельного решения, лучше заложим ещё один важный кирпич в геометрический фундамент:
|

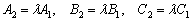
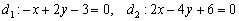 и составим три уравнения из соответствующих коэффициентов:
и составим три уравнения из соответствующих коэффициентов:  . Из каждого уравнения следует, что
. Из каждого уравнения следует, что  , следовательно, данные прямые совпадают.
, следовательно, данные прямые совпадают. умножить на –1 (сменить знаки), и все коэффициенты уравнения
умножить на –1 (сменить знаки), и все коэффициенты уравнения 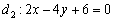 сократить на 2, то получится одно и то же уравнение:
сократить на 2, то получится одно и то же уравнение: 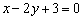 .
. пропорциональны:
пропорциональны:  , но
, но  .
. . Проверяем пропорциональность соответствующих коэффициентов при переменных
. Проверяем пропорциональность соответствующих коэффициентов при переменных 
 .
.
 составим систему:
составим систему:
 , а из второго уравнения:
, а из второго уравнения:  , значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных
, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных 
 найдём направляющие векторы прямых:
найдём направляющие векторы прямых:  .
. , значит, векторы
, значит, векторы  не коллинеарны и прямые
не коллинеарны и прямые  пересекаются.
пересекаются. :
:
 .
. :
:

 :
:
 , следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают. . Впрочем, можно и через коэффициенты самих уравнений:
. Впрочем, можно и через коэффициенты самих уравнений:  .
.
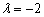 удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).



