Скалярное произведение 2-х векторов и его свойства
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов То есть, для векторов Таким образом, мы имеем третье определение скалярного произведения. Покажем, что это определение эквивалентно первому. Сначала докажем равенства Отложим от начала координат (точка О) векторы Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов мы можем записать Вспомнив формулу вычисления длины вектора по координатам, получаем Абсолютно аналогично доказывается справедливость равенств Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости
|
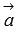и 
.
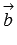на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид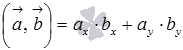
,
в трехмерном пространстве скалярное произведение в координатах находится как
.
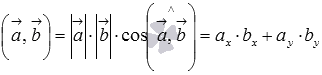для векторов 
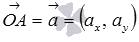и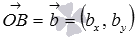 
. Тогда 
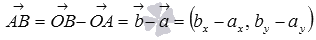(при необходимости обращайтесь к статьям операции над векторами и их свойства и операции над векторами в координатах).
. Так как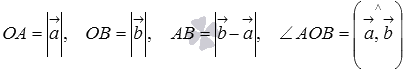 
, то последнее равенство можно переписать как 
, а по первому определению скалярного произведения имеем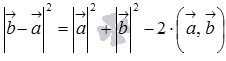 
, откуда 
.
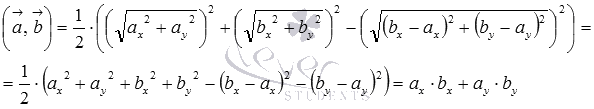
для векторов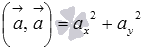 
, в пространстве 
.
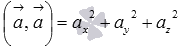