Решение. Поменяем местами первую и вторую строки матрицы А, так как элемент a1 1 равен нулю, а элемент a2 1 отличен от нуля:Поменяем местами первую и вторую строки матрицы А, так как элемент a1 1 равен нулю, а элемент a2 1 отличен от нуля:
В полученной матрице элемент
Так первый столбец преобразован к нужному виду. Элемент
Второй столбец полученной матрицы имеет нужный вид, так как элемент Так как
Умножим третью строку полученной матрицы на
На этом заканчиваем преобразования. Получаем Rank(A(5)) = 3, следовательно, Rank(A) = 3. Ответ: ранг исходной матрицы равен трем.
Подведем итог. Мы разобрали понятие ранга матрицы и рассмотрели три способа его нахождения:
Целесообразно всегда использовать метод элементарных преобразований при нахождении ранга матрицы, так как он приводит к результату при меньшем объеме вычислений, по сравнению с методом окаймляющих миноров, и тем более в сравнении с методом перебора всех миноров матрицы.
|
равен единице, поэтому не нужно производить умножение элементов первой строки на 
. Сделаем все элементы первого столбца, кроме первого, нулевыми: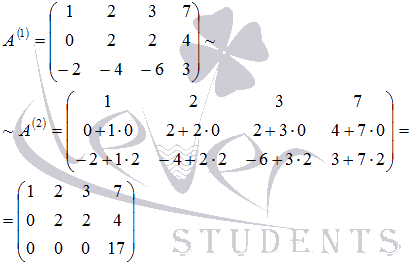
в полученной матрице отличен от нуля. Умножим элементы второй строки на 
:
уже равен нулю.
, а 
, то поменяем местами третий и четвертый столбцы:
:
