Система линейных уравнений имеет вид:
a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1,
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.1)
............
a m1 x 1 + a m1 x 2 +... + a mn x n = b m.
Здесь а i j и b i (i = 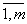 ; j =
; j =  ) - заданные, а x j - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:
) - заданные, а x j - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:
AX = B, (5.2)
где A = (а i j) - матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называется матрицей системы, X = (x 1, x 2,..., x n) T,
B = (b 1, b 2,..., b m) T - векторы-столбцы, составленные соответственно из неизвестных x j и из свободных членов b i.
Упорядоченная совокупность n вещественных чисел (c 1, c 2,..., c n) называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных x 1, x 2,..., x n каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c 1, c 2,..., c n) T такой, что AC B.
Система (5.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
Матрица
 ,
,
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.
Вопрос о совместности системы (5.1) решается следующей теоремой.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и A совпадают, т.е.
r(A) = r(` A) = r.
Для множества М решений системы (5.1) имеются три возможности:
1) M = (в этом случае система несовместна);
2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);
3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.
Система имеет единственное решение только в том случае, когда
r(A) = n. При этом число уравнений - не меньше числа неизвестных (m n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1,
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.3)
..................
a n1 x 1 + a n1 x 2 +... + a nn x n = b n.
Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера;
3) матричным методом.
Пример 2.12. Исследовать систему уравнений и решить ее, если она совместна:
5x 1 - x 2 + 2x 3 + x 4 = 7,
2x 1 + x 2 + 4x 3 - 2x 4 = 1,
x 1 - 3x 2 - 6x 3 + 5x 4 = 0.
Решение. Выписываем расширенную матрицу системы:
 .
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу  = 7 0; содержащие его миноры третьего порядка равны нулю:
= 7 0; содержащие его миноры третьего порядка равны нулю:

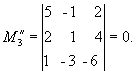
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A) = 2. Для вычисления ранга расширенной матрицы A рассмотрим окаймляющий минор
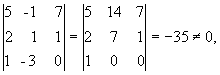
значит, ранг расширенной матрицы r(` A) = 3. Поскольку r(A) r(A), то система несовместна.
22.метод жордана гауса. Метод Гаусса — Жордана используется для решения систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь Гаусса и Жордана. Алгоритм: 1Выбирается первая колонка слева, в которой есть хоть одно отличное от нуля значение. 2Если самое верхнее число в этой колонке есть нуль, то меняется вся первая строка матрицы с другой строкой матрицы, где в этой колонке нет нуля. 3Все элементы первой строки делятся на верхний элемент выбранной колонки. 4Из оставшихся строк вычитается первая строка, умноженная на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) нуль. 5Далее проводим такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца. 6После повторения этой процедуры n-1 раз получаем верхнюю треугольную матрицу.7Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали. 8Повторяем предыдущий шаг для последующих строк. В итоге получаем единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования). Метод Гаусса-Жордана отличается от метода Гаусса тем, что при выполнении вычислений прямого хода на k- м шаге делим k- е уравнение на a (k- 1) kk (не равное 0) и выполняем дальнейшие вычисления с ведущим элементом, равным единице.Тогда в конце прямого хода имеем

а в конце обратного хода —
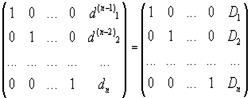
и тогда очевидно последний столбец содержит решение системы.
23.матем модель Леонтьева. В общем виде модель можно определить как условный образ (упрощенное изображение) реального объекта (процесса), который создается для более глубокого изучения действительности. Метод исследования, базирующийся на разработке и использовании моделей, называется моделированием. Необходимость моделирования обусловлена сложностью, а порой и невозможностью прямого изучения реального объекта (процесса). Значительно доступнее создавать и изучать прообразы реальных объектов (процессов), т.е. модели. Можно сказать, что теоретическое знание о чем-либо, как правило, представляет собой совокупность различных моделей. Эти модели отражают существенные свойства реального объекта (процесса), хотя на самом деле действительность значительно содержательнее и богаче. Подобие между моделируемым объектом и моделью может быть физическое, структурное, функциональное, динамическое, вероятностное и геометрическое. При физическом подобии объект и модель имеют одинаковую или сходную физическую природу. Структурное подобие предполагает наличие сходства между структурой объекта и структурой модели. При выполнении объектом и моделью под определенным воздействием сходных функций наблюдается функциональное подобие. При наблюдении за последовательно изменяющимися состояниями объекта и модели отмечается динамическое подобие, вероятностное подобие при наличии сходства между процессами вероятностного характера в объекте и модели, а геометрическое подобие при сходстве пространственных характеристик объекта и модели. Экономико-математические модели отражают наиболее существенные свойства реального объекта или процесса с помощью системы уравнений. Важнейшие виды балансовых моделей:1 частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей;2. межотраслевые балансы;3 матричные техпромфинпланы предприятий и фирм.
Графическая модель создается в виде рисунка, географической карты или чертежа. Например, зависимость между ценой и спросом может быть выражена в виде графика, на оси ординат которого отложен спрос (D), а на оси абсцисс цена (Р). Кривая нам наглядно иллюстрирует, что с ростом цены спрос падает, и наоборот. Конечно, данную зависимость можно выразить и словесно, но графически она намного нагляднее. 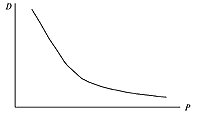
24.однород сист лин урав.фундаментальная система решений. Для того чтобы система имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных. Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю. Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений. Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.Алгоритм решения систем линейных однородных уравнений.1Находим ранг матрицы. 2Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные. 3Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре). 4Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля. 5Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные. 6Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы. 7В случае rang = n имеем тривиальное решение. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ. Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений. линейной однородной системы обыкновенных дифференциальных уравнений - базис векторного пространства действительных (комплексных) решений этой системы. (Система может состоять и из одного уравнения.) Более подробно это определение формулируется следующим образом.
Множество действительных (комплексных) решений {x1(t) ,...,xn (t)}(заданных на нек-ром множестве Е)линейной однородной системы обыкновенных дифференциальных уравнений наз. Ф. с. р. этой системы уравнений (на множестве Е)при выполнении совокупности следующих двух условий: 1) если действительные (комплексные) числа С 1,..., С n таковы, что функция C1x1(t) +...+Cnxn (t)тождественно равна нулю на Е, то все числа С 1,..., С n равны нулю; 2) для всякого действительного (комплексного) решения х(t)рассматриваемой системы уравнений найдутся действительные (соответственно комплексные) числа С 1,..., С n (не зависящие от t)такие, что x(t) = C 1x1(t) +...+Cnxn (t)при всех 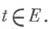
25.n- мерное пространство.векторн произв векторов и его свойства. ВЕКТОРНОЕ ПРОСТРАНСТВО матем. понятие, обобщающее понятие совокупности всех
(свободных) векторов обычного трёхмерного пространства. Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действит. числа (см. Векторное исчисление). В применении к любым векторам. x, у, zи любым числам альфа, бетаэти правила удовлетворяют след, условиям (условия А): 1) х+у=у+х (перестановочность сложения); 2) (x+y)+z=x+(y+z)
(ассоциативность сложения); 3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условиюx + 0=x для
любого вектора х; 4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0; 5) 1*х=х;) 
(ассоциативность умножения); 7) 
(распределит, свойство относительно числового множителя); 8) 
(распределит, свойство относительно векторного множителя). Векторным (или линейным) пространством наз. множество R, состоящее из элементов любой природы (называемых векторами), в к-ром определены операции сложения
элементов и умножения элементов на действит. числа, удовлетворяющие условиям А (условия 1-3 выражают, что операция сложения, определённая в В. п., превращает
его в коммутативную группу). Определение. Суммой векторов  и
и  называется вектор
называется вектор  , т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5). Определение. Произведением вектора
, т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5). Определение. Произведением вектора  на число
на число  называется вектор
называется вектор 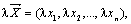 т.е. при умножении вектора на число каждая его координата умножается на это число.
т.е. при умножении вектора на число каждая его координата умножается на это число.
Можно проверить, что введенные таким образом операции над векторами удовлетворяют всем свойствам операций в линейном пространстве. Следовательно, арифметическое n -мерное пространство R n является частным случаем введенного ранее линейного пространства. Определение. Скалярным произведением двух векторов  и
и 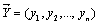 называется число, равное сумме произведений соответствующих координат векторов:
называется число, равное сумме произведений соответствующих координат векторов: 
Пример: Пусть  и
и  Определение. Два вектора называются ортогональными, если их скалярное произведение равно 0, т.е.
Определение. Два вектора называются ортогональными, если их скалярное произведение равно 0, т.е.  Определение. Линейное пространство с введенным скалярным произведением называется евклидовым n -мерным пространством.
Определение. Линейное пространство с введенным скалярным произведением называется евклидовым n -мерным пространством.
26.смешанное произведение векторов и его свойства. смешанным произведением трёх векторов  называют число, равное
называют число, равное  . Обозначается
. Обозначается  . Здесь первые два вектора умножаются векторно и затем полученный вектор
. Здесь первые два вектора умножаются векторно и затем полученный вектор  умножается скалярно на третий вектор
умножается скалярно на третий вектор  . Очевидно, такое произведение есть некоторое число. Рассмотрим свойства смешанного произведения.1 Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е.
. Очевидно, такое произведение есть некоторое число. Рассмотрим свойства смешанного произведения.1 Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. 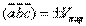 .2 Для любых векторов
.2 Для любых векторов  ,
,  ,
, 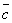 справедливо равенство-
справедливо равенство-
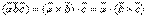 3 При перестановке любых двух сомножителей смешанноепроизведение меняет знак. Действительно, если рассмотрим смешанное произведение
3 При перестановке любых двух сомножителей смешанноепроизведение меняет знак. Действительно, если рассмотрим смешанное произведение  ,то,например,
,то,например,  или
или  .4 Смешанное произведение
.4 Смешанное произведение  тогда и только тогда, когда один из сомножителей равен нулю или векторы
тогда и только тогда, когда один из сомножителей равен нулю или векторы 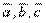 – компланарны. Т. о., смешанное произведение
– компланарны. Т. о., смешанное произведение  равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.
равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.
27.линейно зависимые и линейно не зависимые системы векторов. линейной комбинацией данных векторов называется любой вектор вида  , где
, где 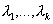 - некоторые числа. Числа
- некоторые числа. Числа 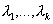 называются коэффициентами линейной комбинации. Говорят также, что в этом случае
называются коэффициентами линейной комбинации. Говорят также, что в этом случае  линейно выражается через данные векторы
линейно выражается через данные векторы  , т.е. получается из них с помощью линейных действий. Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Доказательство:1 Действительно, пусть имеем два коллинеарных вектора
, т.е. получается из них с помощью линейных действий. Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Доказательство:1 Действительно, пусть имеем два коллинеарных вектора  и
и  . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация
. Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация  при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например,
при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например,  . Но отсюда
. Но отсюда  , а это и означает линейную зависимость векторов
, а это и означает линейную зависимость векторов  и
и  .2 Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы
.2 Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы  и
и  линейно зависимы. Тогда найдутся числа λ1 и λ2 такие, что
линейно зависимы. Тогда найдутся числа λ1 и λ2 такие, что  , причём, например, λ2 ≠ 0. Тогда
, причём, например, λ2 ≠ 0. Тогда  , т.е. векторы коллинеарны. Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны. Аналогично можно доказать следующую теорему. Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. Доказательство. 1 Пусть три вектора
, т.е. векторы коллинеарны. Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны. Аналогично можно доказать следующую теорему. Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. Доказательство. 1 Пусть три вектора  линейно зависимы, т.е.
линейно зависимы, т.е.  , где, например, λ3 ≠ 0. Тогда
, где, например, λ3 ≠ 0. Тогда  .2 Отнесём векторы
.2 Отнесём векторы  и
и  к одному началу и проведём через них плоскость. Тогда
к одному началу и проведём через них плоскость. Тогда  и
и  будут лежать в той же плоскости, а потому и их сумма, т.е.
будут лежать в той же плоскости, а потому и их сумма, т.е. 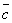 будет лежать в той же плоскости, т.е.
будет лежать в той же плоскости, т.е.  – компланарны.2 Пусть теперь векторы
– компланарны.2 Пусть теперь векторы  – компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу. Если векторы
– компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу. Если векторы  и
и  не коллинеарны, то очевидно, вектор
не коллинеарны, то очевидно, вектор 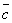 можно предствить в виде
можно предствить в виде  . Действительно из рисунка видно, что
. Действительно из рисунка видно, что  , где
, где 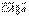 и
и  , а значит найдутся числа
, а значит найдутся числа 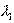 и
и  такие, что
такие, что  . Если же вектор
. Если же вектор  коллинеарен вектору
коллинеарен вектору  , то один из них линейно выражен через другой, т.е.
, то один из них линейно выражен через другой, т.е. 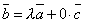 . Что и требовалось доказать.
. Что и требовалось доказать.
28. базис пространства. Разложение вектора по произвольному базису. Определение. Базисом в пространстве Rn называется любая система из n -линейно независимых векторов. Каждый вектор из Rn, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.
Пусть 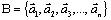 – базис пространства Rn и
– базис пространства Rn и  . Тогда найдутся такие числа λ1, λ2, …, λn, что
. Тогда найдутся такие числа λ1, λ2, …, λn, что  .
.
Коэффициенты разложения λ1, λ2, …, λn, называются координатами вектора  в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
Пример. Доказать, что векторы  образуют базис в R3.
образуют базис в R3.
Решение. Покажем, что равенство 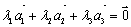 возможно только при λ1 = λ2 = λ3 =0:
возможно только при λ1 = λ2 = λ3 =0:

или 
Решив систему, получим λ1=0, λ2=0, λ3=0. Так как все λ i =0 (i =1,2,3), то  - линейно независимы. Они могут составить базис в R3.
- линейно независимы. Они могут составить базис в R3.
Очевидно, любой новый набор из векторов 

 может тоже быть взятым в качестве базиса в R3. Итак, базис может быть выбран неединственным образом.
может тоже быть взятым в качестве базиса в R3. Итак, базис может быть выбран неединственным образом.
Пример. Разложить вектор  по базису
по базису  .
.
Решение.  . Подставим координаты всех векторов и выполним действия над ними:
. Подставим координаты всех векторов и выполним действия над ними:

Приравняв координаты, получим систему уравнений:

Решим ее:  .
.
Таким образом, получим разложение:  .
.
В базисе  вектор
вектор  имеет координаты
имеет координаты  .
.
Замечание. В каждом n -мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе.

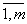 ; j =
; j =  ) - заданные, а x j - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:
) - заданные, а x j - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде: ,
, .
. = 7 0; содержащие его миноры третьего порядка равны нулю:
= 7 0; содержащие его миноры третьего порядка равны нулю:
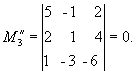
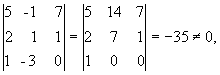

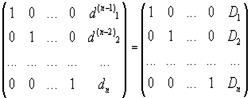

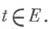



 и
и  называется вектор
называется вектор  , т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5). Определение. Произведением вектора
, т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5). Определение. Произведением вектора  на число
на число  называется вектор
называется вектор 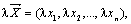 т.е. при умножении вектора на число каждая его координата умножается на это число.
т.е. при умножении вектора на число каждая его координата умножается на это число. и
и 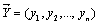 называется число, равное сумме произведений соответствующих координат векторов:
называется число, равное сумме произведений соответствующих координат векторов: 
 и
и  Определение. Два вектора называются ортогональными, если их скалярное произведение равно 0, т.е.
Определение. Два вектора называются ортогональными, если их скалярное произведение равно 0, т.е.  Определение. Линейное пространство с введенным скалярным произведением называется евклидовым n -мерным пространством.
Определение. Линейное пространство с введенным скалярным произведением называется евклидовым n -мерным пространством. называют число, равное
называют число, равное  . Обозначается
. Обозначается  . Здесь первые два вектора умножаются векторно и затем полученный вектор
. Здесь первые два вектора умножаются векторно и затем полученный вектор  умножается скалярно на третий вектор
умножается скалярно на третий вектор  . Очевидно, такое произведение есть некоторое число. Рассмотрим свойства смешанного произведения.1 Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е.
. Очевидно, такое произведение есть некоторое число. Рассмотрим свойства смешанного произведения.1 Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. 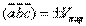 .2 Для любых векторов
.2 Для любых векторов  ,
,  ,
, 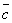 справедливо равенство-
справедливо равенство-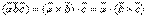 3 При перестановке любых двух сомножителей смешанноепроизведение меняет знак. Действительно, если рассмотрим смешанное произведение
3 При перестановке любых двух сомножителей смешанноепроизведение меняет знак. Действительно, если рассмотрим смешанное произведение  ,то,например,
,то,например,  или
или  .4 Смешанное произведение
.4 Смешанное произведение  тогда и только тогда, когда один из сомножителей равен нулю или векторы
тогда и только тогда, когда один из сомножителей равен нулю или векторы 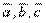 – компланарны. Т. о., смешанное произведение
– компланарны. Т. о., смешанное произведение  равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.
равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора. , где
, где 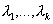 - некоторые числа. Числа
- некоторые числа. Числа  , т.е. получается из них с помощью линейных действий. Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Доказательство:1 Действительно, пусть имеем два коллинеарных вектора
, т.е. получается из них с помощью линейных действий. Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Доказательство:1 Действительно, пусть имеем два коллинеарных вектора  при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например,
при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например,  . Но отсюда
. Но отсюда  , а это и означает линейную зависимость векторов
, а это и означает линейную зависимость векторов  , т.е. векторы коллинеарны. Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны. Аналогично можно доказать следующую теорему. Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. Доказательство. 1 Пусть три вектора
, т.е. векторы коллинеарны. Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны. Аналогично можно доказать следующую теорему. Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. Доказательство. 1 Пусть три вектора  линейно зависимы, т.е.
линейно зависимы, т.е.  , где, например, λ3 ≠ 0. Тогда
, где, например, λ3 ≠ 0. Тогда  .2 Отнесём векторы
.2 Отнесём векторы  и
и  будут лежать в той же плоскости, а потому и их сумма, т.е.
будут лежать в той же плоскости, а потому и их сумма, т.е.  – компланарны.2 Пусть теперь векторы
– компланарны.2 Пусть теперь векторы  . Действительно из рисунка видно, что
. Действительно из рисунка видно, что  , где
, где 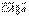 и
и  , а значит найдутся числа
, а значит найдутся числа 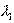 и
и  такие, что
такие, что  . Если же вектор
. Если же вектор 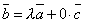 . Что и требовалось доказать.
. Что и требовалось доказать.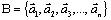 – базис пространства Rn и
– базис пространства Rn и  . Тогда найдутся такие числа λ1, λ2, …, λn, что
. Тогда найдутся такие числа λ1, λ2, …, λn, что  .
. в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно. образуют базис в R3.
образуют базис в R3.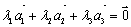 возможно только при λ1 = λ2 = λ3 =0:
возможно только при λ1 = λ2 = λ3 =0:

 - линейно независимы. Они могут составить базис в R3.
- линейно независимы. Они могут составить базис в R3.

 может тоже быть взятым в качестве базиса в R3. Итак, базис может быть выбран неединственным образом.
может тоже быть взятым в качестве базиса в R3. Итак, базис может быть выбран неединственным образом. по базису
по базису  .
. . Подставим координаты всех векторов и выполним действия над ними:
. Подставим координаты всех векторов и выполним действия над ними:

 .
. .
. вектор
вектор  .
.


