Основные определения и обозначения.
Рассмотрим систему из p линейных уравнений с n неизвестными (p может быть равно n):
где Если Совокупность значения неизвестных переменных Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется совместной, в противном случае – несовместной. Если СЛАУ имеет единственное решение, то она называется определенной. Если решений больше одного, то система называется неопределенной. Говорят, что система записана в координатной форме, если она имеет вид
Эта система в матричной форме записи имеет вид Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,
Квадратная матрица А называется вырожденной, если ее определитель равен нулю. Если
Следует оговорить следующий момент. Если с системой линейных алгебраических уравнений
то получится эквивалентная система, которая имеет такие же решения (или также как и исходная не имеет решений).
Теперь можно переходить к описанию метода Гаусса.
|


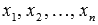 - неизвестные переменные,
- неизвестные переменные,  - числа (действительные или комплексные),
- числа (действительные или комплексные), 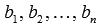 - свободные члены.
- свободные члены. , то система линейных алгебраических уравнений называется однородной, в противном случае – неоднородной.
, то система линейных алгебраических уравнений называется однородной, в противном случае – неоднородной. , при которых все уравнения системы обращаются в тождества, называется решением СЛАУ.
, при которых все уравнения системы обращаются в тождества, называется решением СЛАУ.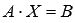 , где
, где  - основная матрица СЛАУ,
- основная матрица СЛАУ,  - матрица столбец неизвестных переменных,
- матрица столбец неизвестных переменных,  - матрица свободных членов.
- матрица свободных членов.
 , то матрица А называется невырожденной.
, то матрица А называется невырожденной.


