Разность матриц A и B будем обозначать A-B.
Произведением матрицы Произведение матрицы A на число Теорема 2.2 Операция умножения матрицы на число обладает следующими свойствами: 1) 2) 3) 4) 5) -A=(-1)A. Все перечисленные свойства непосредственно вытекают из определения. Операции сложения матриц и умножения матрицы на число позволяют для произвольных матриц Умножение матриц. Произведением матриц
Произведение матриц A и B будем обозначать C=AB. Из определения следует, что произведение AB определено лишь в том случае, когда число столбцов матрицы A совпадает с числом строк матрицы B. Это означает, что оба произведения AB и BA определены тогда и только тогда, когда матрицы A и B имеют размеры Матрицы A и B называются перестановочными или коммутирующими, если AB=BA. Теорема 2.3 Операция умножения матриц обладает следующими свойствами: 1) (AB)C=A(BC); (Свойство ассоциативности) 2) 3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C, для которых левые части равенств имеют смысл. Справедливость свойств 2) и 3) доказываются непосредственно. В качестве иллюстрации приведём доказательство первого равенства свойства 3). Пусть
Из равенств (1) и (2) следует, что Подробное доказательство свойства 1) можно найти в учебнике В. А. Ильин, Г. Д. Ким "Линейная алгебра и аналитическая геометрия". Заметим, что для любой матрицы
Транспонирование матриц. Пусть Транспонированная матрица также обозначается символами Заметим, что при транспонировании матрицы её строки становятся столбцами матрицы Теорема 2.4. Операция транспонирования матриц обладает следующими свойствами: 1) 2) 3) 4) Свойства 1), 2), 4) непосредственно вытекают из определения. Приведём доказательство свойства 3). Пусть
что доказывает справедливость свойства 3).
|

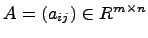 на число
на число  называется матрица
называется матрица 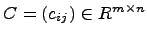 , элементы которой определены равенством
, элементы которой определены равенством 
 .
.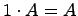 ;
;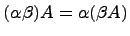 ;
; (Распределительное свойство относительно сложения матриц);
(Распределительное свойство относительно сложения матриц); (Распределительное свойство относительно сложения чисел);
(Распределительное свойство относительно сложения чисел);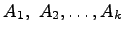 одинакового размера
одинакового размера  и произвольных чисел
и произвольных чисел  однозначно определить матрицу
однозначно определить матрицу  , называемую линейной комбинацией матриц
, называемую линейной комбинацией матриц  называется матрица
называется матрица  , элементы которой определены равенством
, элементы которой определены равенством
 соответственно. Следовательно равенство AB=BA возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.
соответственно. Следовательно равенство AB=BA возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.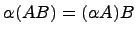 , для любого действительного числа
, для любого действительного числа  ,
, 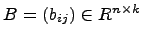 ,
,  . Матрицы A(B+C) и AB+AC имеют одинаковый размер -
. Матрицы A(B+C) и AB+AC имеют одинаковый размер - 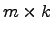 . Пусть
. Пусть  - элемент матрицы A(B+C) в позиции (i,j),
- элемент матрицы A(B+C) в позиции (i,j),  - элемент матрицы AB+AC в позиции (i,j), тогда
- элемент матрицы AB+AC в позиции (i,j), тогда

 , что доказывает первое равенство свойства 3).
, что доказывает первое равенство свойства 3).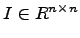 и
и  справедливо:
справедливо:
 называется транспонированной к матрице A, если
называется транспонированной к матрице A, если 
 и
и  .
. , с теми же номерами, а столбцы - строками.
, с теми же номерами, а столбцы - строками. ;
; , для любого действительного числа
, для любого действительного числа  ;
; , для любых матриц A и B, для которых имеют смысл левые части равенств.
, для любых матриц A и B, для которых имеют смысл левые части равенств.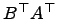 существуют, при этом размеры
существуют, при этом размеры  и
и  . Пусть
. Пусть  - элемент матрицы
- элемент матрицы 



